הרצאה 10 - Neural Networks
רשת נוירונים מלאכותית כמודל פרמטרי
נתקלנו במספר מקרים בהם ניסינו למצוא פונקציה שתבצע פעולה או תתאר תופעה כלשהי (מציאת חזאי או פונקציית פילוג).
דרך נוחה לעשות זאת היא בעזרת מודל פרמטרי ומציאת הפרמטרים האופטימאלים.
עד כה עבדנו עם מודלים לינאריים בפרמטרים.
ניתן לקרב הרבה מאד פונקציות בעזרת פולינום מסדר מספיק גבוה.
מודלים אלו הם לא מאד מוצלחים ובעייתיים וכאשר x \boldsymbol{x} x
האם ישנם מודלים מתאימים יותר?
רשתות נוירונים מלאכותיות
בשנים האחרונות מודלים אלו הוכיחו את עצמם כמודלים פרמטריים מאד יעילים לפתרון מגוון רחב של בעיות.
הההשראה לצורה שבה הם בנויים מגיעה מרשתות עצביות ביולוגיות.
רשתות עצביות ביולוגיות
תקשורת בין תאי עצב
רשתות עצביות ביולוגיות
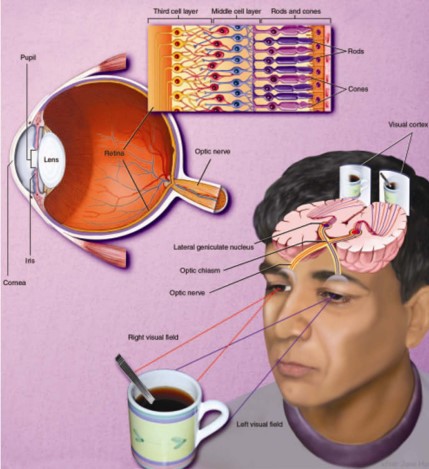
מפוטונים לזיהוי אובייקטים במרחב
נוירון ביולוגי
בצורה פשטנית ניתן לתאר את האופן בו נוירון ביולוגי פועל כך:
נוירון ביולוגי
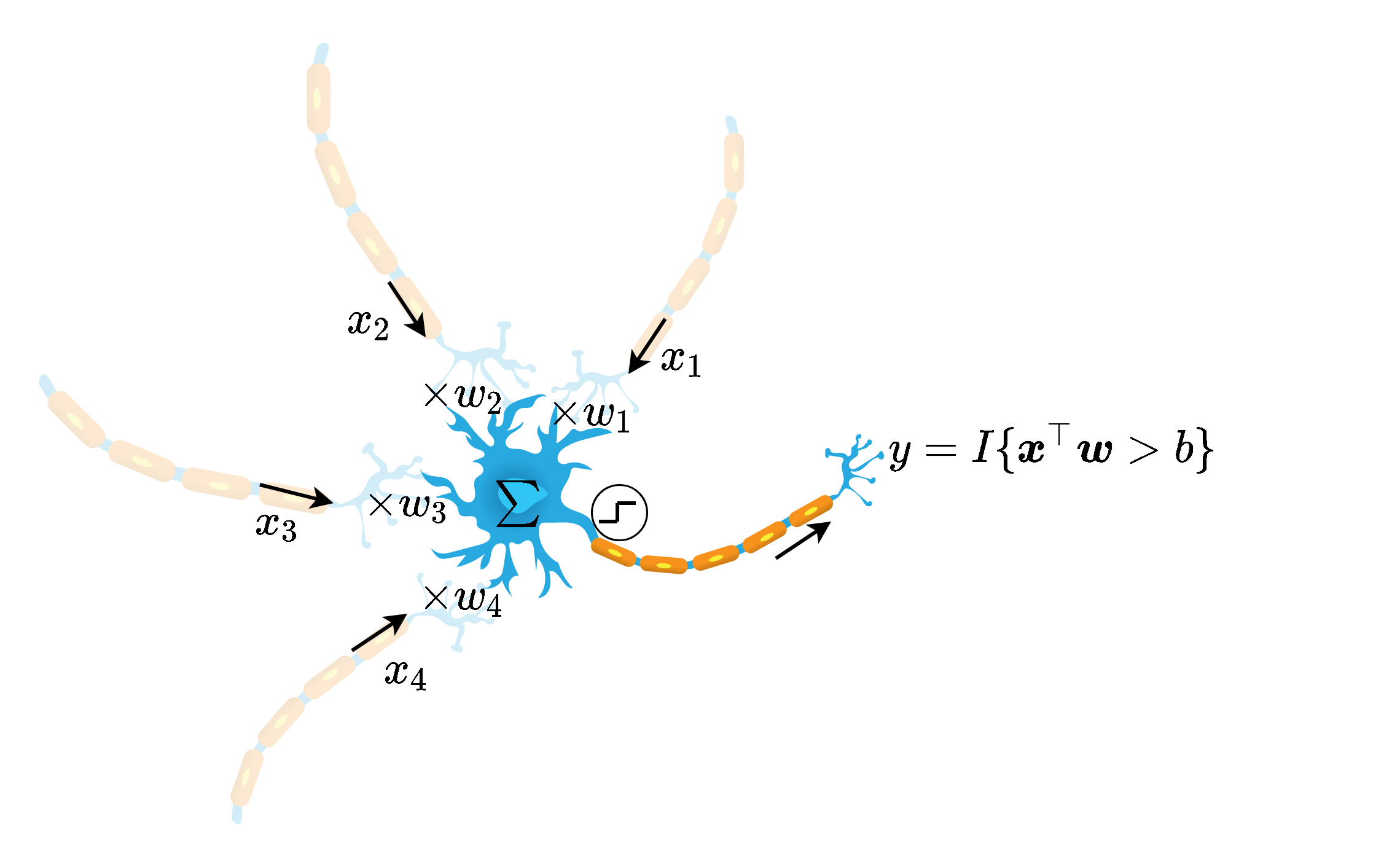
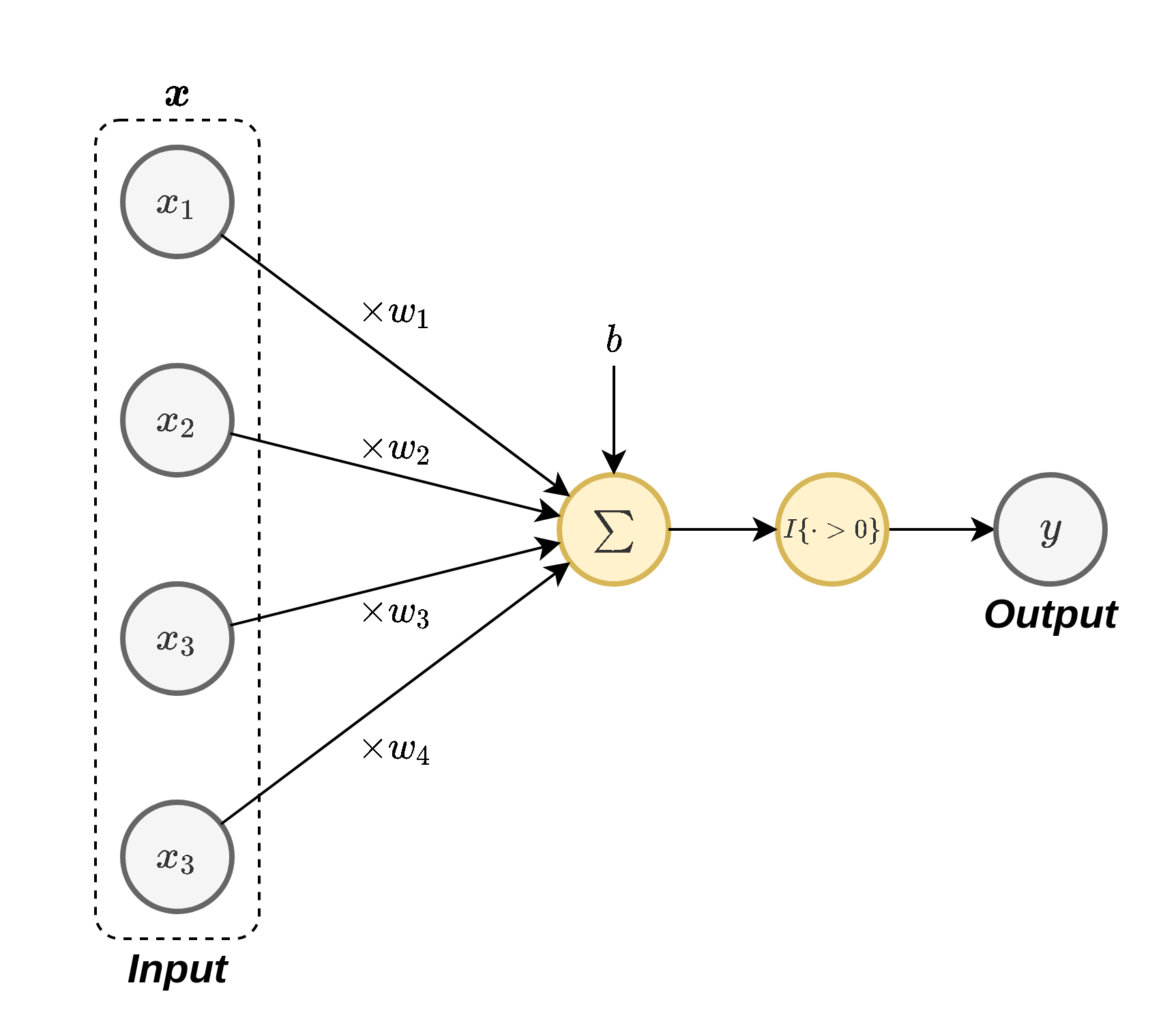
באופן סכימתי ניתן למדל את פעולת הנוירון באופן הבא:
y = I { x ⊤ w + b > 0 } y=I\{\boldsymbol{x}^{\top}\boldsymbol{w}+b>0\} y = I { x ⊤ w + b > 0 }
נוירונים ברשת נוירונים מלאכותית
נוירונים ברשת נוירונים מלאכותית
באופן סכימתי נסמן נוירון בודד באופן הבא:
רשת נוירונים
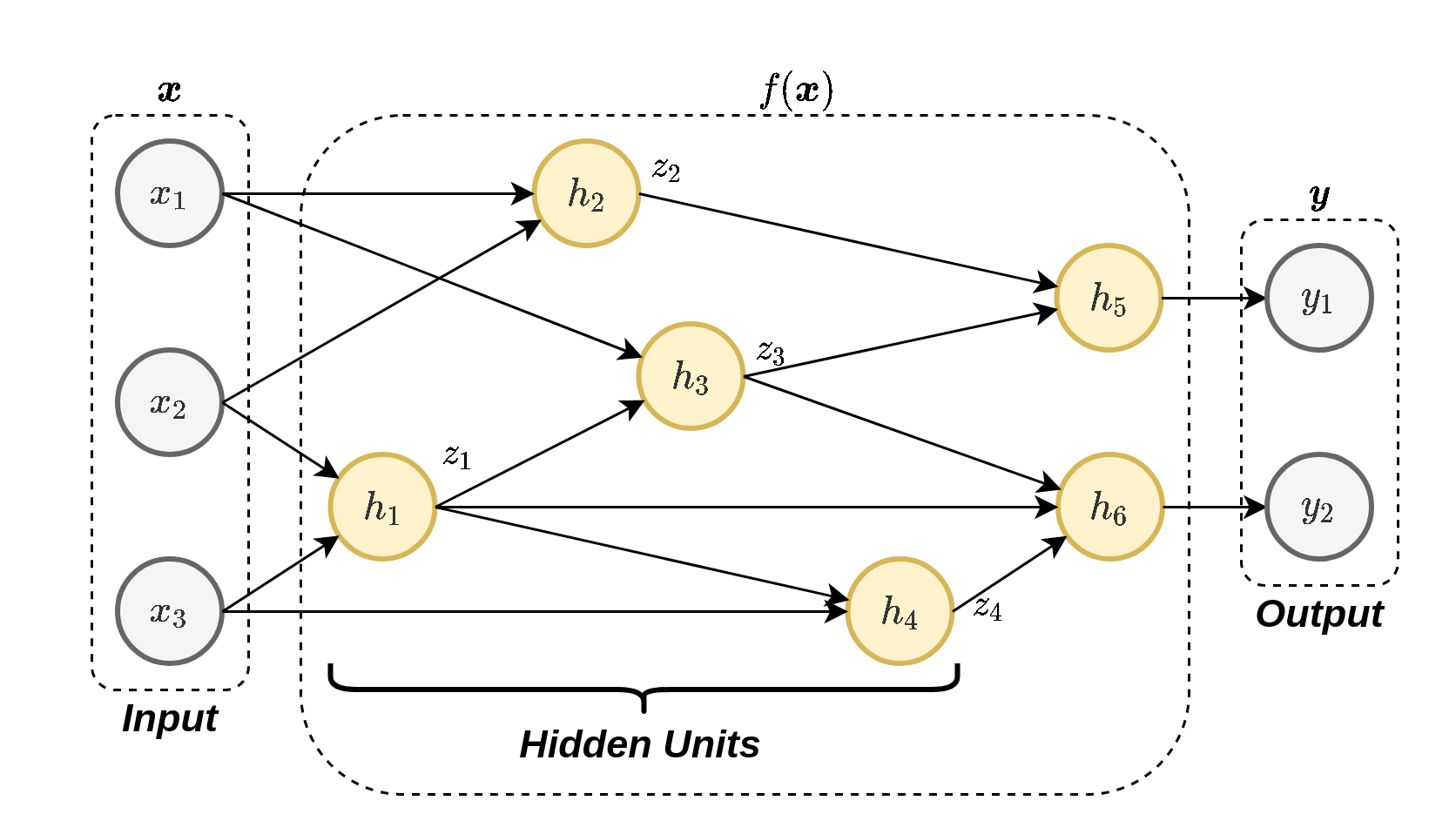
נשלב מספר נוירונים יחד על מנת לבנות רשת נוירונים:
רשת שכזו יכולה לקרב מגוון מאד רחב של פונקציות. הפרמטרים של המודל יהיו הפרמטרים של כל הנוירונים.
רשת נוירונים
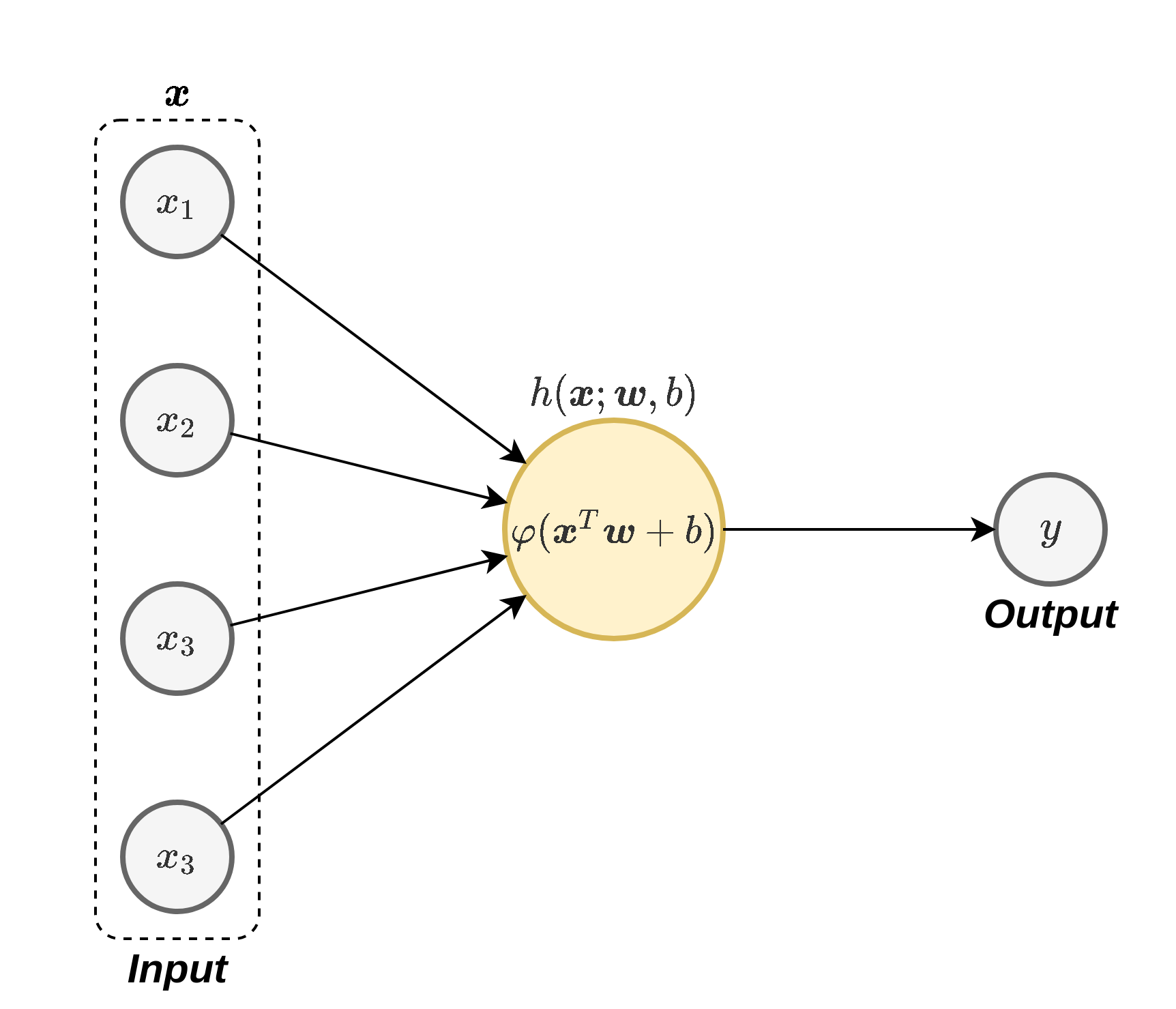
לרוב הנוירונים יהיו מהצורה של:
h j ( x ; w j , b j ) = φ ( x ⊤ w j + b j ) h_j(\boldsymbol{x};\boldsymbol{w}_j,b_j)=\varphi(\boldsymbol{x}^{\top}\boldsymbol{w}_j+b_j) h j ( x ; w j , b j ) = φ ( x ⊤ w j + b j ) אך ניתן גם לבחור פונקציות אחרות. בקורס זה, אלא אם נאמר אחרת, אנו נניח כי כי הנוירונים הם מהצורה הזו.
הארכיטקטורה של הרשת
המבנה של הרשת כולל את מספר הנוירונים שהיא מכילה ואת הדרך שבה הם מחוברים אחד לשני.
בחירת הארכיטקטורה היא קריטית לביצועים.
לשימושים שונים מתאימות ארכיטקטורות שונות.
חלק גדול מאד מהמחקר שנעשה כיום הוא סביב הנושא של חיפוש ארכיטקטורות.
התהליך של מציאת הארכיטקטורה דורש לא מעט ניסיון, אינטואיציה והרבה ניסוי וטעיה.
לרוב נמצא בעיה דומה ונשתמש בארכיטקטורה שעבדה טוב במקרה זה (נרפרנס).
הארכיטקטורה של הרשת
יחידות נסתרות (hidden units ): הנוירונים אשר אינם מחוברים למוצא הרשת.רשת עמוקה (deep network ): רשת אשר מכילה מסלולים אשר עוברים דרך יותר מיחידה נסתרת אחת.
Feed-forward vs. Recurrent
אנו מבדילים בין שני סוגי ארכיטקטורות:
רשת הזנה קדמית (feed-forward network) : ארכיטקטורות אשר אינן מכילות מסלולים מעגליים.רשתות נשנות (recurrent neural network - RNN) : בקורס זה לא נעסוק ברשתות מסוג זה. אלו ארכיטקטורות אשר כן מכילות מסלולים מעגליים.
על החשיבות של פונקציות ההפעלה
ללא פונקציית ההפעלה הנורונים היו לינאריים ולכן כל הרשת תהיה פשוט מודל לינארי.
המוצא של הרשת
Regression + ERM
הרשת תמדל חזאי אשר אמור להוציא סקלר שמקבל ערכים רציפים בתחום לא מוגבל.
אנו נרצה שהמוצא של הרשת יתנקז לנוירון בודד ללא פונקציית אקטיבציה כדי לקבל ערכים ממשיים ללא הגבלה.
המוצא של הרשת
סיווג בינארי דיסקרימינטיבי הסתברותי
הרשת תמדל את p y ∣ x ( 1 ∣ x ) p_{\text{y}|\mathbf{x}}(1|\boldsymbol{x}) p y ∣ x ( 1 ∣ x )
אנו נרצה שהרשת תוציא ערך סקלרי רציף בתחום בין 0 ל-1.
שהמוצא של הרשת יתנקז לנוירון בודד עם פונקציית הפעלה שמוציאה ערכים בתחום [ 0 , 1 ] [0,1] [ 0 , 1 ]
סיווג לא בינארי דיסקרימינטיבי הסתברותי
הרשת תמדל את כל ההסתברויות p y ∣ x ( y ∣ x ) p_{\text{y}|\mathbf{x}}(y|\boldsymbol{x}) p y ∣ x ( y ∣ x )
נרצה שהרשת תוציא וקטור באורך C C C
מציאת הפרמטרים של המודל
בעיית האופטימיזציה:
ב ERM אנו ננסה למזער את ה risk האמפירי.
בגישה הדיסקרימינטיבית ההסתברותית נשתמש ב MLE או MAP. במקרה של רגרסיה לוגיסטית נוכל להשתמש בפונקציה מהרצאה 9
כדי לפתור את בעיית האופטימיזציה נשתמש ב gradient descent.
מציאת הפרמטרים של המודל
נסמן את מוצא הרשת f ( x ; W ) ∈ R f(x;W)\in\mathbb{R} f ( x ; W ) ∈ R
רגרסיה: לדוגמה, פונקציית ההפסד של least squares היא
L ( W ) = ∑ i = 1 n ( y ( i ) − f ( x ( i ) ; W ) ) 2 \mathcal{L}(W)=\sum_{i=1}^{n}\left(y^{(i)}-f\left(x^{(i)};W\right)\right)^{2} L ( W ) = i = 1 ∑ n ( y ( i ) − f ( x ( i ) ; W ) ) 2 סיווג בינארי: במקרה של רגרסיה לוגיסטית ניתן להשתמש בפונקציה מהרצאה 9:
L ( W ) = − ∑ i = 1 N [ y ( i ) log ( σ ( f ( x ( i ) ; W ) ) ) + ( 1 − y ( i ) ) log ( 1 − σ ( f ( x ( i ) ; W ) ) ) ] \mathcal{L}(W)=-\sum_{i=1}^{N}\left[y^{(i)}\log\left(\sigma\left(f\left(x^{(i)};W\right)\right)\right)+\left(1-y^{(i)}\right)\log\left(1-\sigma\left(f\left(x^{(i)};W\right)\right)\right)\right] L ( W ) = − i = 1 ∑ N [ y ( i ) log ( σ ( f ( x ( i ) ; W ) ) ) + ( 1 − y ( i ) ) log ( 1 − σ ( f ( x ( i ) ; W ) ) ) ] עם פונקציית הסיגמואיד σ ( z ) = 1 / ( 1 + exp ( − z ) ) \sigma(z)=1/\left(1+\exp(-z)\right) σ ( z ) = 1 / ( 1 + exp ( − z ) )
במקרה של סיווג רב מחלקתי f ( x ; W ) = ( f 1 ( x ; W ) , … , f c ( x ; W ) ) ∈ R C f(x;W)=\left(f_{1}(x;W),\ldots,f_{c}(x;W)\right)\in\mathbb{R}^{C} f ( x ; W ) = ( f 1 ( x ; W ) , … , f c ( x ; W ) ) ∈ R C
MultiLayer Perceptron (MLP)
הנוירונים מסודרים בשכבות (layers), כשתייים או יותר
השכבות הן Fully Connected (FC) (כל נוירון מוזן מכל הנוירונים שבשכבה שלפני).
MultiLayer Perceptron (MLP)
מה שמגדיר את הארכיטקטורה במקרה של MLP הוא מספר השכבות הנסתרות וכמות הנוירונים בכל שכבה (רוחב השכבה ). בדוגמה הזו, יש ברשת 3 שכבות ברוחב 2, 3 ו 2.
רישום מטריצי
W i = [ − w i , 1 − − w i , 2 − ⋮ ] W_i=
\begin{bmatrix}
-&\boldsymbol{w}_{i,1}&-\\
-&\boldsymbol{w}_{i,2}&-\\
&\vdots&\\
\end{bmatrix} W i = ⎣ ⎢ ⎢ ⎡ − − w i , 1 w i , 2 ⋮ − − ⎦ ⎥ ⎥ ⎤ b i = [ b i , 1 , b i , 2 , … ] ⊤ \boldsymbol{b}_i=[b_{i,1},b_{i,2},\dots]^{\top} b i = [ b i , 1 , b i , 2 , … ] ⊤
כאשר W i , b i W_i, b_i W i , b i i i i i i i d i d_i d i d i n d_{in} d i n d o u t d_{out} d o u t
הפונקציה אותה מממשת השכבה כולה הינה:
z i = φ ( W i z i − 1 + b i ) \boldsymbol{z}_i=\varphi(W_i\boldsymbol{z}_{i-1}+\boldsymbol{b}_i) z i = φ ( W i z i − 1 + b i )
רישום מטריצי
עבור MLP כללי עם L L L
z L = φ L ( W L z L − 1 + b L ) = φ L ( W L φ L − 1 ( W L − 1 z L − 2 + b L − 1 ) ) = h L ∘ h L − 1 ∘ ⋯ ∘ h 1 ( x ) z_{L}=\varphi_{L}\left(W_{L}z_{L-1}+b_{L}\right)=\varphi_{L}\left(W_{L}\varphi_{L-1}\left(W_{L-1}z_{L-2}+b_{L-1}\right)\right)=h_{L}\circ h_{L-1}\circ\cdots\circ h_{1}(x) z L = φ L ( W L z L − 1 + b L ) = φ L ( W L φ L − 1 ( W L − 1 z L − 2 + b L − 1 ) ) = h L ∘ h L − 1 ∘ ⋯ ∘ h 1 ( x ) כאשר
h ℓ ( z ℓ − 1 ) = φ ℓ ( W ℓ z ℓ − 1 + b ℓ ) h_{\ell}\left(z_{\ell-1}\right)=\varphi_{\ell}\left(W_{\ell}z_{\ell-1}+b_{\ell}\right) h ℓ ( z ℓ − 1 ) = φ ℓ ( W ℓ z ℓ − 1 + b ℓ ) שימו לב, φ ℓ \varphi_{\ell} φ ℓ
ניתן לכתוב זאת בצורה רקורסיבית
z 0 = x u ℓ = W ℓ z l − 1 + b ℓ for l = 1 to L z ℓ = φ ℓ ( u ℓ ) for l = 1 to L \begin{aligned}\mathbf{z}_{0} & =\mathbf{x}\\
\mathbf{u}_{\ell} & =W_{\ell}\mathbf{z}_{l-1}+\mathbf{b}_{\ell}\quad\text{for }l=1\text{ to }L\\
\mathbf{z}_{\ell} & =\varphi_{\ell}(\mathbf{u}_{\ell})\quad\text{for }l=1\text{ to }L
\end{aligned} z 0 u ℓ z ℓ = x = W ℓ z l − 1 + b ℓ for l = 1 to L = φ ℓ ( u ℓ ) for l = 1 to L כאשר פעולת האקטיבציה φ ℓ \varphi_{\ell} φ ℓ y L = z L \mathbf{y}_{L}=\mathbf{z}_{L} y L = z L
"משפט הקירוב האוניברסלי"
בהינתן:
פונקציית הפעלה רציפה כלשהיא φ \varphi φ אינה פולינומיאלית .
ופונקציה רציפה כלשהיא על קוביית היחידה f : [ 0 , 1 ] D in → [ 0 , 1 ] D out f:[0,1]^{D_{\text{in}}}\rightarrow[0,1]^{D_{\text{out}}} f : [ 0 , 1 ] D in → [ 0 , 1 ] D out
אזי ניתן למצוא פונקציה f ε : [ 0 , 1 ] D in → [ 0 , 1 ] D out f_{\varepsilon}:[0,1]^{D_{\text{in}}}\rightarrow[0,1]^{D_{\text{out}}} f ε : [ 0 , 1 ] D in → [ 0 , 1 ] D out
f ε ( x ) = W 2 φ ( W 1 x + b 1 ) + b 2 f_{\varepsilon}(\boldsymbol{x})=W_2\varphi(W_1\boldsymbol{x}+\boldsymbol{b}_1)+\boldsymbol{b}_2 f ε ( x ) = W 2 φ ( W 1 x + b 1 ) + b 2 כך ש:
sup x ∈ [ 0 , 1 ] D in ∥ f ( x ) − f ε ( x ) ∥ < ε \underset{x\in[0,1]^{D_{\text{in}}}}{\text{sup}}\lVert
f(\boldsymbol{x})-f_{\varepsilon}(\boldsymbol{x})
\rVert<\varepsilon x ∈ [ 0 , 1 ] D in sup ∥ f ( x ) − f ε ( x ) ∥ < ε
הערה לגבי נגזרות וקטוריות
זכרו כי עבור פונקציה סקלרית f ( θ ) , θ ∈ R n f(\boldsymbol{\theta}),\boldsymbol{\theta}\in\mathbb{R}^{n} f ( θ ) , θ ∈ R n
∇ f ( θ ) = ∂ f ( θ ) ∂ θ = [ ∂ f ( θ ) ∂ θ 1 , … , ∂ f ( θ ) ∂ θ n ] ∈ R 1 × n \nabla f(\theta)=\frac{\partial f(\theta)}{\partial\theta}=\left[\frac{\partial f(\theta)}{\partial\theta_{1}},\ldots,\frac{\partial f(\theta)}{\partial\theta_{n}}\right]\in\mathbb{R}^{1\times n} ∇ f ( θ ) = ∂ θ ∂ f ( θ ) = [ ∂ θ 1 ∂ f ( θ ) , … , ∂ θ n ∂ f ( θ ) ] ∈ R 1 × n תהי g ( θ ) \boldsymbol{g}(\boldsymbol{\theta}) g ( θ ) θ \mathbf{\boldsymbol{\theta}} θ g : θ ↦ R m \mathbf{g}:\mathbf{\theta}\mapsto\mathbb{R}^{m} g : θ ↦ R m g ( θ ) = ( g 1 ( θ ) , … , g m ( θ ) ) \mathbf{g}(\mathbf{\boldsymbol{\theta}})=\left(g_{1}(\mathbf{\mathbf{\boldsymbol{\theta}}}),\ldots,g_{m}(\mathbf{\boldsymbol{\theta}})\right) g ( θ ) = ( g 1 ( θ ) , … , g m ( θ ) )
אזי
∂ g ( θ ) ∂ θ = [ ∂ g i ( θ ) ∂ θ j ] i j ∈ R m × n \frac{\partial\mathbf{g}(\boldsymbol{\theta})}{\partial\boldsymbol{\theta}}=\left[\frac{\partial g_{i}(\boldsymbol{\theta})}{\partial\theta_{j}}\right]_{ij}\in\mathbb{R}^{m\times n} ∂ θ ∂ g ( θ ) = [ ∂ θ j ∂ g i ( θ ) ] i j ∈ R m × n ובמקרה הפשוט בו g ( θ ) = ( g 1 ( θ 1 ) , … , g m ( θ m ) ) \mathbf{g}(\boldsymbol{\theta})=\left(g_{1}(\theta_{1}),\ldots,g_{m}(\theta_{m})\right) g ( θ ) = ( g 1 ( θ 1 ) , … , g m ( θ m ) )
∂ g ( θ ) ∂ θ = d i a g ( g 1 ′ ( θ 1 ) , … , g m ′ ( θ m ) ) = d i a g ( g ′ ( θ ) ) \frac{\partial\mathrm{\mathbf{g}}(\boldsymbol{\theta})}{\partial\boldsymbol{\theta}}=\mathrm{diag}\left(g'_{1}(\theta_{1}),\ldots,g'_{m}(\theta_{m})\right)=\mathrm{diag}\left(\mathbf{g}'\left(\boldsymbol{\theta}\right)\right) ∂ θ ∂ g ( θ ) = d i a g ( g 1 ′ ( θ 1 ) , … , g m ′ ( θ m ) ) = d i a g ( g ′ ( θ ) )
Back-Propagation
כדי להשתמש בשיטות גרדיאנט נרצה לחשב נגזרות לפי פרמטרי הרשת. באופן כללי אנו צריכים לחשב את הנגזרות של פונקציית ההפסד ביחס לכל פרמטרי הרשת (משקולות ואיברי הטיה), כלומר
∂ L ( W ) ∂ W ℓ \frac{\mathcal{\partial L}(W)}{\partial W_{\ell}} ∂ W ℓ ∂ L ( W ) כאשר W ℓ W_{\ell} W ℓ ℓ \ell ℓ
∂ L ( W ) ∂ W ℓ = ∂ L ( W ) ∂ z ℓ ∂ z ℓ ∂ W ℓ = ∂ L ( W ) ∂ z ℓ ∂ z ℓ ∂ u ℓ ∂ u ℓ ∂ W ℓ ∂ u ℓ ∂ W ℓ = z ℓ − 1 ∂ z ℓ ∂ u ℓ = d i a g ( φ ℓ ′ ( u ℓ ) ) \begin{aligned}
\frac{\mathcal{\partial L}(W)}{\partial W_{\ell}} &= \frac{\mathcal{\partial L}(W)}{\partial z_{\ell}}\frac{\partial z_{\ell}}{\partial W_{\ell}}=\frac{\mathcal{\partial L}(W)}{\partial z_{\ell}}\frac{\partial z_{\ell}}{\partial u_{\ell}}\frac{\partial u_{\ell}}{\partial W_{\ell}} \\
\frac{\partial\mathbf{u}_{\ell}}{\partial W_{\ell}} & =\mathbf{z}_{\ell-1} \\
\frac{\partial\mathbf{z}_{\ell}}{\partial\mathbf{u}_{\ell}} & =\mathrm{diag}\left(\varphi'_{\ell}\left(\mathbf{u}_{\ell}\right)\right)
\end{aligned} ∂ W ℓ ∂ L ( W ) ∂ W ℓ ∂ u ℓ ∂ u ℓ ∂ z ℓ = ∂ z ℓ ∂ L ( W ) ∂ W ℓ ∂ z ℓ = ∂ z ℓ ∂ L ( W ) ∂ u ℓ ∂ z ℓ ∂ W ℓ ∂ u ℓ = z ℓ − 1 = d i a g ( φ ℓ ′ ( u ℓ ) ) כאשר הנגזרת המאתגרת היחידה לחישוב היא הראשונה.
Back-Propagation
שיטה המקלה על חישוב הנגזרות על ידי שימוש בכלל השרשרת.
כלל השרשרת - תזכורת
במקרה הסקלרי:
( f ( g ( x ) ) ) ′ = f ′ ( g ( x ) ) ⋅ g ′ ( x ) \left(f(g(x))\right)'=f'(g(x))\cdot g'(x) ( f ( g ( x ) ) ) ′ = f ′ ( g ( x ) ) ⋅ g ′ ( x ) במקרה של מספר משתנים:
d d x f ( z 1 ( x ) , z 2 ( x ) , z 3 ( x ) ) = ( ∂ ∂ z 1 f ( z 1 ( x ) , z 2 ( x ) , z 3 ( x ) ) ) d d x z 1 ( x ) + ( ∂ ∂ z 2 f ( z 1 ( x ) , z 2 ( x ) , z 3 ( x ) ) ) d d x z 2 ( x ) + ( ∂ ∂ z 3 f ( z 1 ( x ) , z 2 ( x ) , z 3 ( x ) ) ) d d x z 3 ( x ) \begin{aligned}
\frac{d}{dx} f(z_1(x),z_2(x),z_3(x))
=& &\left(\frac{\partial}{\partial z_1} f(z_1(x),z_2(x),z_3(x))\right)\frac{d}{dx}z_1(x)\\
&+&\left(\frac{\partial}{\partial z_2} f(z_1(x),z_2(x),z_3(x))\right)\frac{d}{dx}z_2(x)\\
&+&\left(\frac{\partial}{\partial z_3} f(z_1(x),z_2(x),z_3(x))\right)\frac{d}{dx}z_3(x)\\
\end{aligned} d x d f ( z 1 ( x ) , z 2 ( x ) , z 3 ( x ) ) = + + ( ∂ z 1 ∂ f ( z 1 ( x ) , z 2 ( x ) , z 3 ( x ) ) ) d x d z 1 ( x ) ( ∂ z 2 ∂ f ( z 1 ( x ) , z 2 ( x ) , z 3 ( x ) ) ) d x d z 2 ( x ) ( ∂ z 3 ∂ f ( z 1 ( x ) , z 2 ( x ) , z 3 ( x ) ) ) d x d z 3 ( x )
Back-Propagation
לאלגוריתם 2 שלבים:
Forward pass : העברה של הדגימות דרך הרשת ושמירה של כל ערכי הביניים.Backward pass : חישוב של הנגזרות של הנוירונים מהמוצא של הרשת לכיוון הכניסה.
Back-Propagation :דוגמא פשוטה
נרצה לחשב את ∂ L / ∂ θ i \partial\mathcal{L}/\partial\theta_{i} ∂ L / ∂ θ i θ i \theta_{i} θ i L = ( y − t ) 2 , L=(y-t)^{2}, L = ( y − t ) 2 , t t t
∂ L ∂ θ i = 2 ( y − t ) ∂ y ∂ θ i \frac{\partial L}{\partial\theta_{i}}=2\left(y-t\right)\frac{\partial y}{\partial\theta_{i}} ∂ θ i ∂ L = 2 ( y − t ) ∂ θ i ∂ y ובאופן דומה עבור שאר פונקציות ההפסד. כך, עלינו להתמקד בנגזרת של המוצא ביחס לפרמטר.
Back-Propagation :דוגמא פשוטה
נרשום את הנגזרת של y y y θ 2 \theta_2 θ 2
∂ y ∂ θ 2 = ∂ y ∂ z 2 ∂ z 2 ∂ θ 2 = ∂ y ∂ z 2 ∂ ∂ θ 2 h 2 ( z 1 ; θ 2 ) \frac{\partial y}{\partial\theta_2}=\frac{\partial y}{\partial z_2}\frac{\partial z_2}{\partial \theta_2}=\frac{\partial y}{\partial z_2}\frac{\partial}{\partial \theta_2}h_2(z_1;\theta_2) ∂ θ 2 ∂ y = ∂ z 2 ∂ y ∂ θ 2 ∂ z 2 = ∂ z 2 ∂ y ∂ θ 2 ∂ h 2 ( z 1 ; θ 2 ) נוכל לפרק גם את הנגזרת של d y d z 2 \frac{dy}{dz_2} d z 2 d y
∂ y ∂ z 2 = ∂ y ∂ z 3 ∂ z 3 ∂ z 2 = ∂ ∂ z 3 h 4 ( z 3 ; θ 4 ) ∂ ∂ z 2 h 3 ( z 2 ; θ 3 ) \frac{\partial y}{\partial z_2}=\frac{\partial y}{\partial z_3}\frac{\partial z_3}{\partial z_2}=\frac{\partial}{\partial z_3}h_4(z_3;\theta_4)\frac{\partial}{\partial z_2}h_3(z_2;\theta_3) ∂ z 2 ∂ y = ∂ z 3 ∂ y ∂ z 2 ∂ z 3 = ∂ z 3 ∂ h 4 ( z 3 ; θ 4 ) ∂ z 2 ∂ h 3 ( z 2 ; θ 3 ) לכן:
∂ y ∂ θ 2 = ∂ y ∂ z 3 ∂ z 3 ∂ z 2 ∂ z 2 ∂ θ 2 = ∂ ∂ z 3 h 4 ( z 3 ; θ 4 ) ∂ ∂ z 2 h 3 ( z 2 ; θ 3 ) ∂ ∂ θ 2 h 2 ( z 1 ; θ 2 ) \frac{\partial y}{\partial\theta_2}=\frac{\partial y}{\partial z_3}\frac{\partial z_3}{\partial z_2}\frac{\partial z_2}{\partial\theta_2}=\frac{\partial}{\partial z_3}h_4(z_3;\theta_4)\frac{\partial}{\partial z_2}h_3(z_2;\theta_3)\frac{\partial}{\partial \theta_2}h_2(z_1;\theta_2) ∂ θ 2 ∂ y = ∂ z 3 ∂ y ∂ z 2 ∂ z 3 ∂ θ 2 ∂ z 2 = ∂ z 3 ∂ h 4 ( z 3 ; θ 4 ) ∂ z 2 ∂ h 3 ( z 2 ; θ 3 ) ∂ θ 2 ∂ h 2 ( z 1 ; θ 2 )
Back-Propagation :דוגמא פשוטה
∂ y ∂ θ 2 = ∂ y ∂ z 3 ∂ z 3 ∂ z 2 ∂ z 2 ∂ θ 2 = ∂ ∂ z 3 h 4 ( z 3 ; θ 4 ) ∂ ∂ z 2 h 3 ( z 2 ; θ 3 ) ∂ ∂ θ 2 h 2 ( z 1 ; θ 2 ) \frac{\partial y}{\partial\theta_2}=\frac{\partial y}{\partial z_3}\frac{\partial z_3}{\partial z_2}\frac{\partial z_2}{\partial\theta_2}=\frac{\partial}{\partial z_3}h_4(z_3;\theta_4)\frac{\partial}{\partial z_2}h_3(z_2;\theta_3)\frac{\partial}{\partial\theta_2}h_2(z_1;\theta_2) ∂ θ 2 ∂ y = ∂ z 3 ∂ y ∂ z 2 ∂ z 3 ∂ θ 2 ∂ z 2 = ∂ z 3 ∂ h 4 ( z 3 ; θ 4 ) ∂ z 2 ∂ h 3 ( z 2 ; θ 3 ) ∂ θ 2 ∂ h 2 ( z 1 ; θ 2 ) כדי לחשב את הביטוי שקיבלנו עלינו לבצע את שני השלבים הבאים:
לחשב את כל ה z i z_i z i
לחשב את כל הנגזרות מהמוצא של הרשת ועד לנקודה בה נמצא הפרמטר שלפיו רוצים לגזור (backward-pass).
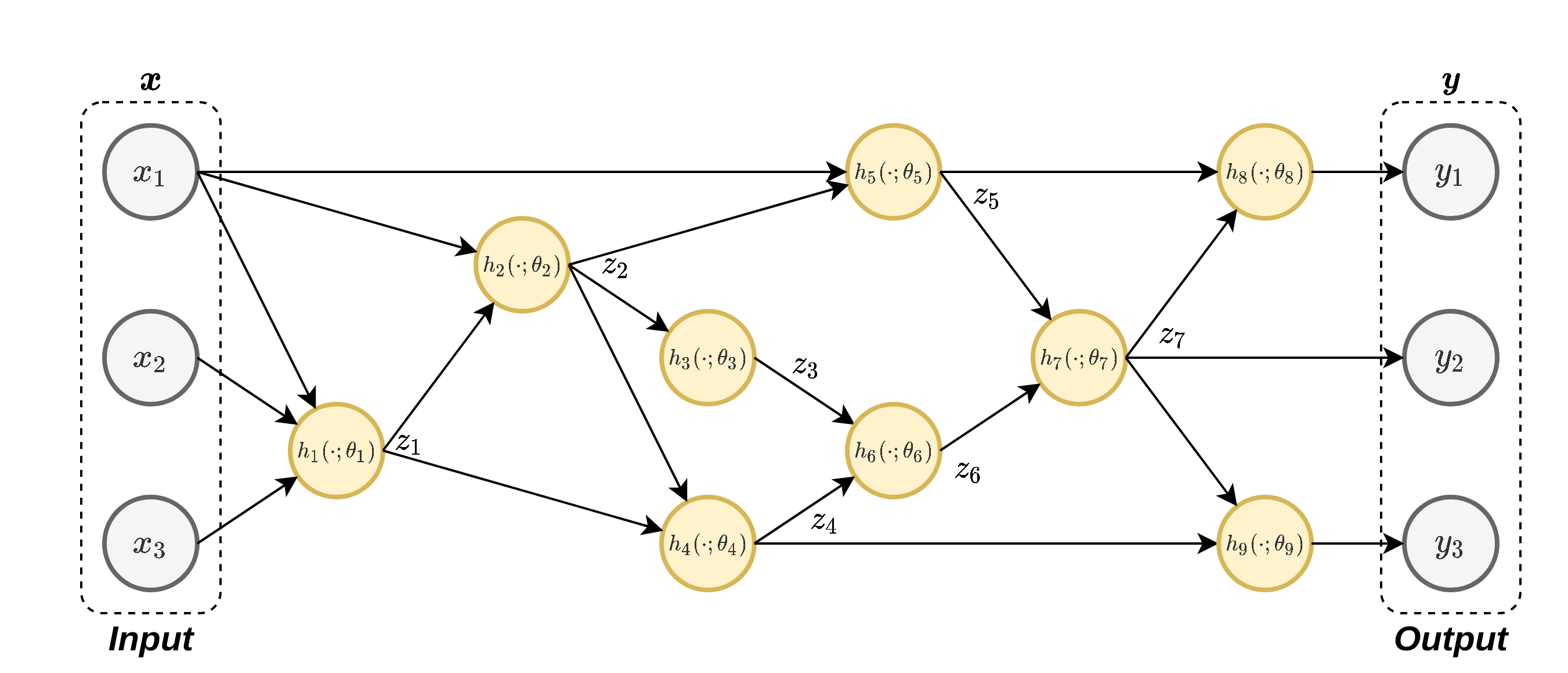
Back-Propagation :דוגמא מעט יותר מורכבת
נחשב את הנגזרת של y 1 y_1 y 1 θ 3 \theta_3 θ 3
Back-Propagation :דוגמא מעט יותר מורכבת
נפרק את הנגזרת של ∂ y 1 ∂ θ 3 \frac{\partial y_1}{\partial\theta_3} ∂ θ 3 ∂ y 1
∂ y 1 ∂ θ 3 = ∂ y 1 ∂ z 7 ∂ z 7 ∂ z 6 ∂ z 6 ∂ z 3 ∂ z 3 ∂ θ 3 = ∂ ∂ z 7 h 8 ( z 7 ; θ 8 ) ∂ ∂ z 6 h 7 ( z 6 ; θ 7 ) ∂ ∂ z 3 h 6 ( z 5 ; θ 6 ) ∂ ∂ θ 3 h 3 ( z 2 ; θ 3 ) \begin{aligned}
\frac{\partial y_1}{\partial\theta_3}
&=\frac{\partial y_1}{\partial z_7}\frac{\partial z_7}{\partial z_6}\frac{\partial z_6}{\partial z_3}\frac{\partial z_3}{\partial\theta_3}\\
&=\frac{\partial}{\partial z_7}h_8(z_7;\theta_8)\frac{\partial}{\partial z_6}h_7(z_6;\theta_7)\frac{\partial}{\partial z_3}h_6(z_5;\theta_6)\frac{\partial}{\partial\theta_3}h_3(z_2;\theta_3)
\end{aligned} ∂ θ 3 ∂ y 1 = ∂ z 7 ∂ y 1 ∂ z 6 ∂ z 7 ∂ z 3 ∂ z 6 ∂ θ 3 ∂ z 3 = ∂ z 7 ∂ h 8 ( z 7 ; θ 8 ) ∂ z 6 ∂ h 7 ( z 6 ; θ 7 ) ∂ z 3 ∂ h 6 ( z 5 ; θ 6 ) ∂ θ 3 ∂ h 3 ( z 2 ; θ 3 )
Back-Propagation :דוגמא מעט יותר מורכבת
∂ y 1 ∂ θ 3 = ∂ y 1 ∂ z 7 ∂ z 7 ∂ z 6 ∂ z 6 ∂ z 3 ∂ z 3 ∂ θ 3 = ∂ ∂ z 7 h 8 ( z 7 ; θ 8 ) ∂ ∂ z 6 h 7 ( z 6 ; θ 7 ) ∂ ∂ z 3 h 6 ( z 5 ; θ 6 ) ∂ ∂ θ 3 h 3 ( z 2 ; θ 3 ) \begin{aligned}
\frac{\partial y_1}{\partial\theta_3}
&=\frac{\partial y_1}{\partial z_7}\frac{\partial z_7}{\partial z_6}\frac{\partial z_6}{\partial z_3}\frac{\partial z_3}{\partial\theta_3}\\
&=\frac{\partial}{\partial z_7}h_8(z_7;\theta_8)\frac{\partial}{\partial z_6}h_7(z_6;\theta_7)\frac{\partial}{\partial z_3}h_6(z_5;\theta_6)\frac{\partial}{\partial\theta_3}h_3(z_2;\theta_3)
\end{aligned} ∂ θ 3 ∂ y 1 = ∂ z 7 ∂ y 1 ∂ z 6 ∂ z 7 ∂ z 3 ∂ z 6 ∂ θ 3 ∂ z 3 = ∂ z 7 ∂ h 8 ( z 7 ; θ 8 ) ∂ z 6 ∂ h 7 ( z 6 ; θ 7 ) ∂ z 3 ∂ h 6 ( z 5 ; θ 6 ) ∂ θ 3 ∂ h 3 ( z 2 ; θ 3 )
נריץ את ה forward-pass בשביל לחשב את ערכי ה z i z_i z i
נריץ את ה backward-pass בו נחשב את הנגזרות מהמוצא של הרשת עד לנגזרת של h 3 h_3 h 3
Back-Propagation - MLP
משוואות ה forward-pass:
z 1 = φ ( W 1 x + b 1 ⏟ u 1 ) , W 1 ∼ d 1 × d i n z 2 = φ ( W 2 z 1 + b 2 ⏟ u 2 ) , W 2 ∼ d 2 × d 1 y = w 3 T z 2 + b 3 , w 3 ∼ d 2 × 1 \boldsymbol{z}_1=\varphi(\underbrace{W_1\boldsymbol{x}+\boldsymbol{b}_1}_{\boldsymbol{u}_1}), \qquad W_1 \sim d_1 \times d_{in} \\
\boldsymbol{z}_2=\varphi(\underbrace{W_2\boldsymbol{z}_1+\boldsymbol{b}_2}_{\boldsymbol{u}_2}), \qquad W_2 \sim d_2 \times d_1 \\
y=\boldsymbol{w}_3^T\boldsymbol{z}_2+\boldsymbol{b}_3, \qquad w_3 \sim d_2 \times 1 \\ z 1 = φ ( u 1 W 1 x + b 1 ) , W 1 ∼ d 1 × d i n z 2 = φ ( u 2 W 2 z 1 + b 2 ) , W 2 ∼ d 2 × d 1 y = w 3 T z 2 + b 3 , w 3 ∼ d 2 × 1
Back-Propagation and MLPs
Forward pass
z 0 = x u ℓ = W ℓ z l − 1 + b ℓ for l = 1 to L z ℓ = φ ℓ ( u ℓ ) for l = 1 to L \begin{aligned}\mathbf{z}_{0} & =\mathbf{x}\\
\mathbf{u}_{\ell} & =W_{\ell}\mathbf{z}_{l-1}+\mathbf{b}_{\ell}\quad\text{for }l=1\text{ to }L\\
\mathbf{z}_{\ell} & =\varphi_{\ell}(\mathbf{u}_{\ell})\quad\text{for }l=1\text{ to }L
\end{aligned} z 0 u ℓ z ℓ = x = W ℓ z l − 1 + b ℓ for l = 1 to L = φ ℓ ( u ℓ ) for l = 1 to L Backward pass
δ L = d i a g ( φ L ′ ( u L ) ) ∂ L ∂ z L δ ℓ = d i a g ( φ ℓ ′ ( u ℓ ) ) W ℓ + 1 ⊤ δ ℓ + 1 for l = L − 1 to 1 \begin{aligned}
\delta_{L} &=\mathrm{diag}\left(\varphi'_{L}(u_{L})\right) \frac{\mathcal{\partial L}}{\partial z_{L}} \\
\delta_{\ell} &= \mathrm{diag}\left(\varphi'_{\ell}(u_{\ell})\right) W_{\ell+1}^{\top}\delta_{\ell+1}\quad\text{for }l=L-1\text{ to }1
\end{aligned} δ L δ ℓ = d i a g ( φ L ′ ( u L ) ) ∂ z L ∂ L = d i a g ( φ ℓ ′ ( u ℓ ) ) W ℓ + 1 ⊤ δ ℓ + 1 for l = L − 1 to 1
Back-Propagation and MLPs
חישוב הגרדיאנט יתבצע באמצעות
∇ W ℓ L = δ ℓ z ℓ − 1 ⊤ ; ∇ b ℓ L = δ ℓ \nabla_{W_{\ell}}\mathcal{L}=\delta_{\ell}z_{\ell-1}^{\top}\quad;\quad\nabla_{b_{\ell}}\mathcal{L}=\delta_{\ell} ∇ W ℓ L = δ ℓ z ℓ − 1 ⊤ ; ∇ b ℓ L = δ ℓ ואלגוריתם הגדריאנט יהיה
W ℓ ( t + 1 ) = W ℓ ( t ) − η δ ℓ ( t ) z ℓ − 1 ( t ) ⊤ ; b ℓ ( t + 1 ) = b ℓ ( t ) − η δ ℓ ( t ) W_{\ell}^{(t+1)}=W_{\ell}^{(t)}-\eta\delta_{\ell}^{(t)}z_{\ell-1}^{(t)\top}\quad;\quad b_{\ell}^{(t+1)}=b_{\ell}^{(t)}-\eta\delta_{\ell}^{(t)} W ℓ ( t + 1 ) = W ℓ ( t ) − η δ ℓ ( t ) z ℓ − 1 ( t ) ⊤ ; b ℓ ( t + 1 ) = b ℓ ( t ) − η δ ℓ ( t )