תרגול 3 - Generalization & overfitting
תקציר התיאוריה
מושגים
- הכללה (generalization): היכולת להסיק מן הפרט אל הכלל. היכולת של המודל להפיק תוצאות טובות גם על דגימות אשר לא הופיעו במדגם.
- Overfitting (התאמת יתר): התופעה שבה המודל לומד מאפיינים אשר מופיעים רק במדגם והם אינם מייצגים את התכונות של הפילוג האמיתי. Overfitting פוגע ביכולת ההכללה.
- הערכת הביצועים / הציון של חזאי (יכולת הכללה): הערכת המחיר (המתקבל מפונקציית המחיר) המתקבל בעבור חזאי נתון על הפילוג האמיתי.
- יכולת הביטוי (expressiveness) של מודל פרמטרי: היכולת של מודל פרמטרי לייצג (או לקרב) מגוון רחב של מודלים. לדוגמא לפולינום מסדר מאד גבוה יהיה יכולת ביטוי גבוהה בעוד שלמודל לינארי תהיה יכולת ביטוי נמוכה.
-
Hyper parameters - הפרמטרים אשר משפיעים על המודל הפרמטרי או האלגוריתם, אך אינם חלק מהפרמטרים שעליהם אנו מבצעים את האופטימיזציה. דוגמאות:
- סדר הפולינום שבו אנו משתמשים
- הפרמטר אשר קובע את גודל הצעד באלגוריתם ה gradient descent.
- פרמטרים אשר קובעים את המבנה של רשת נוירונים.
- סדר המודל: כאשר ישנו hyper-parameter אשר שולט ביכולת הביטוי של המודל הפרמטרי (כגון המקרה של סדר של פולינום) אנו נכנה פרמטר זה לרוב הסדר של המודל.
הערכת ביצועים בעזרת test set (סט בחן)
במקרים בהם פונקציית המחיר מוגדרת בעזרת תוחלת (כמו במקרה הנפוץ של שימוש בפונקציות סיכון / הפסד) ניתן לשערך את ביצועיו של חזאי מסויים על ידי שימוש בתוחלת אמפירית ומדגם נוסף . לשם כך נפצל את המודל לשני תתי מדגמים:
- Train set (סט אימון): בו נשתמש לבנות את החזאי.
- Test set (סט בחן): בו נשתמש בכדי להעריך את ביצועי המערכת.
גדולו של ה test set
מצד אחד נרצה שסט הבחן יהיה גדול מספיק על מנת שיקרב בצורה טובה את ביצועיו האמיתיים של המודל אך מצד שני לא נרצה לגרוע יותר מידי דגימות מה training set. במקרים בהם המדגם מספיק גדול לא תהיה בעיה להפריש test set מספיק גדול מבלי לפגוע משמעותית בגודל המדגם, במקרים אחרים מקובל להשתמש בפיצול של 80% train ו20% test.
פירוק שגיאת החיזוי
בקורס זה נציג שני פירוקים נפוצים של שגיאת החיזוי בבעיות supervised learning.
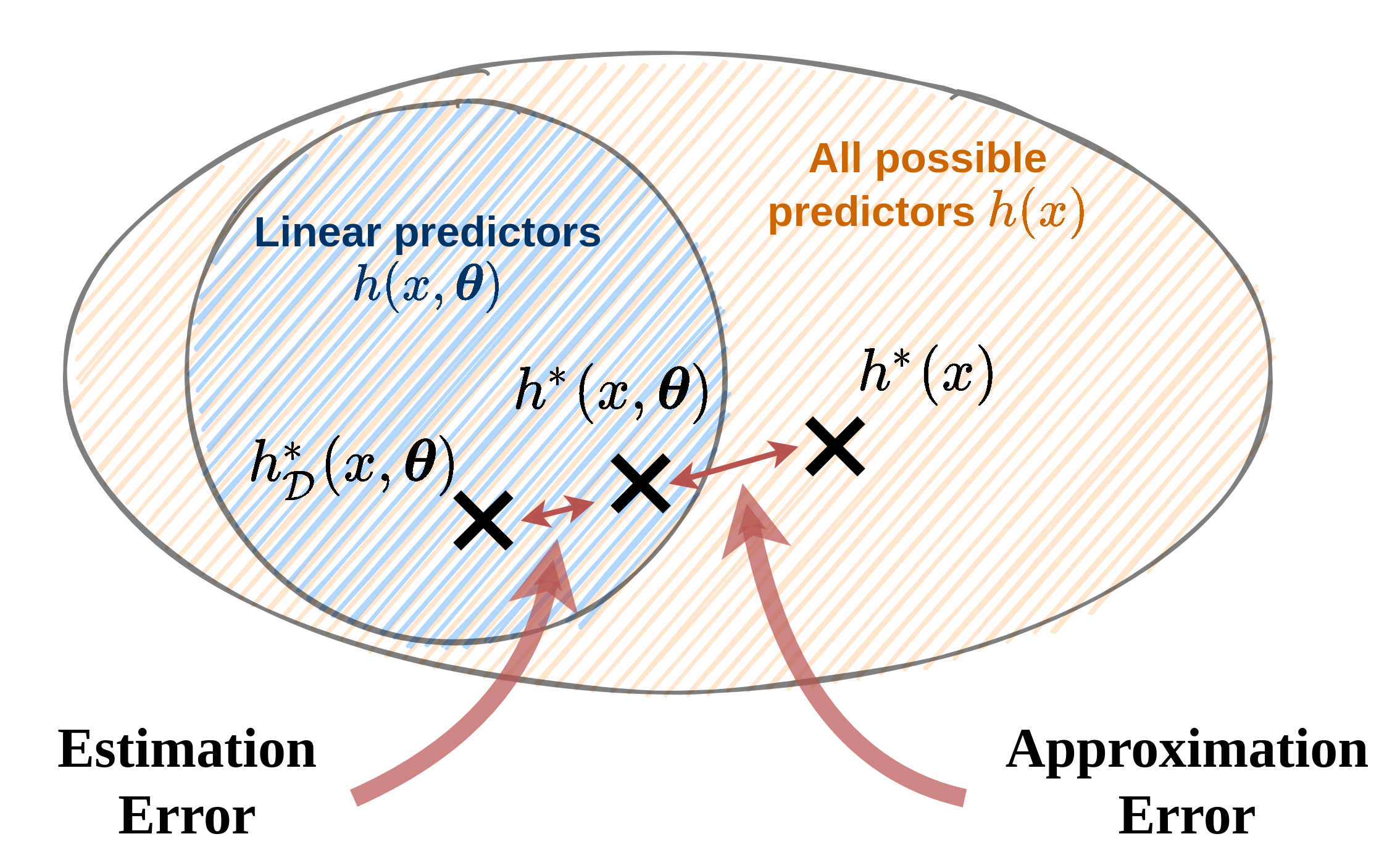
Aprroximation-estimation decomposition
פירוק זה הוא רק רעיוני ולרוב לא ניתן לחשב אותו בפועל. בפירוק זה נתייחס לשלושת הגורמים הבאים בשגיאת החיזוי:
- Noise - ה"רעש" של התויות: השגיאה שהחזאי האופטימאלי צפוי לעשות. שגיאה זו נובעת מהאקראיות של התויות .
- Approximation error - שגיאת קירוב: השגיאה עקב ההגבלה של המודל למשפחה מצומצמת של מודלים (לרוב למודל פרמטרי). שגיאה זו נובעת מההבדל בין המודל האופטימאלי לבין המודל הפרמטרי האופטימאלי .
- Estimation error - שגיאת השיערוך: השגיאה הנובעת מהשימוש במדגם כתחליף לפילוג האמיתי וחוסר היכולת שלנו למצוא את המודל הפרמטרי האופטימאלי. שגיאה זו נובעת מההבדל בין המודל הפרמטרי האופטימאלי למודל הפרמטרי המשוערך על סמך המדגם .
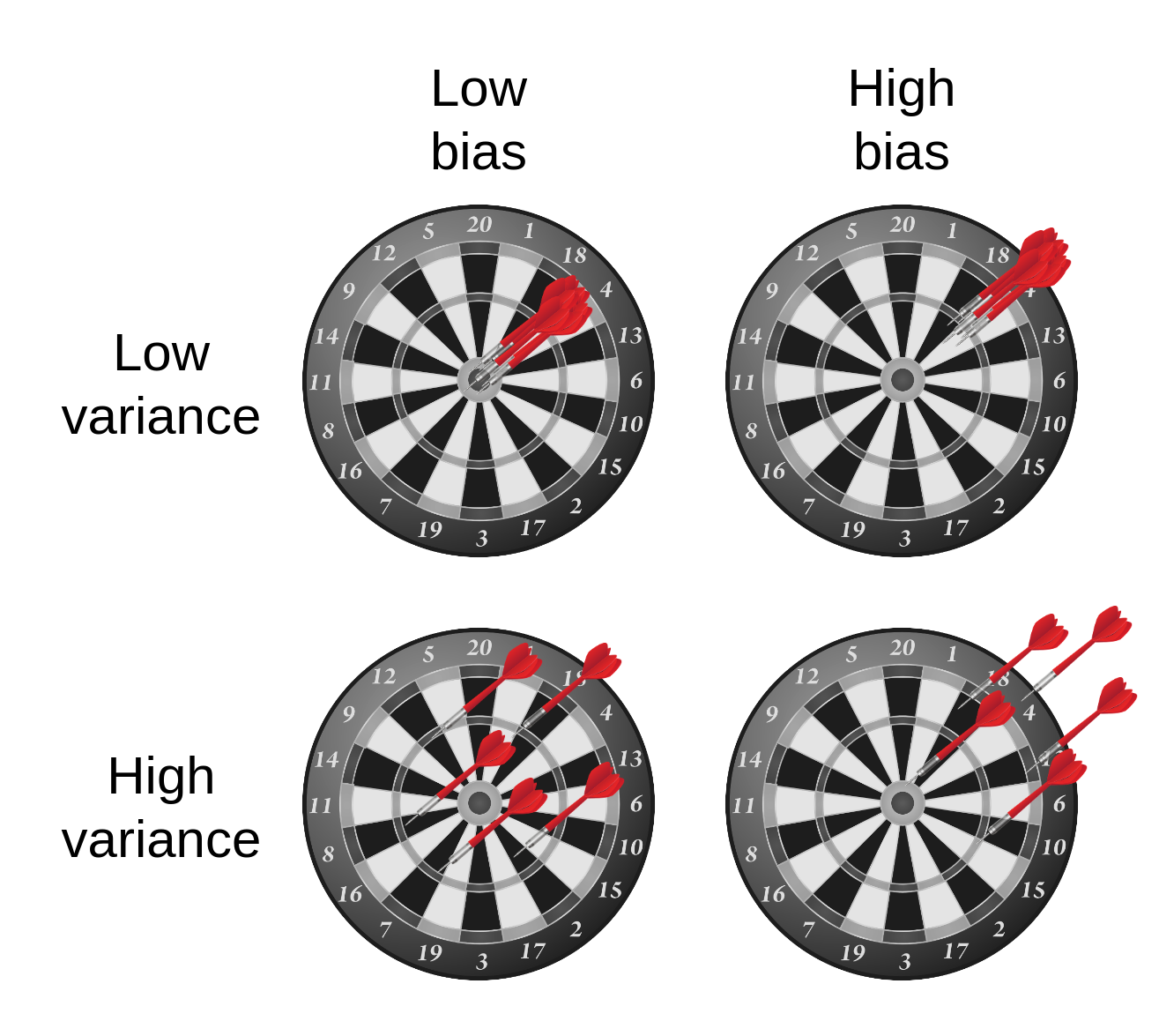
Bias-variance decomposition
פירוק זה מתייחס למקרים שבהם פונקציית המחיר הינה MSE (או RMSE).
המדגם שאיתו אנו עובדים הוא אקראי (משום שהוא אוסף של דגימות אקראיות) ולכן גם החזאי שאותו נייצר על סמך המדגם הוא אקראי. נגדיר את החזאי הממוצע כחזאי המתקבל כאשר לוקחים תוחלת על החזאים המיוצרים על ידי אלגוריתם מסויים על פני כל המדגמים האפשריים.
לשם הבהירות, אנו נשתמש בסימון בכדי לציין תוחלת על פני המדגמים האפשריים. (תוחלת ללא סימון תהיה לפי ו ).
בעבור המקרה של MSE אנו יודעים כי החזאי האופטימאלי הינו: . על ידי שימוש בחזאי האופטימאלי והחזאי הממוצע ניתן לפרק את התוחלת על שגיאת ה MSE של אלגוריתם נתון באופן הבא:
בפירוק הזה:
- ה variance מודד את השונות של החזאים השונים המתקבלים ממדגמים שונים סביב החזאי הממוצע. זהו האיבר היחיד בפירוק אשר תלוי בפילוג של המדגם.
- ה bias מודד את ההפרש הריבועי בין החיזוי של החזאי הממוצע לבין החיזוי של החזאי האופטימאלי.
- ה noise (בודמה לפירוק הקודם) מודד את השגיאה הריבועית המתקבלת בעבור החיזוי האופטימאלי (אשר נובעת מהאקראיות של ).
בתרגיל 3.1 נפתח את הפירוק הזה.
אילוסטרציה של bias ו variance:
Tradeoffs
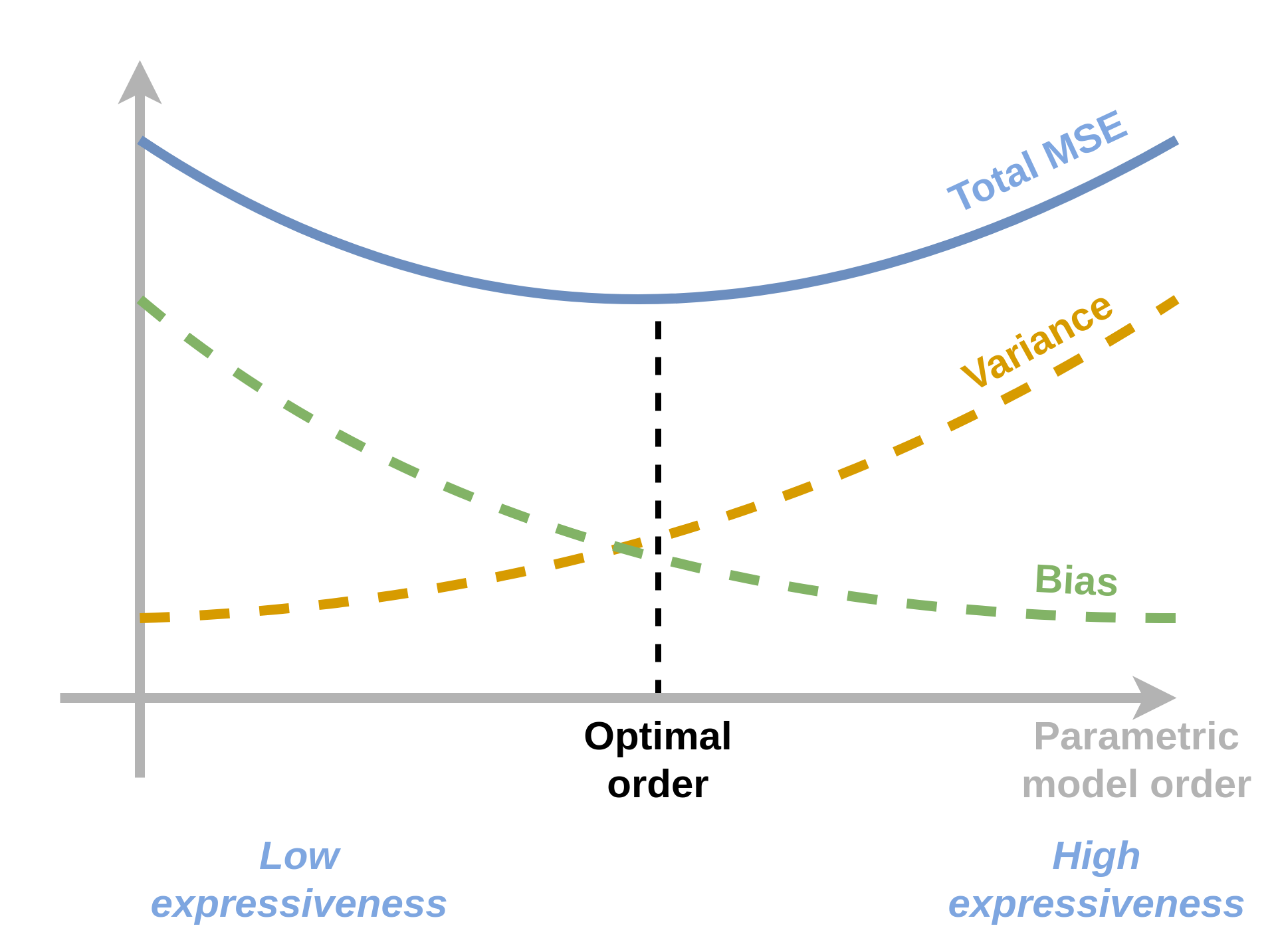
יכולת הביטוי של המודל הפרמטרי לרוב ישפיע מאד על גודלם של השגיאות אותם נקבל. לרוב התלות של השגיאות המתקבלות ביכולת הביטוי של המודל תקיים את הקשר הבא:
- מודל בעל יכולת ביטוי גבוהה לרוב יהיה בעל שגיאת קירוב / bias נמוך אך שגיאת שיערוך / variance גבוה.
- מודל בעל יכולת ביטוי נמוכה לרוב יהיה בעל שגיאת שיערוך / variance נמוך אך שגיאת קירוב / bias גבוה.
המודל עם הביצועים הטובים ביותר (יכולת הכללה טובה) ימצא באיזו שהיא נקודת ביניים בין שני הקצוות הנל, כפי שמתואר בשירטוט הסכימתי הבא:
שימוש ב validataion set לקביעת hyper-parameters
מכיוון שה hyper-parameters אינם חלק מבעיית האופטימיזציה אנו צריכים דרך אחרת לקבוע אותם. לרוב נאלץ לקבוע את הפרמטרים האלו בשיטה של ניסוי וטעיה. זאת אומרת שיהיה עלינו פשוט נסות ערכים שונים ולבדוק את ביצועי המודל בעבור אותם ערכים.
מכיוון שאנו לא יכולים להשתמש ב test set בכדי לבנות את המודל שלנו אנו צריכים ליייצר מדגם ניפרד נוסף שעליו נוכל לבחון את ביצועי המודל בעבור ערכים שונים של ה hyper-parameters. אנו נייצר מדגם זה על ידי חלוקה נוספת של ה train set. למדגם הנוסף נקרא validation set.
במקרים רבים לאחר קביעת ה hyper-parmaeters אנו נאחד חזרה את ה validation set וה train set ונאמן מחדש את המודל על המדגם המאוחד (כל הדגימות מלבד ה test set).
רגולריזציה
דרך נוספת לנסות ולהקטין את ה overfitting של המודל על ידי הוספת איבר רגולריזציה לבעיית האופטימיזציה. מטרת איבר הרגולריזציה הינה להשתמש בידע מוקדם שיש לנו על אופי הבעיה לצורך בחירת המודל. הדרך שבה איבר הרגולריזציה עושה זאת הינה על ידי הוספת תיקון לבעיית האופטימיזציה כך שמודלים שלדעתינו פחות סבירים יקבלו ציון גבוהה יותר. לרוב אנו נוסיף לבעיית האופטימיזציה את איבר הרגולריציה יחד עם קבוע כפלי נוסף אשר קובע את המשקל שאנו מעוניינים לתת לרגולריזציה.
בעיות אופטימיזציה עם רגולריזציה יהיו מהצורה הבא:
שתי הרגולריזציות הנפוצות ביותר הינן:
- - אשר מוסיפה איבר רגולריזציה של .
- - (Tikhonov regularizaion) אשר מוסיפה איבר רגולריזציה של .
רגולריזציות אלו מנסות לשמור את הפרמטריים כמה שיותר קטנים. המוטיבציה מאחורי הרצון לשמור את הפרמטרים קטנים הינה העובדה שבמרבית המודלים ככל שהפרמטרים קטנים יותר המודל הנלמד יהיה בעל נגזרות קטנות יותר ולכן הוא ישתנה לאט יותר ופחות "ישתולל".
המשקל אותו אנו נותנים לרגולריזציה הוא hyper-parameter של האלגוריתם שאותו יש לקבוע בעזרת ה validation set.
דוגמא: בעיות LLS עם רגולריזציה
Ridge regression: LLS + regularization
גם לבעיה זו יש פתרון סגור והוא נתון על ידי:
אנו נראה את הפתוח של פתרון זה בתרגיל 3.2.
LASSO: LLS + regularization
(LASSO = Linear Absolute Shrinkage and Selection Opperator)
לבעיה זו אין פתרון סגור ויש צורך להשתמש באלגוריתמים איטרטיביים כגון gradient descent.
תרגיל 3.1 - Bias-variance decomposition
1) הראו כי בעבור משתנה אקראי כל שהוא וקבוע ניתן לפרק את התחולת של המרחק הריבועי בין לבין באופן הבא:
2) הראו כי בעבור אלגוריתם אשר מייצר חזאיים בהינתן מדגמים , ניתן לפרק את התוחלת (על פני מדגמים וחיזויים שונים) של שגיאת ה MSE באופן הבא:
כאשר:
ו
הדרכה:
-
הראו ראשית כי ניתן לפרק את שגיאת ה MSE בעבור מדגם נתון באופן הבא:
לשם כך השתמשו בהחלקה על מנת להתנות את התוחלת ב ולקבל תוחלת לפי . הפעילו את הזהות מסעיף 1 על התוחלת של .
-
הראו כי ניתן לפרק את התוחלת הזו באופן הבא:
לשם כך החליפו את סדר התוחלות והשתמשו בזהות מסעיף 1 על התוחלת לפי .
- השתמשו בשני הפירוקים הנ"ל על עמת להראות את פירוק ה bias-variance המלא.
3) הניחו כי כאשר גודל המדגם הולך וגדל החזאים המתקבלים מהמודל מתכנסים (במובן הסתברותי) לחזאי ה"ממוצע": . מה תוכלו לומר על התלות של איברי השגיאה בגודל המדגם?
(ניתן להניח שכפי שקורה במרבית האלגוריתמים ש אינו תלוי בגודל המגדם)
4) על פי תוצאת הסעיף הקודם, כיצד לדעתכם עשוי להשפיע גודל המדגם על סדר המודל שאותו נרצה לבחור?
פתרון 3.1
1)
הזהות שאותה נתבקשנו להוכיח היא למעשה הכללה של הקשר הבא למשתנים אקראיים:
נוכיח את הזהות על ידי הוספה והחסרה של בתוך הסוגריים:
2)
שלב ראשון
נפעל על פי ההדרכה. נחליק על ידי התניה ב ונפעיל את הזהות מסעיף 1 על התוחלת הפנימית (לפי ):
נארגן מחדש את התוחלות:
נשתמש כעת בעובדה ש ונקבל:
בביטוי שקיבלנו האיבר הראשון הוא למעשה השגיאה הנובעת מההבדל בין החיזוי של מודל האידאלי לבין החיזוי של מודל ספציפי ששנוצר ממדגם מסויים. נשים לב שהאיבר הראשון לא תלוי בכלל בפילוג של . האיבר השני בביטוי שקיבלנו הוא השגיאה אותה עושה החזאי האופטימאלי והיא נובע מחוסר היכולת לחזות את במדוייק. נשים לב כי האיבר השני לא תלוי כלל במדגם.
שלב שני
על פי ההדרכה נפרק את התוחלת הבאה על ידי החלפת סדר התוחלות ושימוש בזיהות מסעיף 1 על התוחלת לפי :
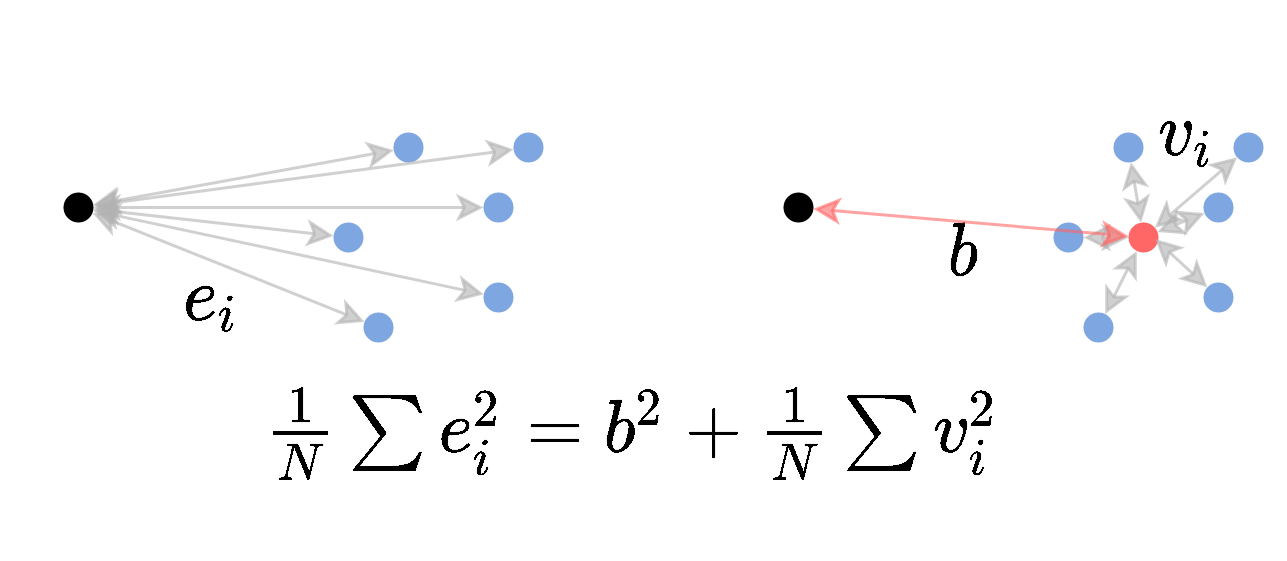
נשתמש בסימון ונקבל:
זהו הפירוק של השגיאה לרכיב ה variance של החזאי אשר מבטא את השגיאה הצפויה עקב ההשתנות של החזאי כתלות במדגם שאיתו נעבוד, ורכיב bias אשר מבטא את השגיאה אשר נובעת מההבדל בין החזאי ה"ממוצע" והחזאי האידאלי.
נרכיב את הכל
נשתמש בפירוק הראשון על מנת לקבל:
מכיוון שהאיבר השני לא תלוי ב נוכל להוציא אותו מהתוחלת על :
נציב את הפירוק מהשלב השני ונקבל:
3)
המשמעות של העובדה ש מתכנס לממוצע שלו במובן הסתברותי הינה למעשה שה variance שלו קטן. זאת אומרת שרכיב ה variance בפירוק הנ"ל יקטן. שאר האיברים במקרה זה לא יושפעו מהשינוי בגודלו של המדגם.
(ישנם מקרים פחות נפוצים שבהם גם החזאי הממוצע תלוי בגודל המדגם ואז גם הוא יכול להשתנות).
4)
השינוי של רכיב ה variance יכול כמובן להשפיע על סדר המודל האופטימאלי. באלגוריתמיים טיפוסיים שגיאת ה variance תהיה זו שמושכת את משפחת המודלים להיות כמה שיותר מצומצמת (בעוד ששגיאת ה bias כן מושכת בכיוון ההפוך). אנו נצפה שכאשר ה variance יקטן תקטן גם ההשפעה שלו על השגיאה הכוללת ולרוב ניתן יהיה להוסיף ולהקטין את השגיאה על ידי הגדלת הסדר של המודל הפרמטרי.
ננסה להמחיש זאת גם בעזרת הגרף הסכימתי הבא:
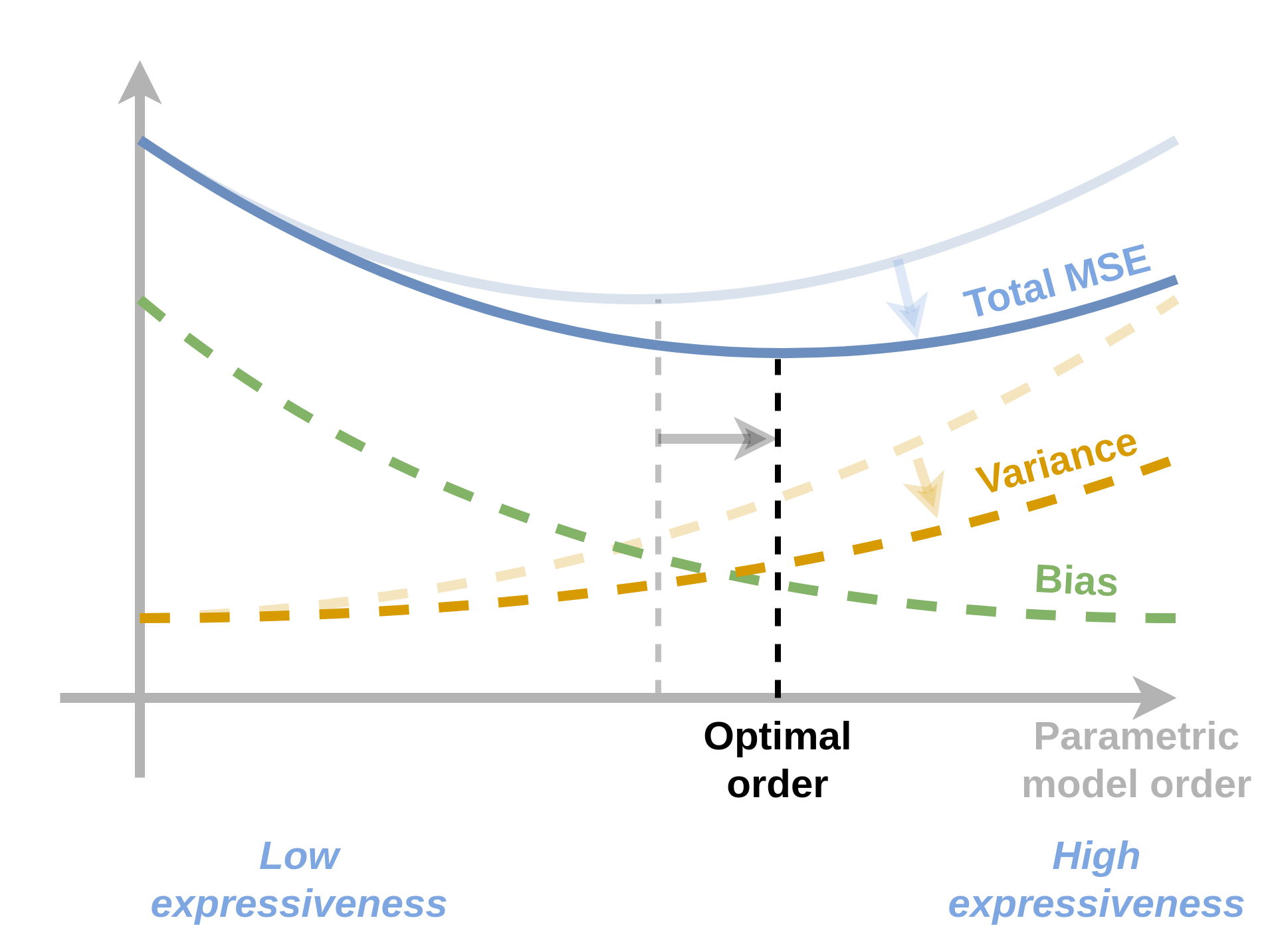
כאשר הגרף של שגיאת ה variance ירד אנו מצפים כי נקודת המינימום של השגיאה הכוללת תזוז ימינה לכיוון מודלים מסדר גבוהה יותר.
הערה: ניתוח זה כמובן נשען על התנהגות טיפוסית של אלגוריתמי supervised learning ואין הכרח שההתנהגות המתוארת בתשובה זו אכן תהיה ההתנהגות במציאות.
תרגיל 3.2 - רגולריזציה
1) בעבור Rigde regression (המקרה של LLS + regularization) רשמו את בעיית האופטימיזציה ופתרו אותה על ידי גזירה והשוואה ל-0.
2) נסתכל כעת על וריאציה של Ridge regression שבה אנו נותנים משקל שונה לרגולריזציה של כל פרמטר. זאת אומרת, אנו נרצה להשתמש באיבר רגולריזציה מהצורה:
(כאן הוא מספר הפרמטרים של המודל).
הדרכה: הגדירו את מטריצת המשקלים , רשמו את הבעיה בכתיב מטריצי ופתרו אותה בדומה לסעיף הקודם.
3) נסתכל כעת על אלגוריתם כללי שבו הפרמטרים של המודל נקבעים על פי בעיית האופטימיזציה הבאה
רשמו את הבעיות האופטימיזציה המתקבלות לאחר הוספה של איבר רגולריזציה מסוג ו .
4) רשמו את כלל העדכון של אלגוריתם הגרדיאנט בעבור כל אחת משתי הרגולריזציות.
5) על סמך ההבדל בין שני כללי העדכון הסבירו מה ההבדל בין האופן שבו שתי הרגולריזציות מנסות להקטין את הפרמטרים.
6) על סמך שני כללי העדכון הסבירו מדוע רגולריזציית נוטה יותר לאפס פרמטרים מאשר רגולריזציית . (הניחו שצעדי העדכון קטנים מאד)
פתרון 3.2
1)
תזכורת, בעיית ה LLS היא המקרה שבו אנו משתמשים ב
- MSE או RMSE כפונקציית המחיר / סיכון.
- ERM.
- מודל לינארי
בעיית האופטימיזציה של LLS הינה:
כאשר
כאשר נוסיף לבעיית האופטימיזציה איבר של רגולריזציית נקבל:
נזגור ונשווה ל-. נשתמש בנזגרת המוכרת :
ניתן כמובן "לבלוע" את ה בתוך הפרמטר , אך שינוי זה מצריך להתאים את הפרמטר לגודל המדגם ולעדכנו כאשר גודל המדגם משתנה (נגיד במקרה בו מפרישים חלק מהמדגם ל validation set).
2)
בעיית האופטימיזציה כעת תהיה
נפעל על פי ההדרכה. נגדיר את המטריצה:
בעזרת מטריצה זו ניתן לרשום את בעיית האופטימיזציה באופן הבא:
נגזור ונשווה ל-0:
3)
בעיית האופטימיזציה בתוספת רגולריזציית תהיה:
בעיית האופטימיזציה בתוספת רגולריזציית תהיה:
4)
כלל העדכון של gradient decsent הינו:
כאשר היא פונקציית המטרה של בעיית האפטימזציה. בעבור רגולריזציית ה נקבל:
בעבור רגולריזציית ה נקבל:
כאשר פונקציית ה פועלת איבר איבר.
5)
שני האיברים שנוספו לכלל העדכון מנסים בכל צעד להקטין את וקטור הפרמטריים ולקרב אותו ל-0. ההבדל בין שני האיברים הינו שבעוד שהאיבר המתקבל ברגולריזציית ה הינו פורפוציוני לגודל של האיברים בוקטור הפרמטרים האיבר של רגולריזציית ה הוא קבוע (עד כדי סימן). המשמעות של זה הינה שב כלל שפרמטר מסויים גדול יותר כך הרגולריזציה תתאמץ יותר להקטין אותו ויחסית פחות תשפיע על הפרמטרים הקטנים. מנגד, רגולריזצייית ה תפעל להקטין את כל האיברים ללא קשר לגודלם.
6)
כפי שציינו בסעיף הקודם, רגולריזציית ה תשפיע באופן מועט יחסית על האיברים הקטנים ולא תתאמץ להקטין אותם ובעיקר תפעל להקטין את האיברים הגדולים. מנגד, רגולריזציית ה תמשיך ולנסות להקטין את האיברים כל עוד הם שונים מ-0 ולכן בפועל היא תיטה לאפס יותר איברים.
הערה: בפועל בגלל שגודלו של איבר הרגולריזציה בגרדיאנט של קבוע הוא יקטין את האיברים לערכים קרובים ל-0 ואז יתחיל להתנדנד סביב ה-0.
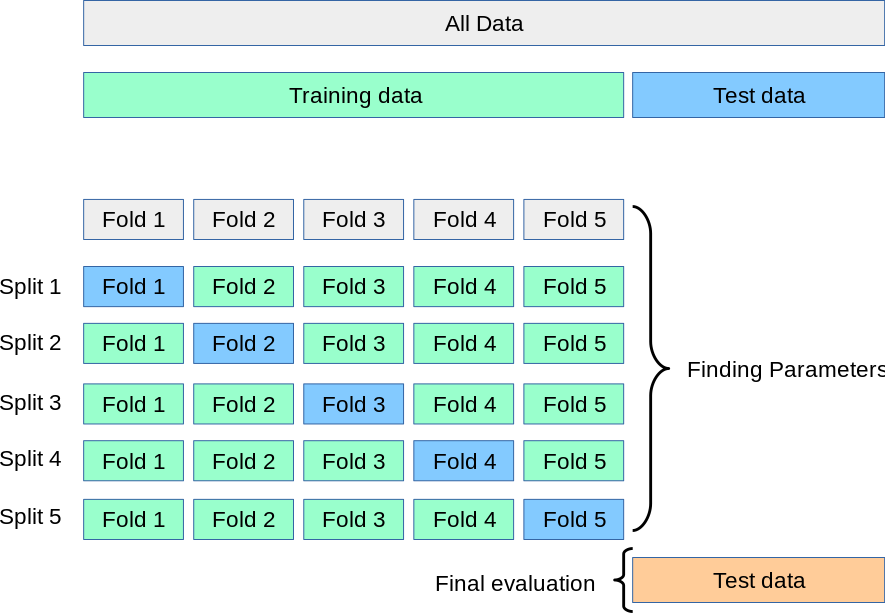
K-fold cross validation
במקרים בהם גודלו של המדגם שנתון לנו הינו קטן לא נוכל להקצות כמות גדולה של דגימות לטובת ה validation set. במקרים כאלה ה validation עלול להיות לא מאד מייצג ולפגוע בבחירה של ה hyper-parmeters. במקרים כאלה נרצה למצוא דרך טובה יותר להעריך את ביצועי המודל בעבור כל בחירה של hyper-parameters. שיטת ה K-fold cross validataion מציעה שיטה לשפר את הדיוק על הערכת הביצועים על ידי מיצוע על כמה validation sets.
בשיטה זו נחלק את ה train set שלנו ל קבוצות ונבצע את הערכת הביצויים פעמים באופן הבא:
- בכל פעם נבחר (על פי הסדר) את אחת הקבוצות לשמש כ validation set הנוכחי.
- בניה של מודל על סמך ה קבוצות האחרות
- חישוב הביצועים של המודל על סמך הקבוצה שנבחרה.
הביצועיים הכוללים יהיו הממוצע של התוצאות אשר התקבלו ב החזרות.
גדולים אופיינים ל הינם בין 5 ל10.
כמו תמיד, לאחר קביעת ה hyper-parameters ניתן לאחד חזרה את כל הקבוצות ל train set אחד ולבנות בעזרתו את המודל תוך שימוש ב hyper-parameters שנבחרו.
להלן סכימה של החלוקה של המדגם בעבור בחירה של (שרטוט זה לקוח מתוך התיעוד של החבילה scikit learn):
Leave-one-out cross validation
במקרים מסויימים (בעיקר כאשר ה train set מאד קטן) אנו נבחר לקחת את להיות שווה למספר האיברים שב train set. במקרה זה גודלה של כל קבוצה יהיה 1. מקרה זה מכונה לרוב Leave-one-out cross validation.
תרגיל 3.3 - בחירת סדר המודל
נתון המדגם הבא:
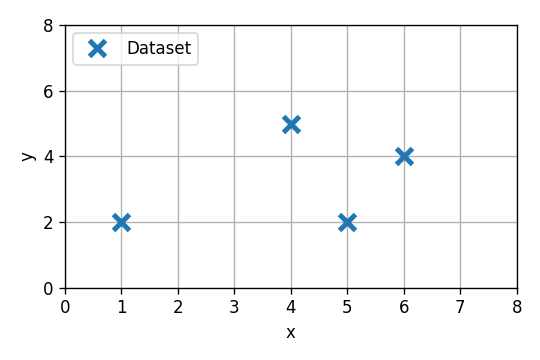
נרצה לנסות ולהתאים למדגם הנתון אחד משני מודלים: מודל לינארי מסדר 0 (פונקציה קבועה) או מסדר ראשון (פונקציה לינארית עם היסט). בתרגיל זה נבחן דרכים לקביעת סדר המודל.
נפצל את המדגם כך ששלושת הדגימות הראשונות יהיו הtrain set והאחרונה תהיה ה test set.
1) השתמשו ב LLS על מנת להתאים כל אחד משני המודלים המוצעים ל train set. העריכו את ביצועי החזאי על פי שגיאת החיזוי המתקבל על הנקודה שב test set. מי מהמודלים נותן ביצועים טובים יותר?
2) מדוע לא נרצה לבחור את סדר המודל על סמך ההשוואה שעשינו על ה test set?
משלב זה והלאה נשכח שביצענו את הערכת הביצועים על ה test set וננסה לקבוע את סדר המודל על סמך validation set.
3) הפרישו מתוך ה train set את הדגימה השלישית על מנת שתשמש כ validation set. התאימו כעת את שני המודלים ל train set החדש והעריכו את ביצועיהם על ה validation set.
4) במקום להשתמש ב validation set קבוע, השתמשו ב leave-one-out על מנת לבחור מבין שני המודלים.
פתרון 3.3
1)
נחלק את המדגם ל train set ו test set:
סדר 0
מודל מסדר 0 (פונקציה קבועה) הוא כמובן מקרה מנוון של מודל לינארי עם מאפיין יחיד של . במקרה זה אנו מצפים כי המודל אשר ימזער את השגיאה הריבועית יהיה פשוט פונקציה קבועה אשר שווה ל הממוצע על ה train set. נראה כי זה אכן הפתרון המתקבל מתוך הפתרון הסגור. בעבור מודל זה המטריצה והוקטור יהיו:
הפרמטר האופטימאלי יהיה:
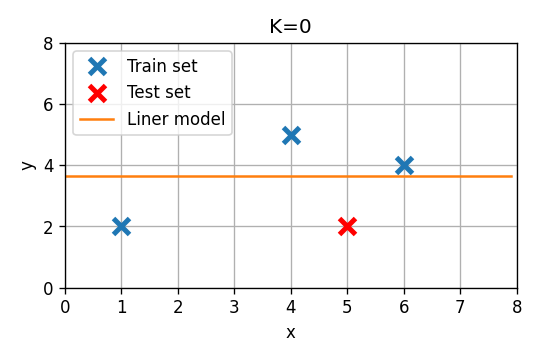
שגיאת החיזוי תהיה במקרה זה .
סדר ראשון
מודל זה הינו מודל לינארי עם המאפיינים:
המטריצה והוקטור יהיו:
הפרמטרים האופטימאלים יהיו:
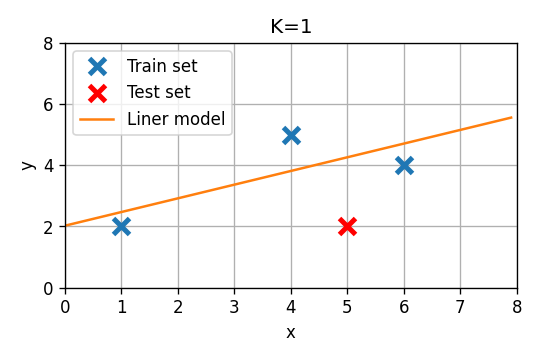
שגיאת החיזוי תהיה במקרה זה .
על סמך שיגאת החיזוי על ה test set נראה שהמודל מסדר 0 עדיף.
2)
תפקידו של ה test set הינו להעריך את ביצועי המודל הסופי לאחר שסיימנו את כל השלבים של בניית המודל כולל בחירת hyper parameters כגון סדר המודל. כאשר אנו מקבלים החלטה כל שהיא או קובעים פרמטר כל שהוא על סמך ה test set אנו למעשה גורמים למודל שלנו להתחיל לעשות overfitting ל test set הספציפי שבידינו ולכן לא נוכל להשתמש בו יותר על מנת לבצע הערכה בלתי מוטית של ביצועי המודל שלנו.
3)
נקצה את הדגימה השלישית במדגם לטובת ה validation set:
נתאים שוב את שני המודלים על סמך ה train set החדש ונעריך את שגיאת החיזוי על ה validation set:
סדר 0
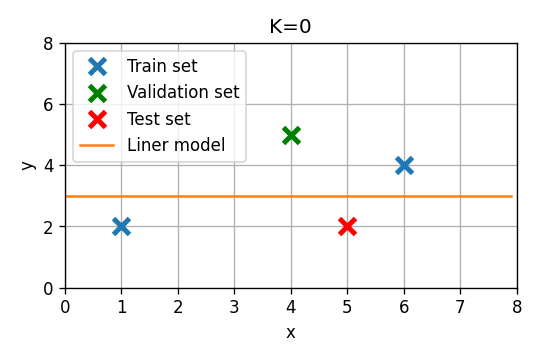
שגיאת החיזוי על ה validation set תהיה במקרה זה .
סדר ראשון
הפרמטרים האופטימאלים יהיו:

שגיאת החיזוי על ה validation set תהיה במקרה זה .
כעת נראה כי דווקא המודל מסדר ראשון הוא המודל העדיף. מכיוון ש ה validation set שלנו במקרה זה קטן מאד הוא לא מאד מייצג, ישנו סיכוי סביר שתוצאה זו התקבלה במקרה ושעל הפילוג האמיתי דווקא המודל מסדר 0 יכליל יותר טוב.
4)
נחזור על הבחירה של סדר המודל בעזרת leave-one-out cross validation. במקרה זה אנו נחזור על החישוב של הסעיף הקודם 3 פעמים כשבכל פעם אנו בוחרים נקודה אחרת מה train set שתשמש כ validation set. את ביצועים של כל אחד מהמודלים נחשב בתור הממוצע על שלושת החזרות.
סדר 0
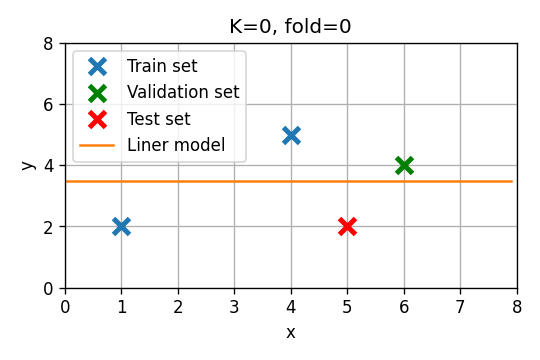
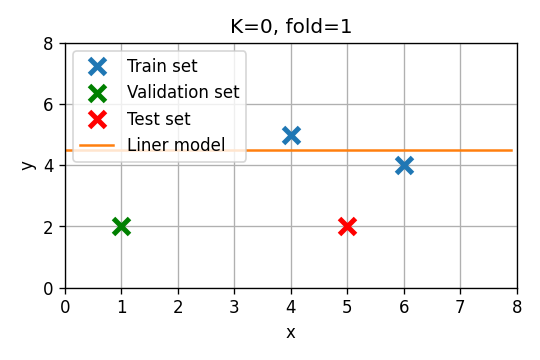
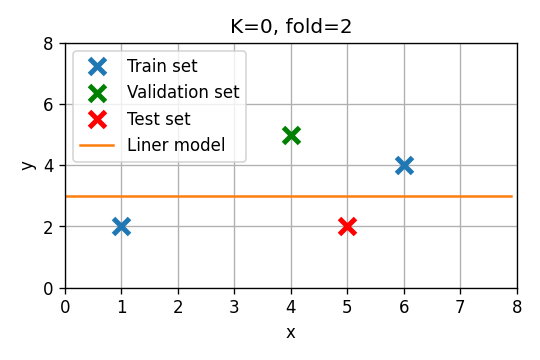
- Fold 0: . שיגאת חיזוי:
- Fold 1: . שיגאת חיזוי:
- Fold 2: . שיגאת חיזוי:
שגיאת חיזוי ממוצעת:
סדר ראשון
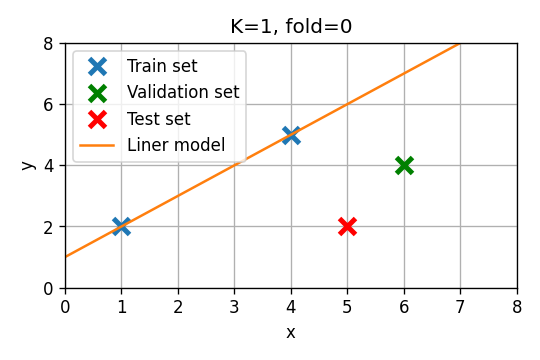
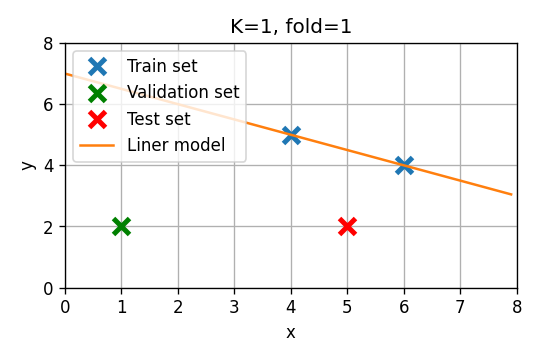
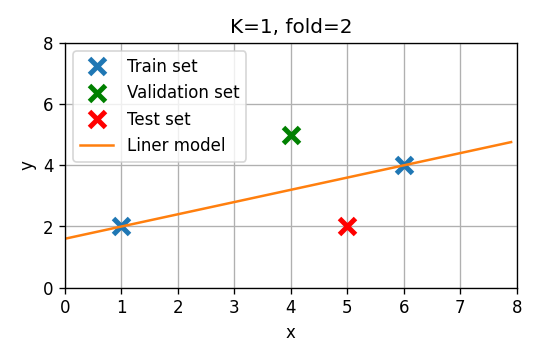
- Fold 0: . שיגאת חיזוי:
- Fold 1: . שיגאת חיזוי:
- Fold 2: . שיגאת חיזוי:
שגיאת חיזוי ממוצעת:
על פי leave-one-out נראה שוב כי המודל מסדר 0 הוא העדיף. מכיוון ששיטה זו לא מסתמכת על נקודה אחת לקביעת סדר המודל ישנו סיכוי טוב יותר שה hyper-parameters אשר נבחרים בשיטה זו יניבו מודל אשר מכליל בצורה טובה יותר
דוגמא מעשית - חיזוי זמן נסיעה של מוניות בניו יורק

נחזור לבעיה מהתרגול הקודם של חיזוי זמן הנסיעה של מונית בניו יורק בעזרת המדגם הבא:
| passenger count | trip distance | payment type | fare amount | tip amount | pickup easting | pickup northing | dropoff easting | dropoff northing | duration | day of week | day of month | time of day | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2 | 2.76806 | 2 | 9.5 | 0 | 586.997 | 4512.98 | 588.155 | 4515.18 | 11.5167 | 3 | 13 | 12.8019 |
| 1 | 1 | 3.21868 | 2 | 10 | 0 | 587.152 | 4512.92 | 584.85 | 4512.63 | 12.6667 | 6 | 16 | 20.9614 |
| 2 | 1 | 2.57494 | 1 | 7 | 2.49 | 587.005 | 4513.36 | 585.434 | 4513.17 | 5.51667 | 0 | 31 | 20.4128 |
| 3 | 1 | 0.965604 | 1 | 7.5 | 1.65 | 586.649 | 4511.73 | 586.672 | 4512.55 | 9.88333 | 1 | 25 | 13.0314 |
| 4 | 1 | 2.46229 | 1 | 7.5 | 1.66 | 586.967 | 4511.89 | 585.262 | 4511.76 | 8.68333 | 2 | 5 | 7.70333 |
| 5 | 5 | 1.56106 | 1 | 7.5 | 2.2 | 585.926 | 4512.88 | 585.169 | 4511.54 | 9.43333 | 3 | 20 | 20.6672 |
| 6 | 1 | 2.57494 | 1 | 8 | 1 | 586.731 | 4515.08 | 588.71 | 4514.21 | 7.95 | 5 | 8 | 23.8419 |
| 7 | 1 | 0.80467 | 2 | 5 | 0 | 585.345 | 4509.71 | 585.844 | 4509.55 | 4.95 | 5 | 29 | 15.8314 |
| 8 | 1 | 3.6532 | 1 | 10 | 1.1 | 585.422 | 4509.48 | 583.671 | 4507.74 | 11.0667 | 5 | 8 | 2.09833 |
| 9 | 6 | 1.62543 | 1 | 5.5 | 1.36 | 587.875 | 4514.93 | 587.701 | 4513.71 | 4.21667 | 3 | 13 | 21.7831 |
בסוף התרגול הקודם השתמשנו במודל מהצורה של
אשר כולל תלות ליניארית במרחק האוירי שאותו צריכה המונית לעבור ותלות ריבועית בקאורדינטה של נקודת תחילת הנסיעה
הערכת הביצועים
נתחיל לחלק את המדגם ל 80% train set ול 20% test set. נשתמש ב train set על מנת לקבוע את הפרמטרים של המודל ונשערך את שגיאת ה RMSE על ה train set ועל ה test set. לאחר חישוב הפרמטרים והערכת הביצועים נקבל:
זאת אומרת שאנו צופים שנדע לחזות את זמן הנסיעה (על נסיעות שלא ראינו לפני) בדיוק של דקות.
מודל פולינומיאלי
ננסה כעת להתאים מודל שהוא פולינום של קורדינטת ההתחלה וקאורדינטת הסיום:
קביעת סדר המודל
על מנת לקבוע את סדר המודל (החזקה המקסימאלית של הפולינום) נשתמש ב validation set. נפצל את ה train set ל 75% train set חדש ו 25% validataion set.
נסרוק כעת את כל המודלים עד לסדר 9, בעבור כל סדר נאמן מודל על ה train set ונחשב את ביצועי המודל על ה validation set. חישוב זה נותן את התוצאה הבאה:
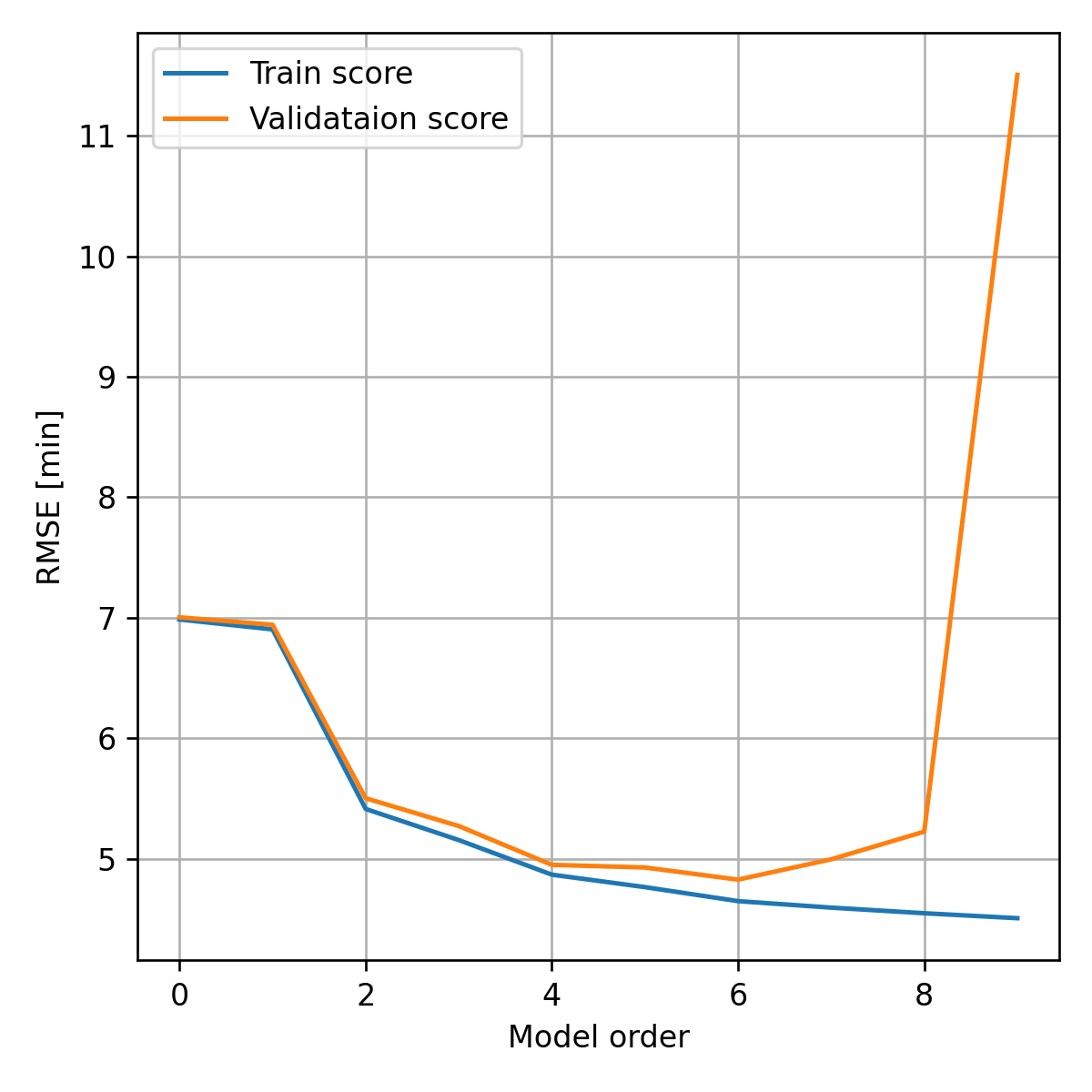
בגרף זה ניתן לראות את ה tradeoff בבחירת סדר המודל ואת תופעת ה overfitting. בקצה השמאלי של הגרף נמצאים המודלים ה"פשוטים" (פונקציה קבועה, פונקציה לינארית וכו') באיזור זה השגיאה העיקרית היא שגיאת הקירוב (או ה bias). בקצה הימני נמצאים פולינומים בעלי מספר רב של מקדמים אשר מסוגלים לקרב מגוון רחב של מודלים. באיזור זה השגיאה העיקרית היא שגיאת השיערוך (או ה variance). אנו נחפש את סדר המודל האופטימאלי אשר נותן את שגיאת ההכללה הנמוכה ביותר. בקירוב זהו הסדר שנותן את הביצועים הטובים ביותר על ה validation set.
על פי תוצאה זו אנו נבחר את סדר המודל להיות 6.
אימון מחדש של המודל
כעת נאחד חזרה את ה validation set וה train set ונאמן מחדש את המודל וזה יהיה המודל הסופי בו נשתמש. נעריך את ביצועי המודל הסופי בעזרת ה test set. חישוב זה נותן תוצאה של:
קיבלנו שיפור של כמעט 10% לעומת המודל שממנו התחלנו.
אופציה אלטרנטיבית - רגולריזציה
ניתן לחילופין לקבע את סדר המודל להיות 9 ולהשתמש באיבר רגולריזציה על מנת למזער את ה overfitting. שימוש ב Ridge regression (רגולריזציית ) נותן את הביצועיים הבאים:
אשר מאד קרובים לביצועים שקיבלנו בעבור מודל מסדר 6.