הרצאה 13 - סיכום

PDF

תהליך פתרון בעיה בלמידה מונחית

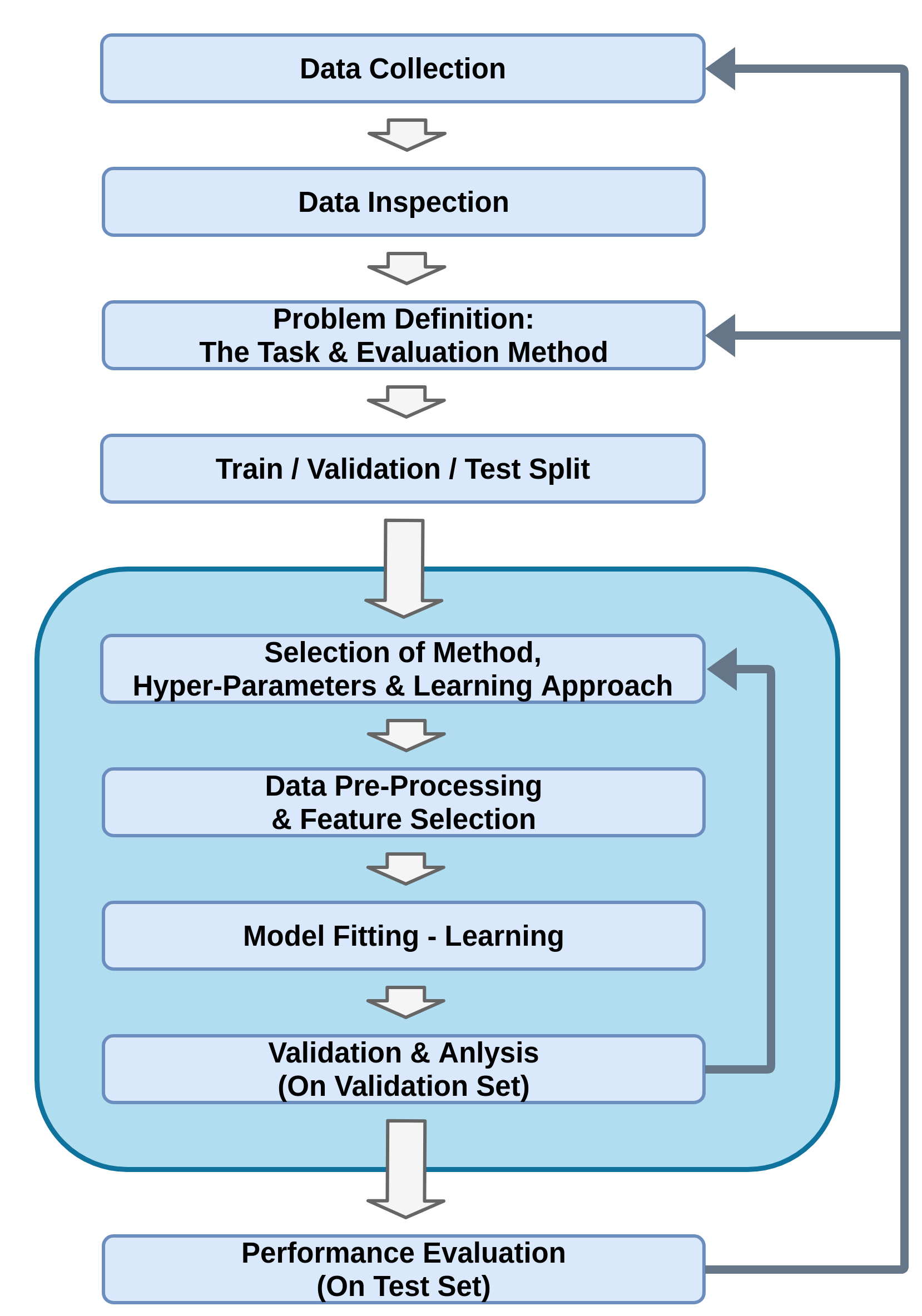
הגדרת הבעיה

ב supervised learning תמיד ננסה למצוא חזאי $\hat{y}=h(\boldsymbol{x})$ .

הפרדנו בין שתי מקרים:

בעיות סיווג (classification): $\text{y}$ דיסקרטי וסופי.
בעיות רגרסיה (regression): $\text{y}$ רציף.

קיימים מקרים בהם מספר התיוגים המותרים לכל קלט גדול מאחד. דוגמה? Multi label problem.

הערכת ביצועים

נגדיר את פונקציית המחיר (cost) שבה נרצה להשתמש בכדי להעריך את החזאי. לרוב נבחר פונקציית מחיר מהצורה:

C(h)=\mathbb{E}\left[l(h(\mathbf{x}),\text{y})\right]

פונקציות מסוג זה מכונות פונקציות סיכון (risk).

הפונקציה $l$ מוכנה פונקציית ההפסד (loss)

מכיוון שהפילוג של $\text{y}$ ו $\mathbf{x}$ לא באמת ידוע לנו אנו נשתמש ב test set ובתוחלת בכדי להעריך את הביצועים.

פונקציות הפסד (פונקציות סיכון) נפוצות

Common For	Loss Name	Risk Name	Loss Function	Optimal Predictor
Classification	Zero-One Loss	Misclassification Rate	$l\left(y_1,y_2\right)=I\left\lbrace y_1\neq y_2\right\rbrace$	$h^*\left(x\right)=\underset{y}{\arg\max}\ p_{\text{y}\mid\mathbf{x}}\left(y\mid x\right)$
Regression	$L_1$	Mean Absolute Error	$l\left(y_1,y_2\right)=\left\vert y_1-y_2\right\vert$	Median: $h^*\left(x\right)=\hat{y}$ $s.t.\ F_{\text{y}\mid\mathbf{x}}\left(\hat{y}\mid x\right)=0.5$
Regression	$L_2$	Mean Squared Error (MSE)	$l\left(y_1,y_2\right)=\left(y_1-y_2\right)^2$	$h^*\left(x\right)=\mathbf{E}\left[\text{y}\mid\mathbf{x}\right]$

שאלה: מתי יש מוטיבציה לפונקציית הפסד שאינה 0-1 במקרה של סיווג? דוגמה?

Discriminative vs. Generative

אנו מבחינים בין 3 גישות אשר משמשות לפתרון בעיות supervised learning:

גישה דיסקרימינטיבית: $\mathcal{D}$ -> $h(\boldsymbol{x})$ .
גישה גנרטיבית: $\mathcal{D}$ -> $p_{\mathbf{x},\text{y}}(\boldsymbol{x},y)$ -> $p_{\text{y}|\mathbf{x}}(y|\boldsymbol{x})$ -> $h(\boldsymbol{x})$ .
גישה דיסקרימינטיבית הסתברותית: $\mathcal{D}$ -> $p_{\text{y}|\mathbf{x}}(y|\boldsymbol{x})$ -> $h(\boldsymbol{x})$ .

שאלה: מתי יש יתרונות יחסיים לגישות השונות?

פירמול הבעיה

במרבית השיטות נשתמש במודל פרמטרי (לחזאי או לפילוג) ונרשום את הבעיה כבעיית אופטימיזציה על הפרמטרים $\boldsymbol{\theta}$ של המודל:

\boldsymbol{\theta}^*=\underset{\boldsymbol{\theta}}{\arg\min}\quad f\left(\boldsymbol{\theta};\mathcal{D}\right) \\

לרוב לא נדע לפתור את הבעיה באופן אנליטי ונשתמש בשיטות אלטרנטיביות למציאת פתרון "סביר".
בדרך כלל משתמשים בגישות מקומיות מבוססות גרדיאנט. גישות אלה מוגבלות בגלל המקומיות של החיפוש. יש דרכים לשפרן, אך אין פתרון אוניברסלי.

Cross-Validation

למרבית השיטות יש מספר hyper-parameters שאינם חלק מבעיית האופטימיזציה שאותם יש לקבוע מראש.

הדרך הנפוצה לבחור hyper-parameters הינה על ידי שימוש ב validation set על מנת לבדוק מספר ערכים שונים ולבחור את אלו אשר נותים את הביצועים הטובים ביותר.

עיבוד מקדים (preprocessing)

במרבית המקרים אנו נרצה לבצע פעולות שונות על המדגם לפני הזנתו לאלגוריתם על מנת להקל על עבודת האלגוריתם.

דוגמאות:

חילוץ מאפיינים שנבחרו באופן ידני: $\boldsymbol{x}_{\text{new}}=\Phi(\boldsymbol{x})$ .
הורדת מימד (על ידי שימוש באלגוריתם כגון PCA).
נרמול: $\boldsymbol{x}_{\text{new}}=\frac{1}{\sigma_{\mathbf{x}}}(\boldsymbol{x}-\mu_{\mathbf{x}})$
אוגמנטציה (לא נלמד בקורס)

התפקיד של ידע מוקדם בלמידה

מושג טכני = inductive bias
ידע מוקדם – כל מה שיודעים על הבעיה לפני קבלת הנתונים
מימוש – הגבלות על מבנה מרחב ההשערות, פונקציית המחיר, אלגוריתם האופטימיזציה
מוטיבציה – שיפור יכולת ההכללה (מניעת התאמת יתר), חסינות לרעש, האצת למידה, "פרשנות" פשוטה יותר של הפתרון

התפקיד של ידע מוקדם בלמידה

דוגמאות

בחירת מאפיינים מושכלת
מבנה הרשת – למשל CNN משקף מבנה של תמונות
רגולריזציה – העדפת מודלים "פשוטים"
העברת ידע מבעיות קודמות (transfer learning) - לא למדנו
הרחבת הנתונים (data augmentation) - לא למדנו

היום – הרבה ידע מוקדם "מסתובב" מפתרונות טובים של בעיות קודמות וניתן להעברה למטלות חדשות. למשל, בנושאים של עיבוד תמונה, עיבוד שפה, חיזוי מבנה חלבונים ועוד הרבה

מעבר על האלגוריתמים שנלמדו בקורס

נעבור במהירות על האלגוריתמים שאותם ראינו בקורס ונבחן את המאפיינים שלהם.

Timeline

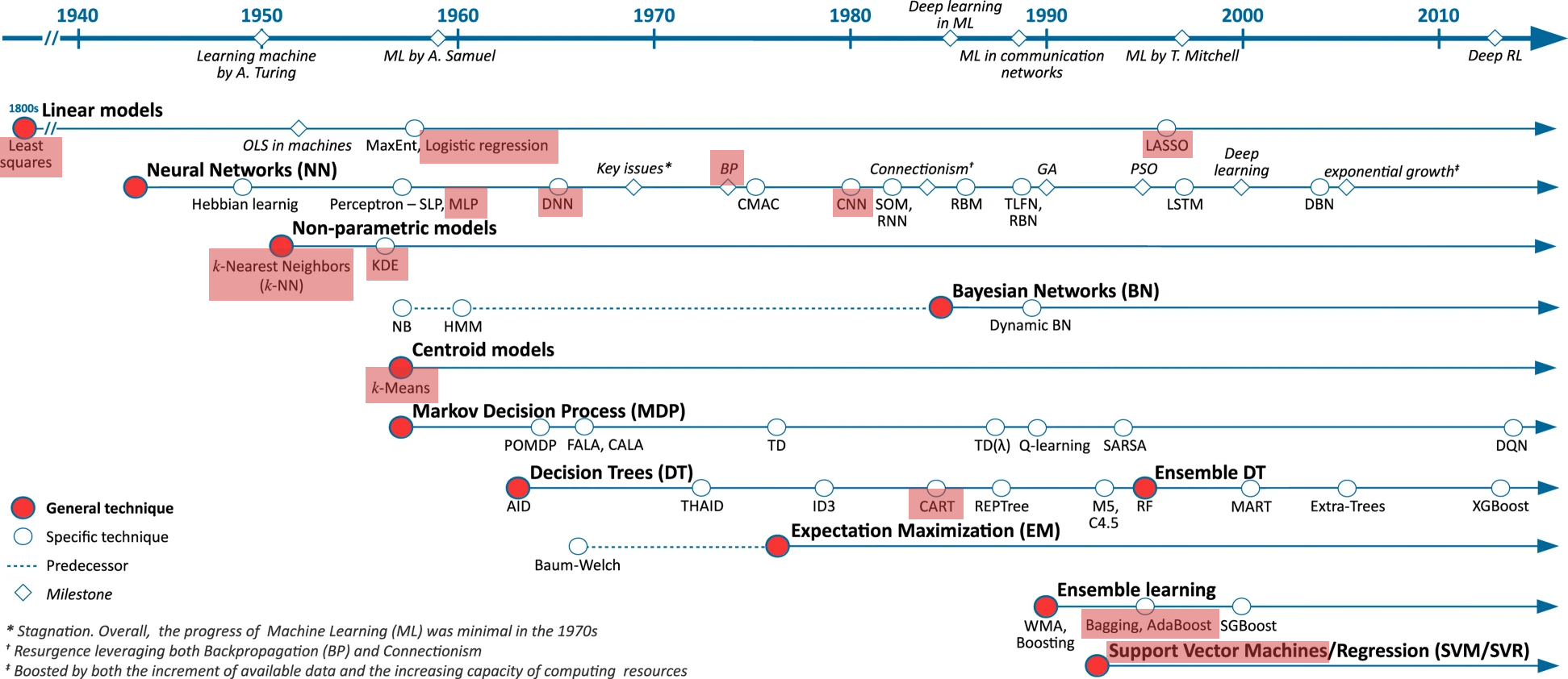
Empirical Risk Minimization

Problem type: Regression (Classifcation)
Approach: Discriminative
Optimization problem: $\boldsymbol{\theta}^*=\underset{\boldsymbol{\theta}}{\arg\min}\ \frac{1}{N}\sum_i l(h(\boldsymbol{x}^{(i)};\boldsymbol{\theta}),y^{(i)})$

Linear Least Squares (LLS)
(also known as ordinary least squares-OLS)

Problem type: Regression with MSE risk
Approach: Discriminative
Model: $h(\boldsymbol{x};\boldsymbol{\theta})=\boldsymbol{\theta}^{\top}\boldsymbol{x}$
Optimization problem: $\boldsymbol{\theta}^*=\underset{\boldsymbol{\theta}}{\arg\min}\ \frac{1}{N}\sum_i (\boldsymbol{\theta}^{\top}\boldsymbol{x}^{(i)}-y^{(i)})^2$
How to solve: Closed-form solution: $\boldsymbol{\theta}=(X^{\top}X)^{-1}X^{\top}\boldsymbol{y}$ .

Ridge Regression
(LLS with Tikhonov Regularization ( $l_2$ ))

Problem type: Regression with MSE risk
Approach: Discriminative
Model: $h(\boldsymbol{x};\boldsymbol{\theta})=\boldsymbol{\theta}^{\top}\boldsymbol{x}$
Hyper-parameter: Regularization coefficient $\lambda$
Optimization: $\boldsymbol{\theta}^*=\underset{\boldsymbol{\theta}}{\arg\min}\ \frac{1}{N}\sum_i (\boldsymbol{\theta}^{\top}\boldsymbol{x}^{(i)}-y^{(i)})^2+\lambda\lVert\boldsymbol{\theta}\rVert_2^2$
Question: what is the motivation for the regularization?
How to solve: $\boldsymbol{\theta}=(X^{\top}X+\lambda I)^{-1}X^{\top}\boldsymbol{y}$ , or using Gradient Descent methods.

Least Absolute Shrinkage and Selection Operator (LASSO)
(LLS with $l_1$ Regularization)

Problem type: Regression with MSE risk
Approach: Discriminative
Model: $h(\boldsymbol{x};\boldsymbol{\theta})=\boldsymbol{\theta}^{\top}\boldsymbol{x}$
Hyper-parameter: Regularization coefficient $\lambda$
Optimization: $\boldsymbol{\theta}^*=\underset{\boldsymbol{\theta}}{\arg\min}\ \frac{1}{N}\sum_i (\boldsymbol{\theta}^{\top}\boldsymbol{x}^{(i)}-y^{(i)})^2+\lambda\sum_j\lvert\theta_j\rvert$
How to solve: Variants of gradient descent (were not presented in the course).

K-Nearest Neighbors (K-NN)

Problem type: Classification (and also regression)
Approach: Discriminative
Hyper-parameter: Number of neighbors $K$ .
Properties: Required amount of data that is exponential in the dimension. Good for low dimensions with a lot of data. Slow runtime.
Questions:
- What is the training process?
- What is the main difference between this method and other parametric methods we have learned?

Decision Trees

Problem type: Classification or regression
Approach: Discriminative
Model: A tree with nodes that threshold a single feature.
Hyper-parameter: Number of nodes.
Optimization:
- Classification: Minimize entropy or the Gini index.
- Regression: Minimize RMSE.
How to solve: Add nodes in a greedy manner + pruning.

Decision Trees - Cont.

Properties:
- Very efficient runtime.
- Usually overfits but can efficiently be combined with bagging or boosting.
- Can work with categorical features.
- More interptable (without ensembles).

Hard SVM

Problem type: Binary classification
Approach: Discriminative
Model: $h(\boldsymbol{x})=\text{sign}(\boldsymbol{w}^T\boldsymbol{x}+b)$
Optimization:

$\begin{aligned} \boldsymbol{w}^*,b^* =\underset{\boldsymbol{w},b}{\arg\min}\quad&\frac{1}{2}\lVert\boldsymbol{w}\rVert^2\\ \text{s.t.}\quad&(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)}+b)y^{(i)}\geq1\quad\forall i \end{aligned}$
How to solve: Numerical convex optimization solvers.
Property: Requires the data to be linearly seperable.

Soft SVM

Problem type: Binary classification
Approach: Discriminative
Model: $h(\boldsymbol{x})=\text{sign}(\boldsymbol{w}^T\boldsymbol{x}+b)$
Hyper-parameter: The slack penalty term $C$ .
Optimization:

$\begin{aligned} \boldsymbol{w}^*,b^*,\{\xi_i\}^*= \underset{\boldsymbol{w},b,\{\xi_i\}}{\arg\min}\quad&\frac{1}{2}\left\lVert\boldsymbol{w}\right\rVert^2+C\sum_{i=1}^N\xi_i \\ \text{s.t.}\quad &y^{(i)}\left(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)}+b\right)\geq1-\xi_i\quad\forall i\\ &\xi_i\geq0\quad\forall i \end{aligned}$

Soft SVM - Cont.

How to solve: Numerical convex optimization solvers.
Property: Can be very efficient when combined with the right kernal using the kernal-trick.

Histogram

Approach: Generative
Model: Piecewise constant probability function.
Hyper-parameter: Bin edges.
How to solve: Count relative number of samples in each bin.
Properties:
- Not very useful for supervised learning.
- Required amount of data is exponential in the dimension.
- Great for quick visualization.

KDE

Approach: Generative
Model: Linear combination of $N$ shifted kernel functions.
Hyper-parameter: The kernel function
Properties:
- Required amount of data is exponential in the dimension. Good for low dimensions with a lot of data.

Linear Discriminant Analysis (LDA)

Problem type: Classification
Approach: Generative
Model: $p_{\mathbf{x}|\text{y}}(\boldsymbol{x}|y)=\frac{1}{\sqrt{(2\pi)^d|\Sigma|}}e^{-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_y\right)^T\Sigma^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_y\right)}$
Optimization: MLE (or MAP)
How to solve: Has a closed-form solution.
Properties:
- Linear separation lines.
- Good when each class is concentrated in a different area of the feature space.
- Can deal with classes with very few examples (even 1).

Quadric Discriminant Analysis (QDA)

Problem type: Classification
Approach: Generative
Model: $p_{\mathbf{x}|\text{y}}(\boldsymbol{x}|y)=\frac{1}{\sqrt{(2\pi)^d|\Sigma_y|}}e^{-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_y\right)^T\Sigma_y^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_y\right)}$
Optimization: MLE (or MAP)
How to solve: Has a closed-form solution.
Properties:
- Quadric separetion lines.
- Good when each class is concentrated in a different area of the feature space.

Logistic Regression

Problem type: Classification
Approach: Probabilistic Discriminative
Model: $p_{\text{y}|\mathbf{x}}(y|\boldsymbol{x})=\text{softmax}(F(\boldsymbol{x};\boldsymbol{\theta}))_y=\frac{e^{f_y(\boldsymbol{x};\boldsymbol{\theta}_y)}}{\sum_c e^{f_c(\boldsymbol{x};\boldsymbol{\theta}_c)}}$
Hyper-parameter: The functions $f_y(\boldsymbol{x};\boldsymbol{\theta}_y)$ .
Optimization: MLE (or MAP)
How to solve: Gradient descent.

Linear Logistic Regression

Problem type: Classification
Approach: Probabilistic Discriminative
Model: $p_{\text{y}|\mathbf{x}}(y|\boldsymbol{x})=\text{softmax}(\Theta\boldsymbol{x})_y=\frac{e^{\boldsymbol{\theta}_y^{\top}\boldsymbol{x}}}{\sum_c e^{\boldsymbol{\theta}_c^{\top}\boldsymbol{x}}}$
Hyper-parameter: The matrix $\Theta$ .
Optimization: MLE (or MAP)
How to solve: Gradient descent.

Multi-Layer Perceptron (MLP)

Problem type: Either
Approach: Probabilistic Discriminative / Discriminative
Model: A neural network of fully connected layers.
Hyper-parameter: The number of layers and their width + activation functions.
Optimization:
- Classification: MLE (or MAP)
- Regression: ERM
How to solve: Stochastic Gradient descent (and variants) + backpropogation.
Property: Requires large amounts of data in order to avoid overfiting.

Convolutional Neural Network (CNN)

Problem type: Either
Approach: Probabilistic Discriminative / Discriminative
Model: A NN of convolutional + fully connected layers.
Hyper-parameter: The architecture.
Optimization:
- Classification: MLE (or MAP)
- Regression: ERM
How to solve: Gradient descent + backpropogation.
Property: Very efficient when $\boldsymbol{x}$ has some spatial structure (e.g. images).

Bagging and Boosting

בנוסף לכל השיטות הנ"ל ראינו גם כיצד ניתן לשלב מספר חזאים באופן הבא:

בעזרת Bagging בכדי להקטין את ה variance (overfitting) של החזאים.
בעזרת AdaBoost בכדי להקטין את ה bias (underfitting) של החזאים.

מה הלאה - קורסים?

קורסים נוספים בפקולטה בתחום:

046202 - עיבוד וניתוח מידע (unsupervised).
046211 - למידה עמוקה.
046203 - תכנון ולמידה מחיזוקים (reinforcment).
046746 - אלגוריתמים ויישומים בראיה ממוחשבת.
046853 - .ארכיטקטורות מחשבים מתקדמות

מה הלאה - Deep learning?

הכרת טכניקות ספציפיות ברשתות נוירונים (ארכיטקטורות, אופטימיזציות, רגולריזציה וכו'):

מאד דינמי ומשתנה בקצב גבוה.
משתנה מבעיה לבעיה.
הכי טוב זה לקחת בעיה ולראות מה השיטות בהם משתמשים כיום בכדי לפתור אותה.
Google is your friend ...

מה הלאה - צבירת נסיון?

התחום של מערכות לומדות דורש המון נסיון ואינטואיציה שנרכשים עם הזמן.

פרוייקט בתחום.
Kaggle.

חברי סגל בתחום

אביב תמר
איילת טל
גיא גלבוע
דניאל סודרי
יואב שכנר
יניב רומנו
כפיר לוי

ליהי צלניק-מנור
נחום שימקין
ענת לוין
רון מאיר
שי מנור
תומר מיכאלי

הרצאה 13 - סיכום

תהליך פתרון בעיה בלמידה מונחית

הגדרת הבעיה

הערכת ביצועים

פונקציות הפסד (פונקציות סיכון) נפוצות

Discriminative vs. Generative

פירמול הבעיה

Cross-Validation

עיבוד מקדים (preprocessing)

התפקיד של ידע מוקדם בלמידה

התפקיד של ידע מוקדם בלמידה

מעבר על האלגוריתמים שנלמדו בקורס

Timeline

Empirical Risk Minimization

Linear Least Squares (LLS)(also known as ordinary least squares-OLS)

Ridge Regression(LLS with Tikhonov Regularization (l2l_2l2​))

Least Absolute Shrinkage and Selection Operator (LASSO)(LLS with l1l_1l1​ Regularization)

K-Nearest Neighbors (K-NN)

Decision Trees

Decision Trees - Cont.

Hard SVM

Soft SVM

Soft SVM - Cont.

Histogram

KDE

Linear Discriminant Analysis (LDA)

Quadric Discriminant Analysis (QDA)

Logistic Regression

Linear Logistic Regression

Multi-Layer Perceptron (MLP)

Convolutional Neural Network (CNN)

Bagging and Boosting

מה הלאה - קורסים?

מה הלאה - Deep learning?

מה הלאה - צבירת נסיון?

חברי סגל בתחום

מקווה שנהנתם ...

Linear Least Squares (LLS)
(also known as ordinary least squares-OLS)

Ridge Regression
(LLS with Tikhonov Regularization ( $l_2$ ))

Least Absolute Shrinkage and Selection Operator (LASSO)
(LLS with $l_1$ Regularization)