הרצאה 11 - CNN

Stochastic and Mini-Batch Gradient Descent

צעד העדכון ב gradient descent נתון על ידי:

$$\boldsymbol{\theta}^{(t+1)}=\boldsymbol{\theta}^{(t)}-\eta\nabla_{\boldsymbol{\theta}}g(\boldsymbol{\theta}^{(t)})$$

כאשר $g(\boldsymbol{\theta})$ היא פונקציית ה objective שאותה אנו מעוניינים למזער. בהקשר של מערכות לומדות פונקציה זו תכיל לרוב סכום או ממוצע על כל הדגימות במדגם. בקורס זה נתקלנו בשתי בעיות האופטימיזציה הבאות למציאת פרמטרים של מודל:

1. ב ERM אנו רוצים למזער את התוחלת האמפירית של ה risk בעבור חזאי פרמטרי כל שהוא $\hat{y}=h(\boldsymbol{x^{(i)}};\boldsymbol{\theta})$

   $$\underset{\boldsymbol{\theta}}{\arg\min} \underbrace{\frac{1}{N}\sum_{i=1}^N l(h(\boldsymbol{x^{(i)}};\boldsymbol{\theta}),y^{(i)})}_{g(\boldsymbol{\theta};\mathcal{D})}$$

2. MLE, כאשר אנו ממזערים את ה מינוס log-likelihood בעבור פונקציית פונקציית פילוג כל שהיא $p_{\text{y};\mathbf{x}}(y|\boldsymbol{x};\boldsymbol{\theta})$ (לקחנו כאן את המקרה של מקבל בגישה הדיסקרינימניטבית הסתברותית):

   $$\underset{\boldsymbol{\theta}}{\arg\min} \underbrace{-\sum_{i=1}^N \log(p_{\text{y}|\mathbf{x}}(y^{(i)}|\boldsymbol{x}^{(i)};\boldsymbol{\theta})}_{g(\boldsymbol{\theta};\mathcal{D})}$$

במקרים אלו גם הגרדיאנט יכיל סכום על כל המדגם. כאשר המדגם מאד גדול הסכימה יכולה להיות מאד בעייתית וארוכה לחישוב במקרים כאלה נרצה להשתמש בחישוב אלטרנטיבי אשר משתמש בכל צעד רק בחלק מן המדגם ולא בכולו.

Stochastic Gradient Descent

Stochastic Gradient Descent מחשב בכל פעם את הנגזרת על פי דגימה בודדת מתוך המדגם, בלי סכימה בכלל, כאשר בכל צעד נשתמש בדגימה אחרת. שתי אופציות לבחירה של הדגימה בכל צעד הינן:

1. בכל צעד להגריל דגימה אקראית אחרת
2. לעבור על הדגימות במדגם בצורה סידרתית (במקרה זה חשוב לרוב לערבב את הסדר של דגימות)

ההיגון מאחורי שיטה זו הוא שאומנם הנגזרת לפי כל אחת מהדגימות תצביע לכיוון שונה מהנגזרת של הסכום אבל בממוצע על פני כל הדגימות הכיוון הכללי יהיה זהה לכיוון של הנגזרת של הסכום.

היתרון של שיטה זו הוא שהחישוב הוא מאד מהיר שכן במקום סכום על כל המדגם אנו צריכים לחשב את הנגזרת רק בעבור דגימה בודדת, אך החיסרון של שיטה זו הוא שהכיוון של הגרדיאנט יהיה מאד "רועש" ואנו נצטרך לעשות צעדים מאד קטנים שהאלגוריתם באמת יתקדם בכיוון הנכון.

Mini-Batch Gradient Descent

Mini-batch gradient descent הוא פתרון ביניים בין stochastic gradient descent וה gradient descent הרגיל. בשיטה זו נשתמש בקבוצת דגימות מתוך המדגם המכונה mini-batch על מנת לחשב את הנגזרת. בכל צעד אנו נחליף את ה mini-batch. גירסא זו של האלגוריתם היא הנפוצה ביותר לאימון של רשתות נוירונים כאשר גדלים אופיינים של ה mini-batch הינם 32-256 דגימות.

שמות

• Epoch: כאשר אנו עוברים על המדגם באופן סידרתי עם stochastic gradient descent או עם mini-batch gradient descent אנו נגיד שהשלמנו epoch בכל פעם שנסיים מעבר מלא על כל המדגם והתחנו מהתחלה.
• למרות שברוב הספרי הלימוד רבים מתייחסים ל batch כמדגם כולו, בפועל ביום יום משתמשים בשם batch כדי להתייחס ל mini-batch.
• החבילות של machine learning בהם ממומש אלגוריתם המימוש של gradient descent מופיע תחת השם stochastic gradient descent למרות שבפועל ניתן להשתמש בו לכל אחד מהמימושים שציינו (stochastic, mini-batch ורגיל).

עצירה מוקדמת של gradient descent

מסתבר שדרך מוצלחת נוספת למנוע overfitting הינה לעצור את אלגוריתם הגרדיאנט לפני שהוא מתכנס. הדרך לעשות זאת הינה לבדוק את הערך של ה objective על ה validation set לאורך כל תהליך ההתכנסות של אלגוריתם ה gradient descent ולשמור תמיד בצד את הפרמטרים אשר נותנים את ה objective הנמוך ביותר על ה validation set.

גרף אופייני של ה objective במהלך הריצה של אלגוריתם ה gradient descent יראה כך:

Convolutional Neural Networks (CNN)

בהרצאה הקודם הצגנו את ארכיטקטורת ה MLP. כפי שראינו ניתן להגדיל את היכולת הייצוג של הארכיטקטורה על ידי הגדלת הרשת (מספר השכבות והרוחב שלהם). הבעיה היא, שכפי שקורה בכל מודל פרמטרי, הגדלה של יכולת הייצוג תגדיל גם את ה overfitting שהמודל יעשה. באופן כללי רשת בעלת ארכיטקטורה טובה היא לאו דווקא רשת בעלת יכולת ייצוג גבוהה אלא דווקא רשת בעלת יכולת ייצוג נמוכה אשר עדיין מוסגלת לקרב בצורה טובה את הפונקציה שאותה היא מנסה למדל (למשל את החזאי האופטימאלי ב ERM או את הפילוג המותנה בגישה הדיסקרימינטיבת הסתברותית).

מסתבר שישנם בעיות רבות שבהם ארכיטקטורה אשר נקראת convolutional nerual network (CNN) עונה בדיוק על דרישות אלו. ארכיטקטורה זו מבוססת על שכבות הנקראות שכבות קונבולוציה. נסביר ראשית כיצד שכבות אלו פועלות ואחר כך נסביר לאילו מקרים הם טובות.

שכבת קונבולוציה

שכבה קונבולוציה דומה לשכבת fully connected (FC) אך היא נבדלת ממנה בשני מובנים:

1. כל נוירון בשכבה זו מוזן רק מכמות מוגבלת של ערכים הנמצאים בסביבתו הקרובה (בשרטוט המוצג כל נוירון מוזן מ3 ערכים: זה שנמצא מולו, אחד לפני ואחד אחרי).
2. כל הנוירונים בשכבה מסויימת זהים, זאת אומרת שהם משתמשים באותם המשקלים (תכונה המכונה weight sharing).

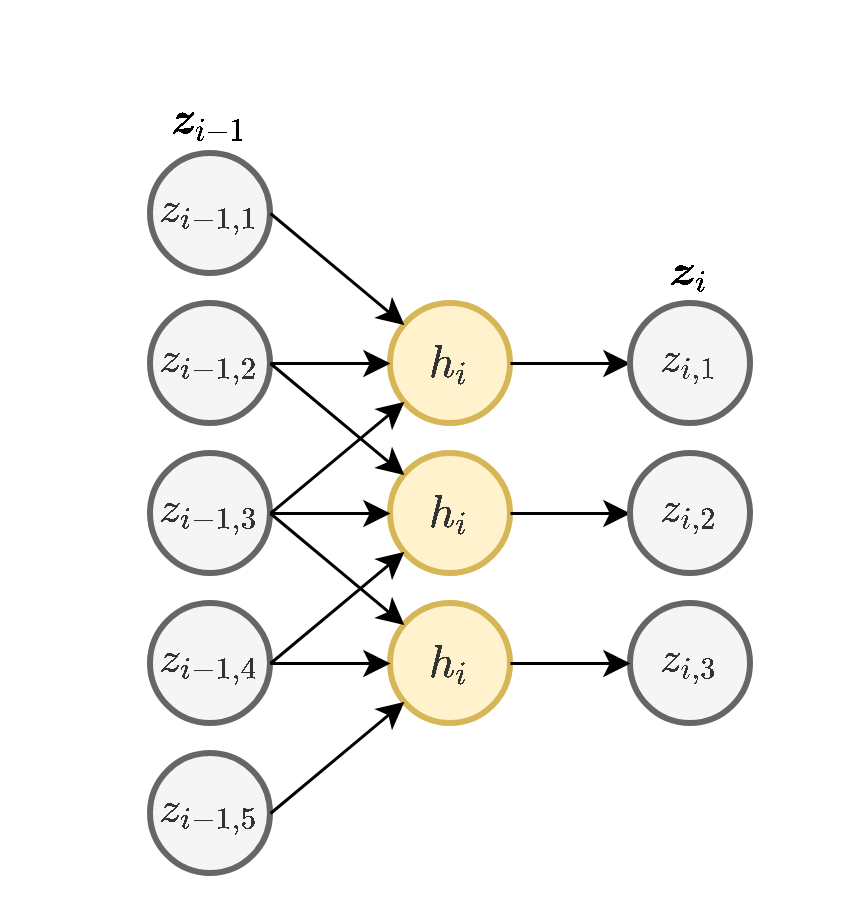
שכבת קונבולוציה היא מקרה פרטי של שיכבת FC שבה כל הקשרים שלא מופיעים בשכבת הקונבולוציה הם 0 ושהמשקולות שלא התאפסו בכל נוירון הם בעות ערכים זהים בין כל הנורונים.

למעשה ניתן לחשוב על הפעולה שאותה מבצע הנוירון כאילו הוא נע לאורך הערכים שבכניסה לשיכבה ומפעיל את הפונקציה שלו כל פעם על סט ערכים אחר:

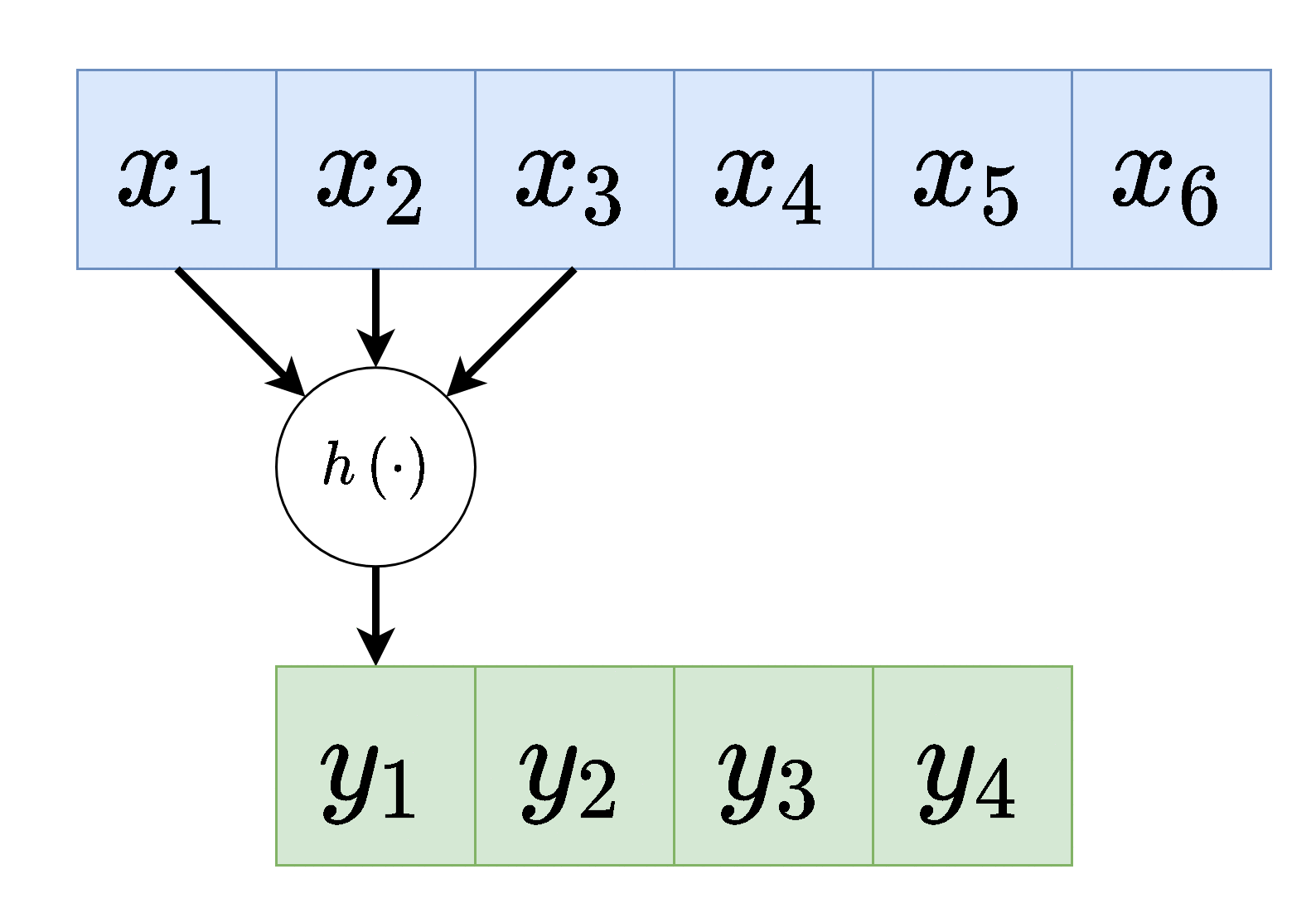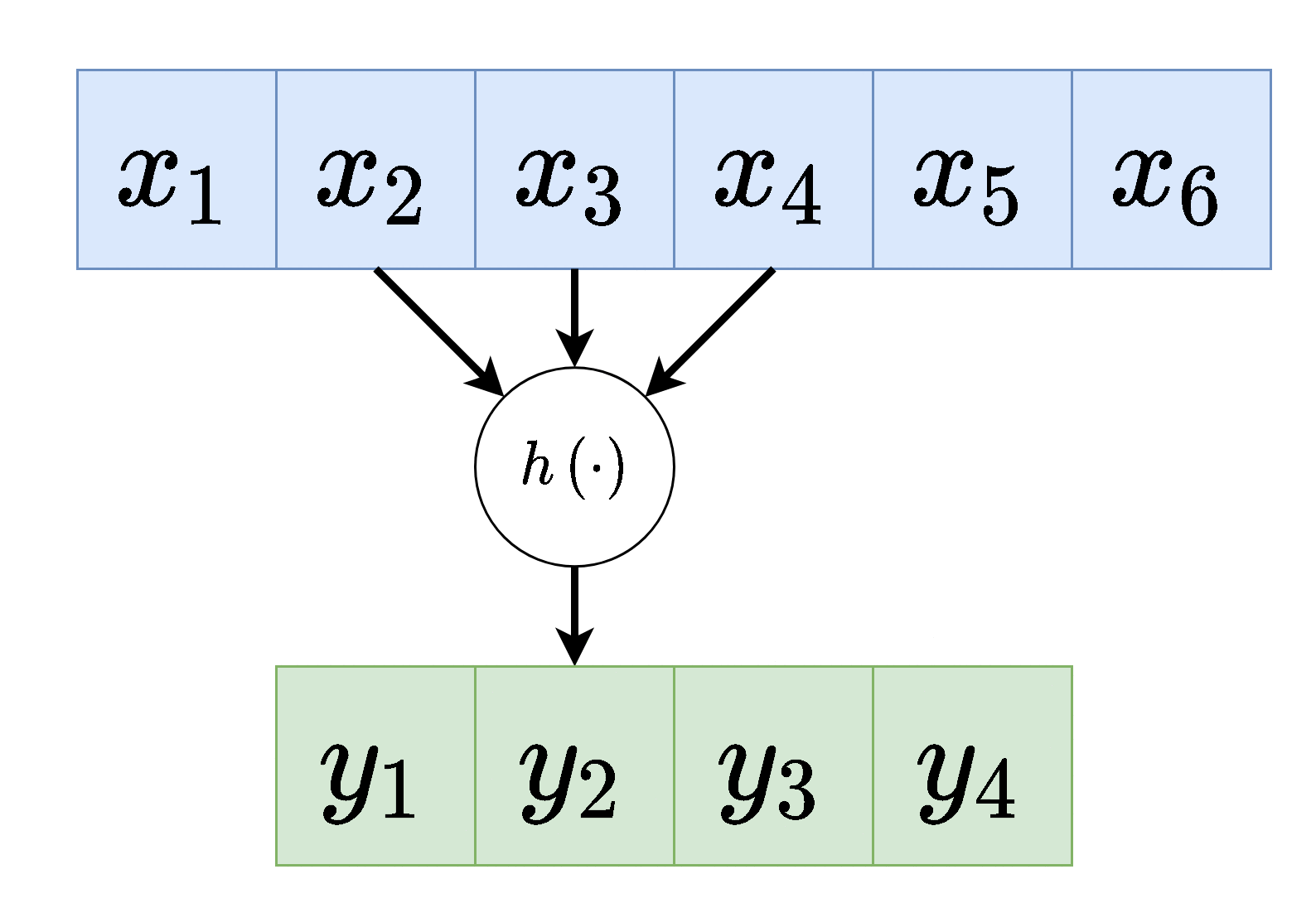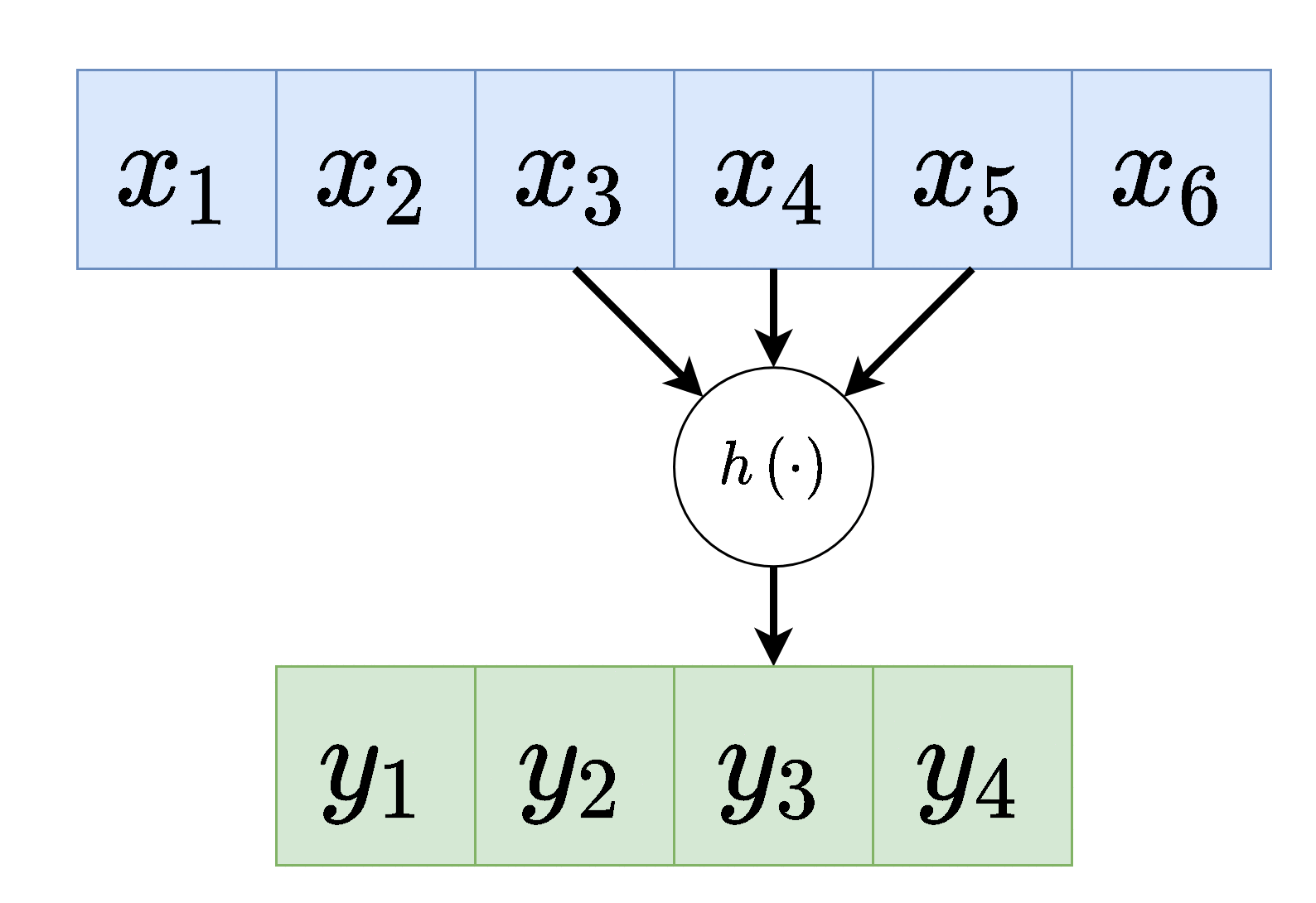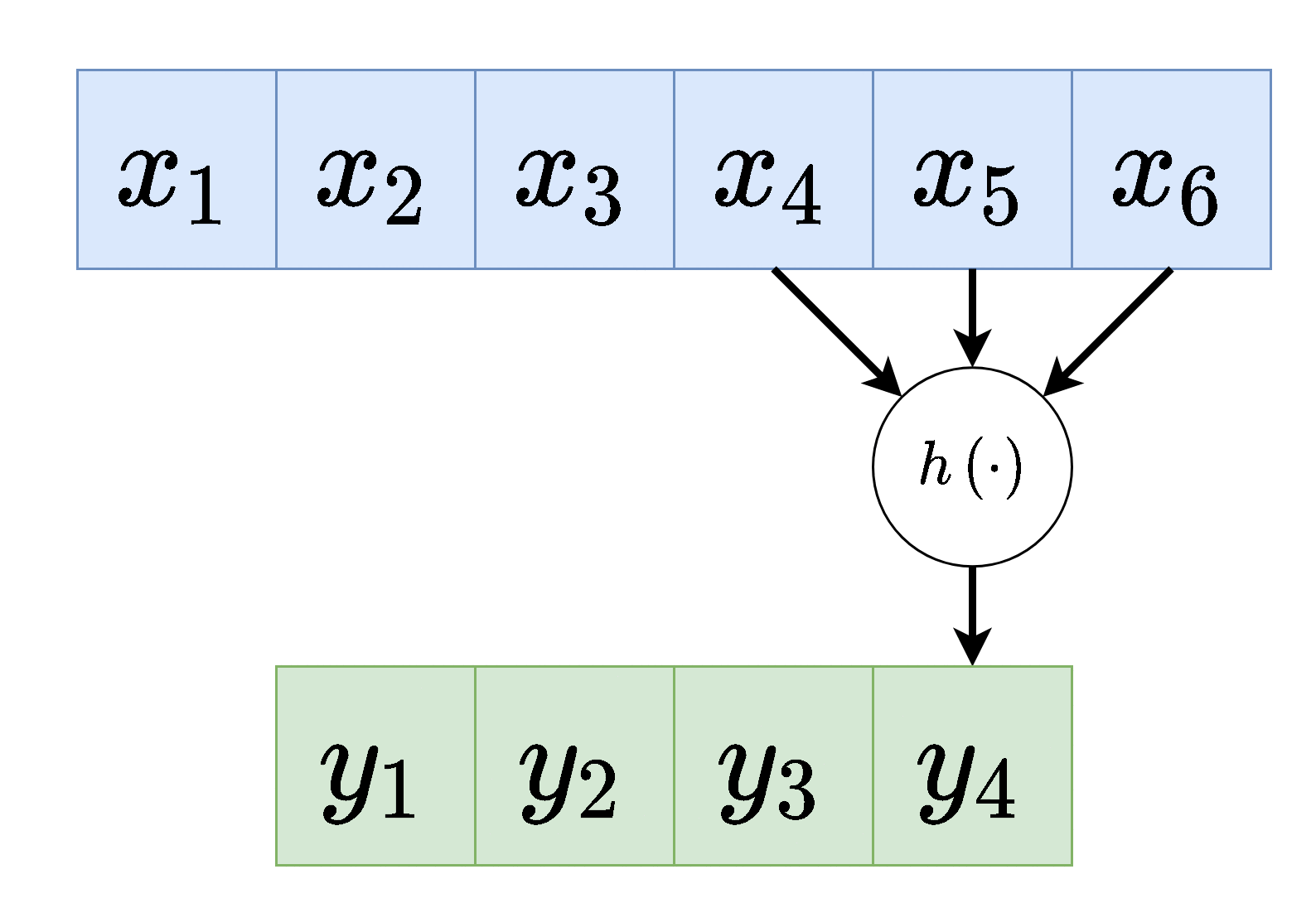
(לשם הפשטות כאן סימנו את הכניסה לשכבה ב $\boldsymbol{x}$ ואת המוצא ב $\boldsymbol{y}$ והשמטנו את האינדקס של השכיבה $i$.)

מתמטית השיכבה מבצעת את שלוש הפעולות הבאות:

1. פעולת קרוס-קורלציה (ולא קונבולוציה) בין וקטור הכניסה $\boldsymbol{x}$ ווקטור משקולות $\boldsymbol{w}$ באורך $K$.
2. הוספת הסט $b$ (אופציונלי).
3. הפעלה של פונקציית הפעלה על וקטור המוצא איבר איבר.

פעולת הקרוס-קורלציה מוגדרת באופן הבא:

$$y_i=\sum_{m=1}^K x_{i+m-1}w_m$$

וקטור המשקולות של שכבת הקונבולציה $\boldsymbol{w}$ נקרא גרעין הקונבולוציה (convolution kernel).

(שימו לב שבניגוד לשמה, שכבת הקונבולוציה מבצעת קורלציה ולא קונבולוציה. ההבדלים בין השתי הפעולות במקרה זה רק עניין של הדרך בה ממספרים את האיברים בוקטור $\boldsymbol{w}$, בקונבולוציה יש להפוך קודם את סדר האיברים בוקטור ורק אז לחשב את הקורלציה).

גודל המוצא של שכבת הקונבולוציה הוא קטן יותר מהכניסה והוא נתון על ידי $D_{\text{out}}=D_{\text{in}}-K+1$.

משום ששכבת הקונבולוציה היא מקרה פרטי מאד מצומצם של שכבת FC יכולת הייצוג שלה קטנה בהרבה. מקובל להסתכל על כמות הפרמטרים של מודל מסויים בתור הערכה גסה ליכולת הייצוג שלו. נשווה בין כמות הפרמטרים בשכבת FC ובשכבת קונבולוציה. נסתכל על שכבת קונבולוציה עם גרעין באורך $K=3$ הפועל על כניסה באורך 10. המוצא של שכבה זו יהיה באורך 8, בשיכבה יהיו ארבעה פרמטרים, שלוש המשקולות שבגרעין ועוד איבר היסט יחיד. לעומת זאת בשכבת FC המחברת כניסה באורך 10 עם מוצא באורך 8 יהיו $8\times10=80$ משקולות אשר קובעות את הקומבינציה הלינארית בכל נוירון ועוד 8 איברי היסט עבור כל אחד מהנוירונים. ניתן לראות אם כן שבשכבת הקונבולוציה יש משמעותית הרבה פחות פרמטרים.

באופן כללי, בשכבת FC קיימות $D_{\text{in}}\times D_{\text{out}}$ משקולות ועוד $D_{\text{out}}$ איברי היסט. לעמות זאת, בשכבת קונבולציה יש $K$ משקולות ואיבר היסט בודד.

קלט רב-ערוצי

במקרים רבים נרצה ששכבת הקונבולציה תקבל קלט רב ממדי, לדוגמא, תמונה בעלת שלושה ערוצי צבע או קלט שמע ממספר ערוצי הקלטה. מבנה זה מאפשר לאזור מרחבי בקלט להכיל אינפורמציה ממספר ערוצי כניסה.

במקרים אלו הניורון $h$ יהיה פונקציה של כל ערוצי הקלט:

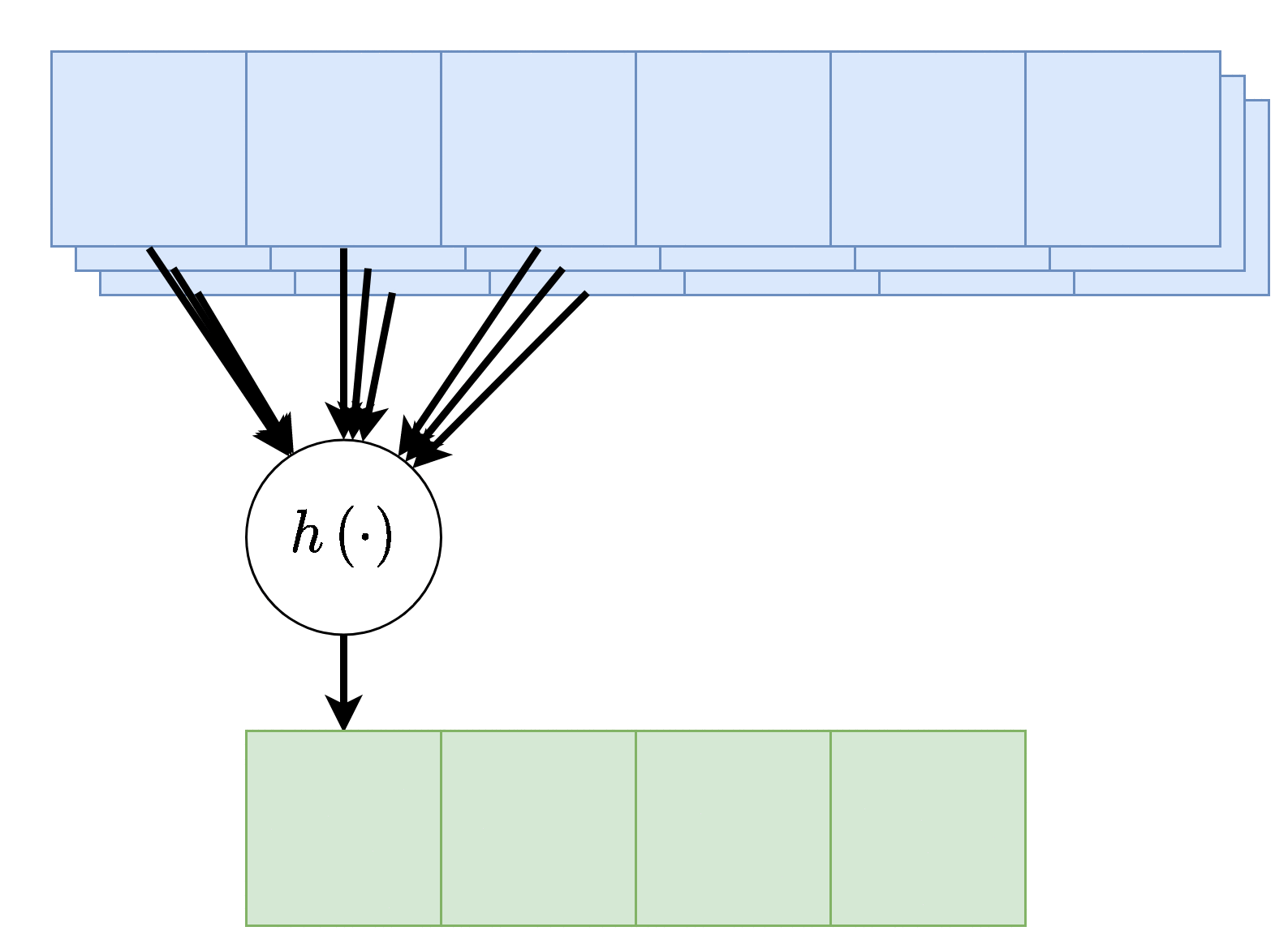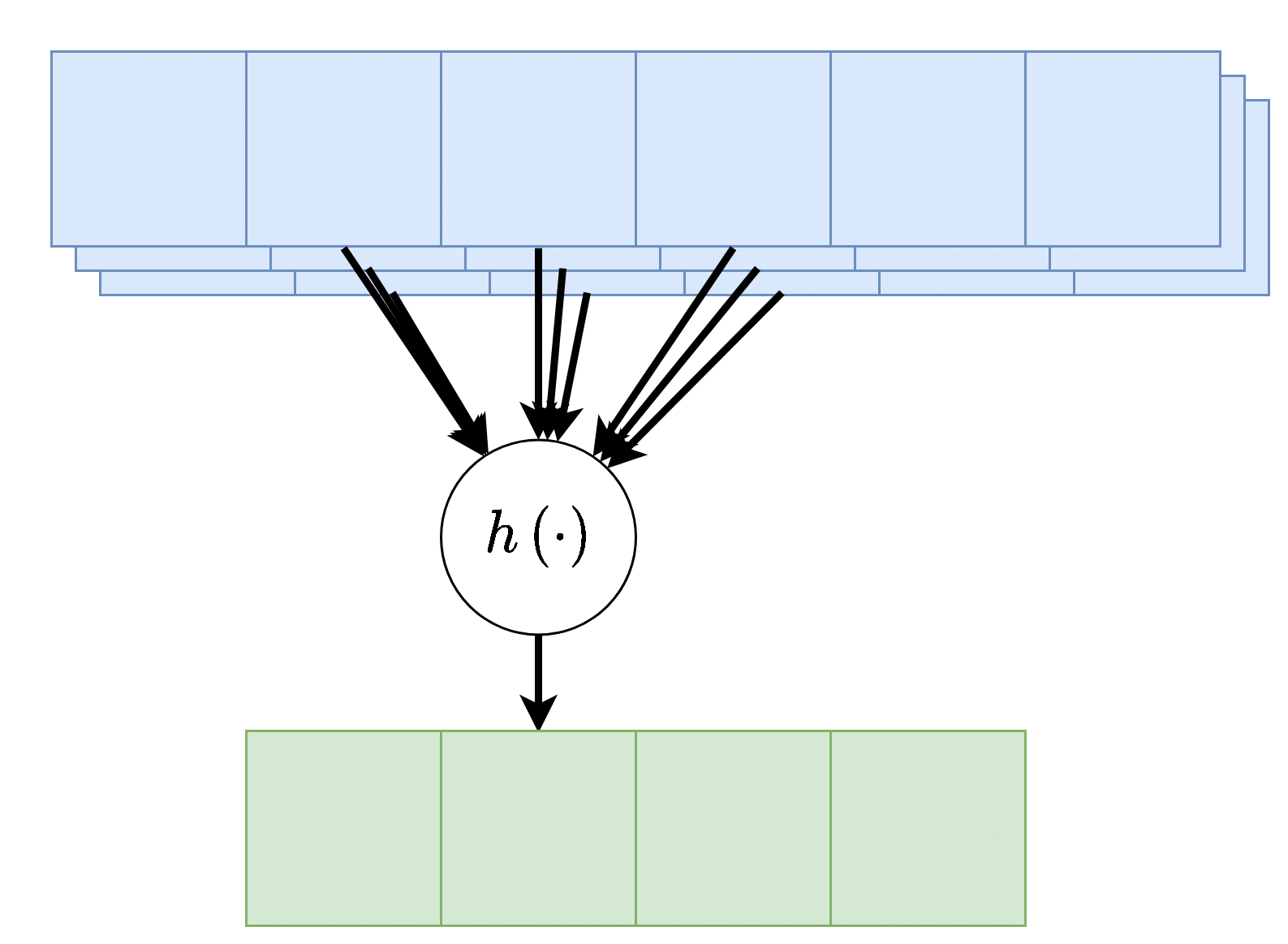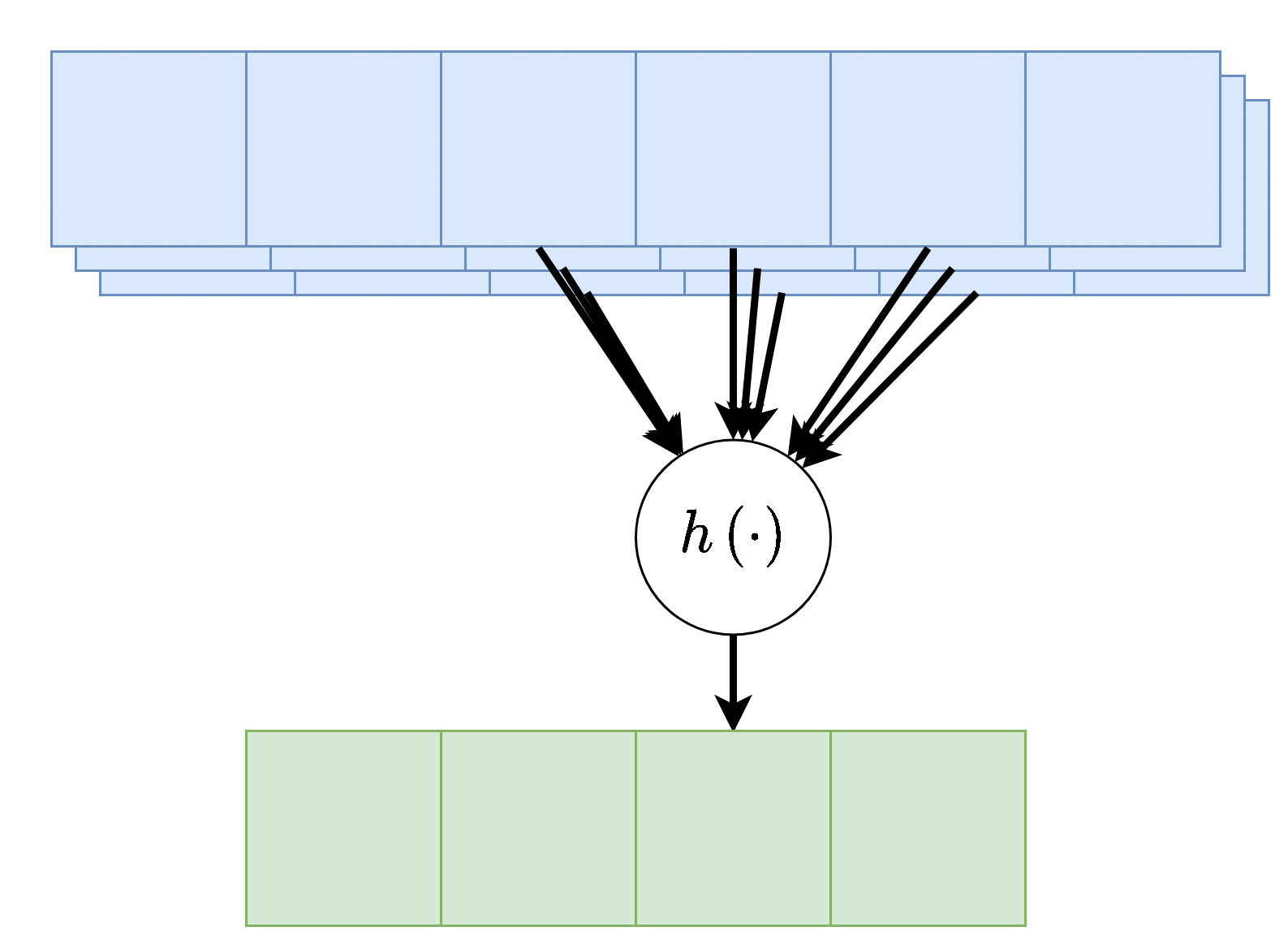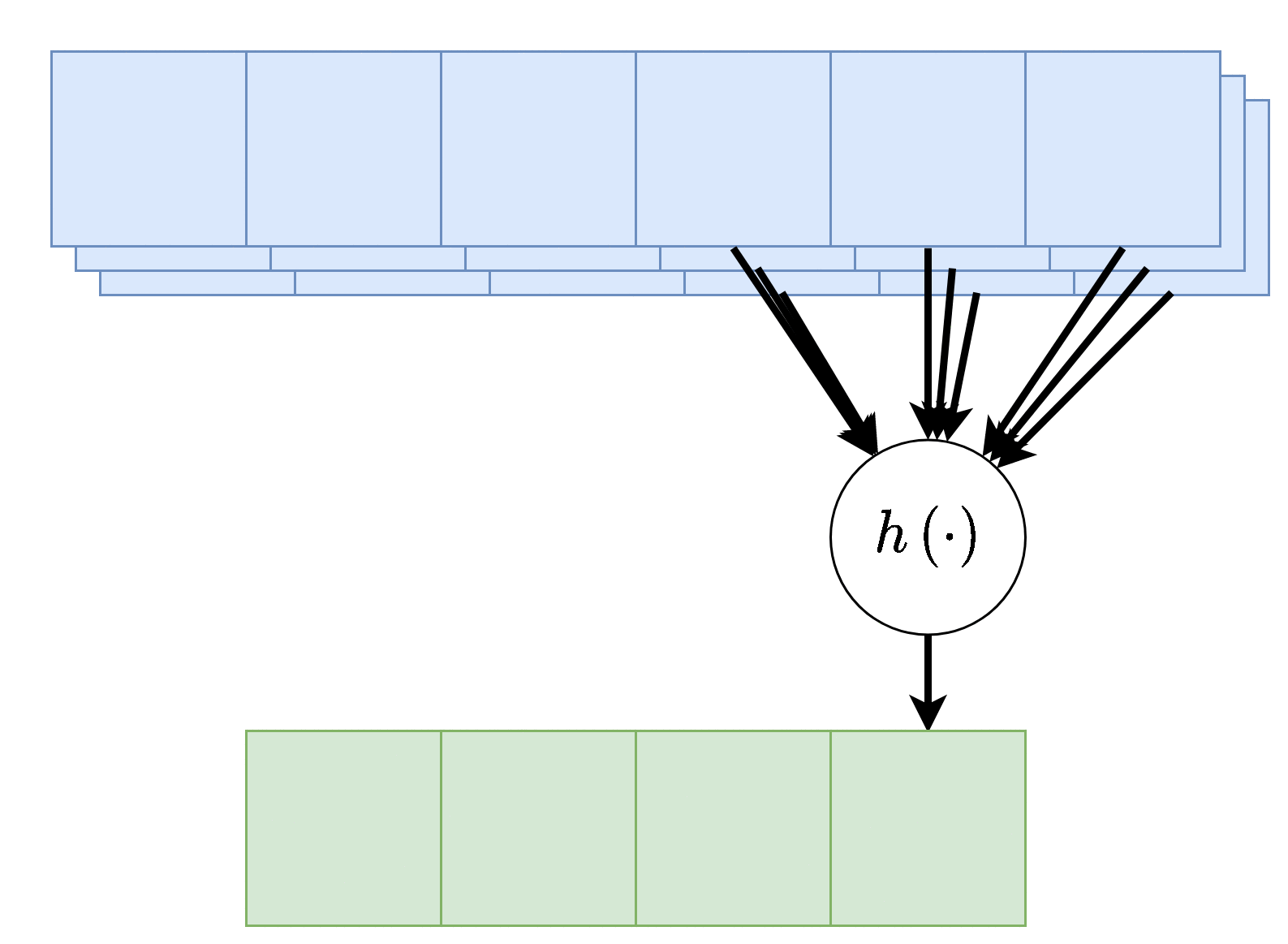
פלט רב-ערוצי

בנוסף, נרצה לרוב להשתמש ביותר מגרעין קונבולוציה אחד, במקרים אלו נייצר מספר ערוצים ביציאה בעבור כל אחד מגרעיני הקונבולוציה.

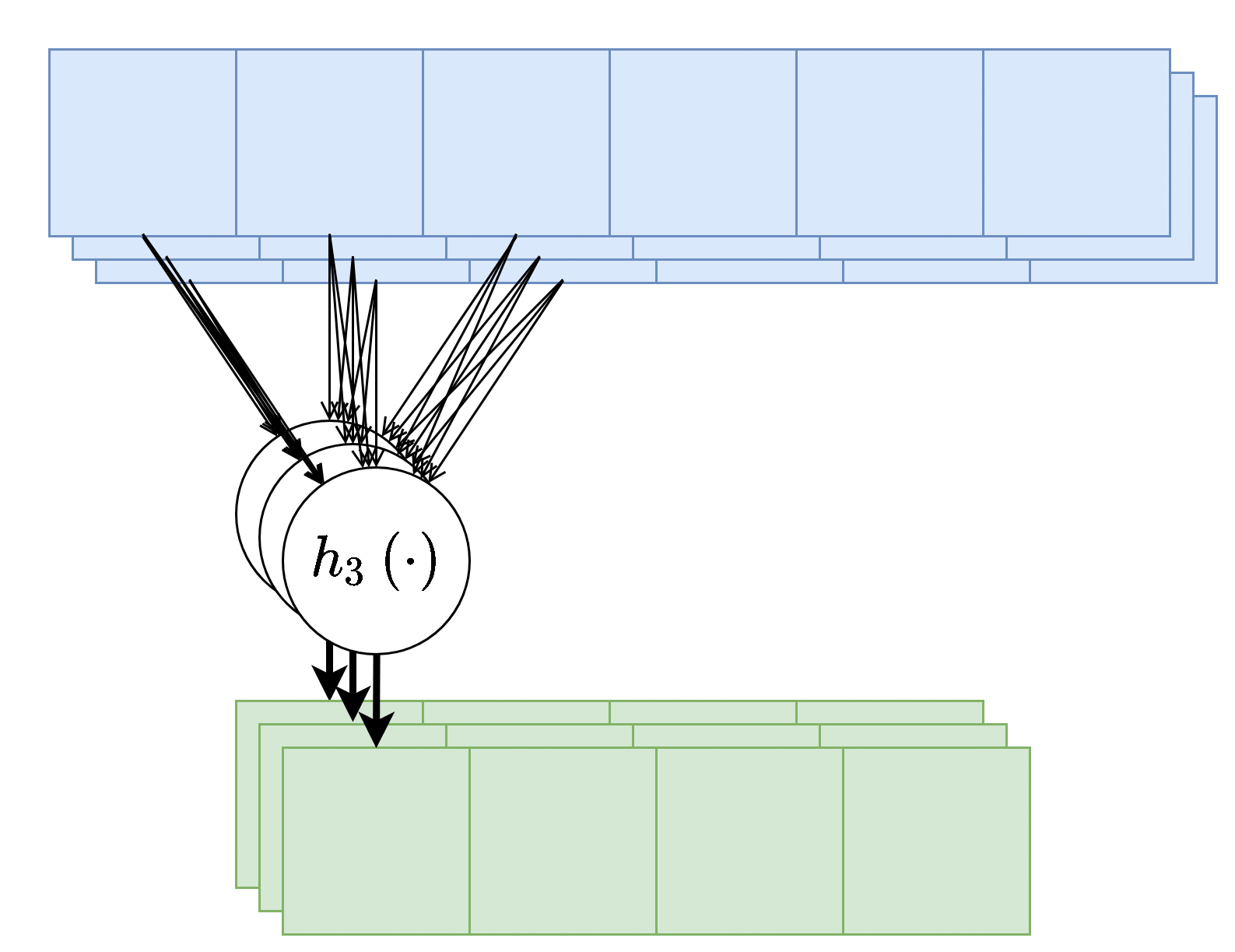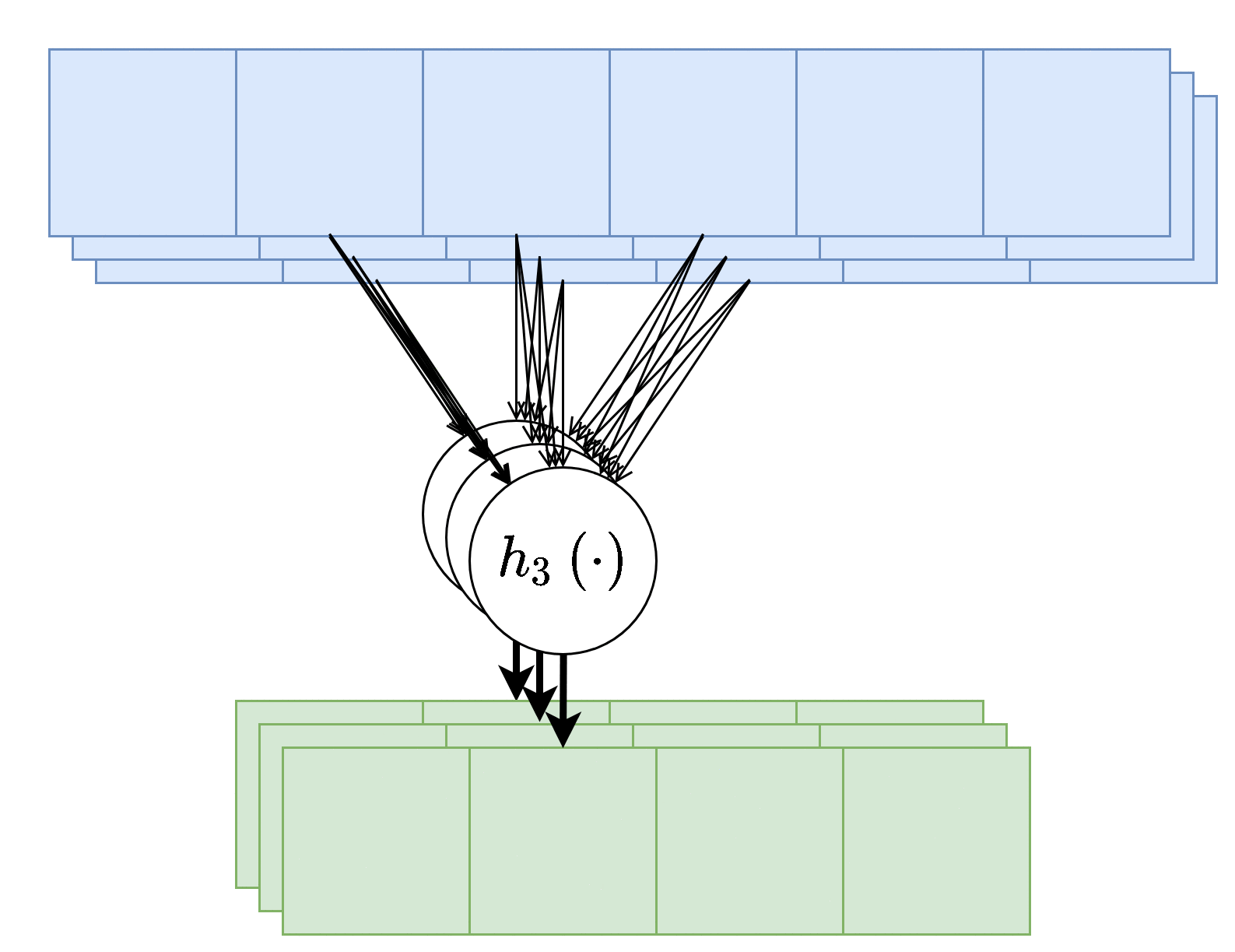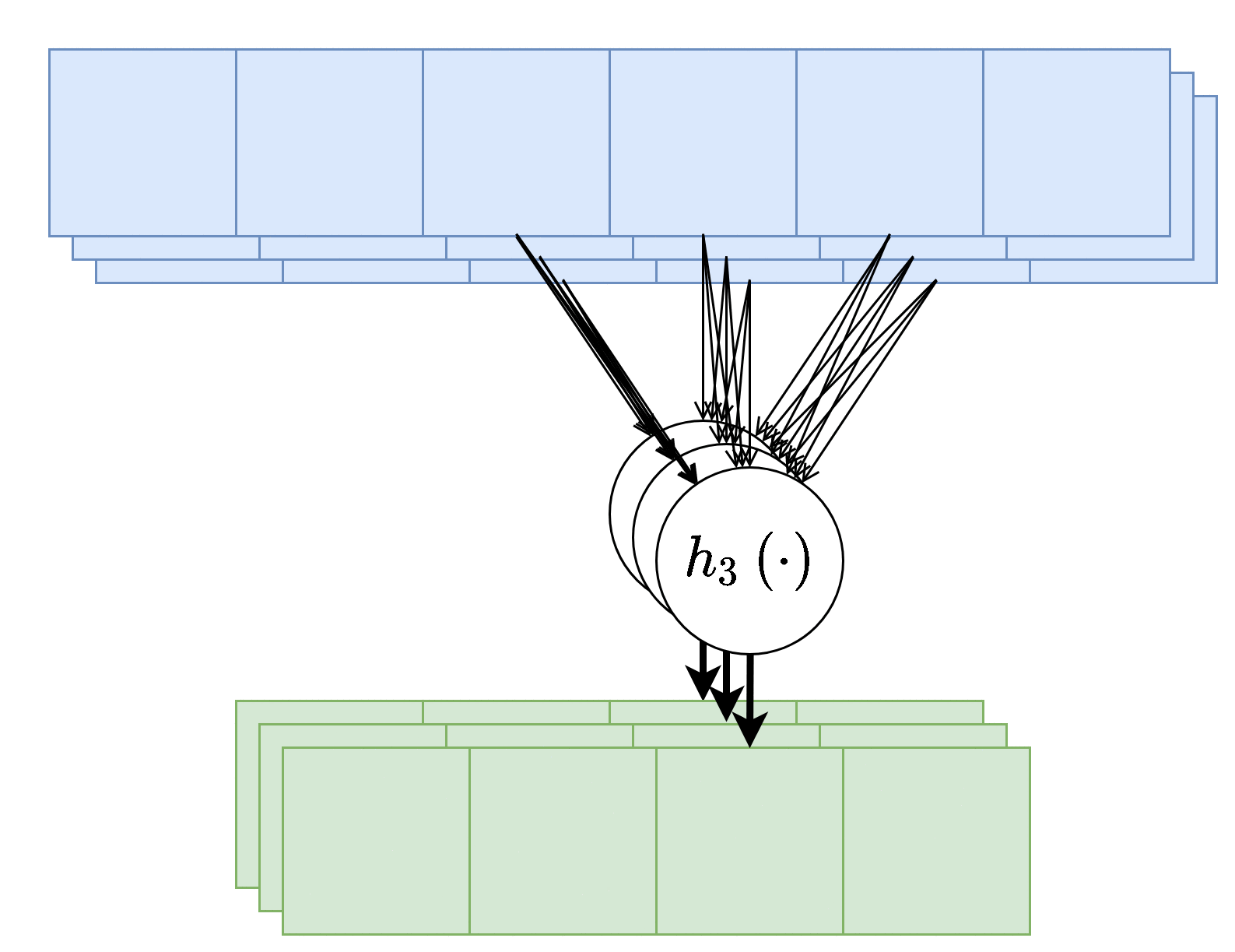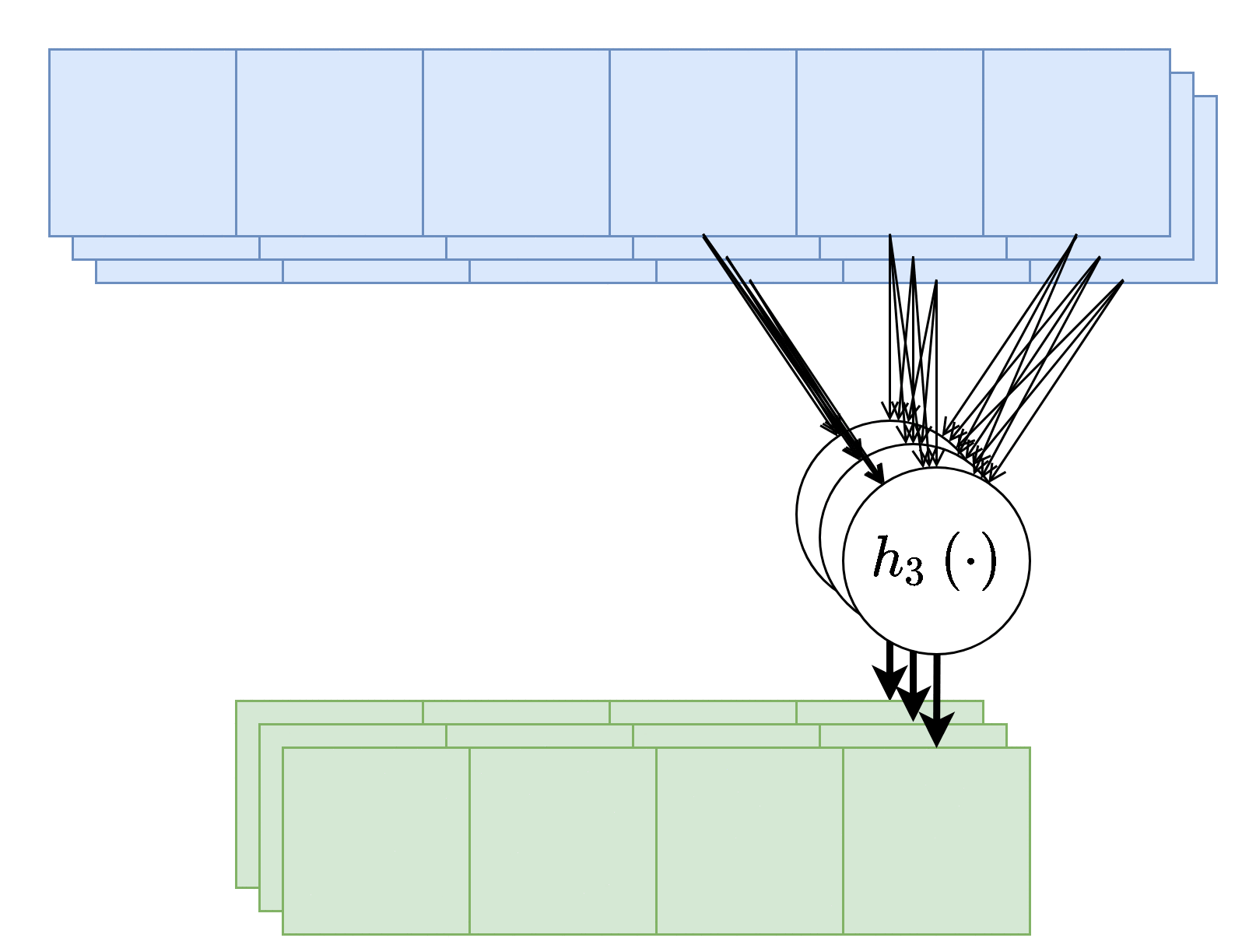
בשכבות אלו אין שיתוף של משקולות בין ערוצי הפלט השונים, כלומר כל גרעין קונבולציה הוא בעל סט משקולות יחודי הפועל על כל הערוצי הכניסה על מנת להוציא פלט יחיד. מספר הפרמטרים בשכבת כזאת היינו: $\underbrace{C_\text{in}\times C_\text{out}\times K}_\text{the weights}+\underbrace{C_\text{out}}_\text{the bias}$.

כאשר:

• $C_\text{in}$ - מספר ערוצי קלט.
• $C_\text{out}$ - מספר ערוצי פלט.
• $K$ - גודל הגרעין.

הרחבות נוספות של שכבות הקונבולוציה

לרוב מרחיבים מעט את ההגדרה של שכבת הקונבולוציה הבסיסית שהצגנו על ידי הוספת התכונות הבאות:

Padding - ריפוד

במידה ונרצה לשמור על הגודל הוקטור במוצא של שכבת הקונבולוציה, ניתן לרפד את וקטור הכניסה באפסים. לדוגמא:

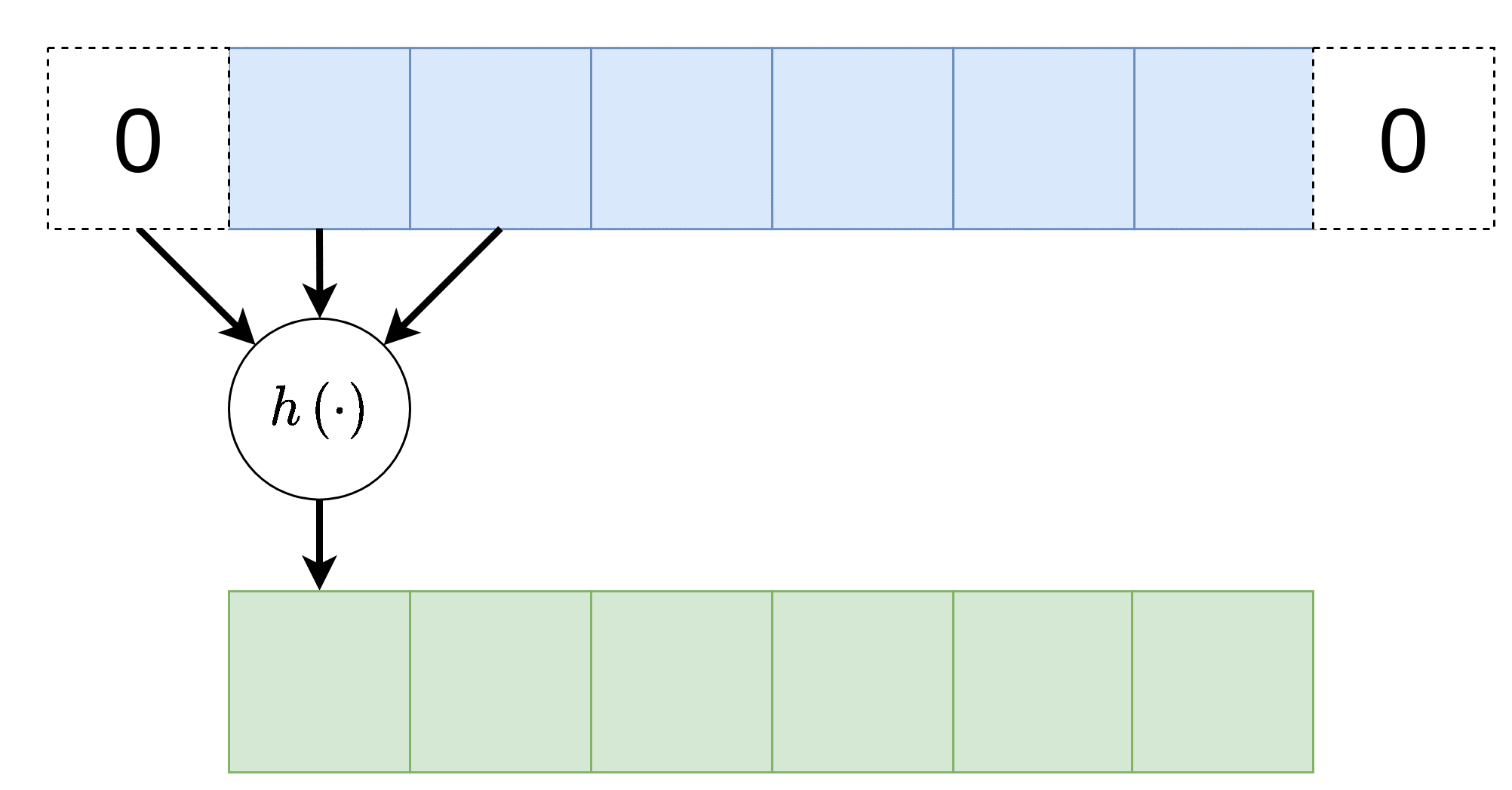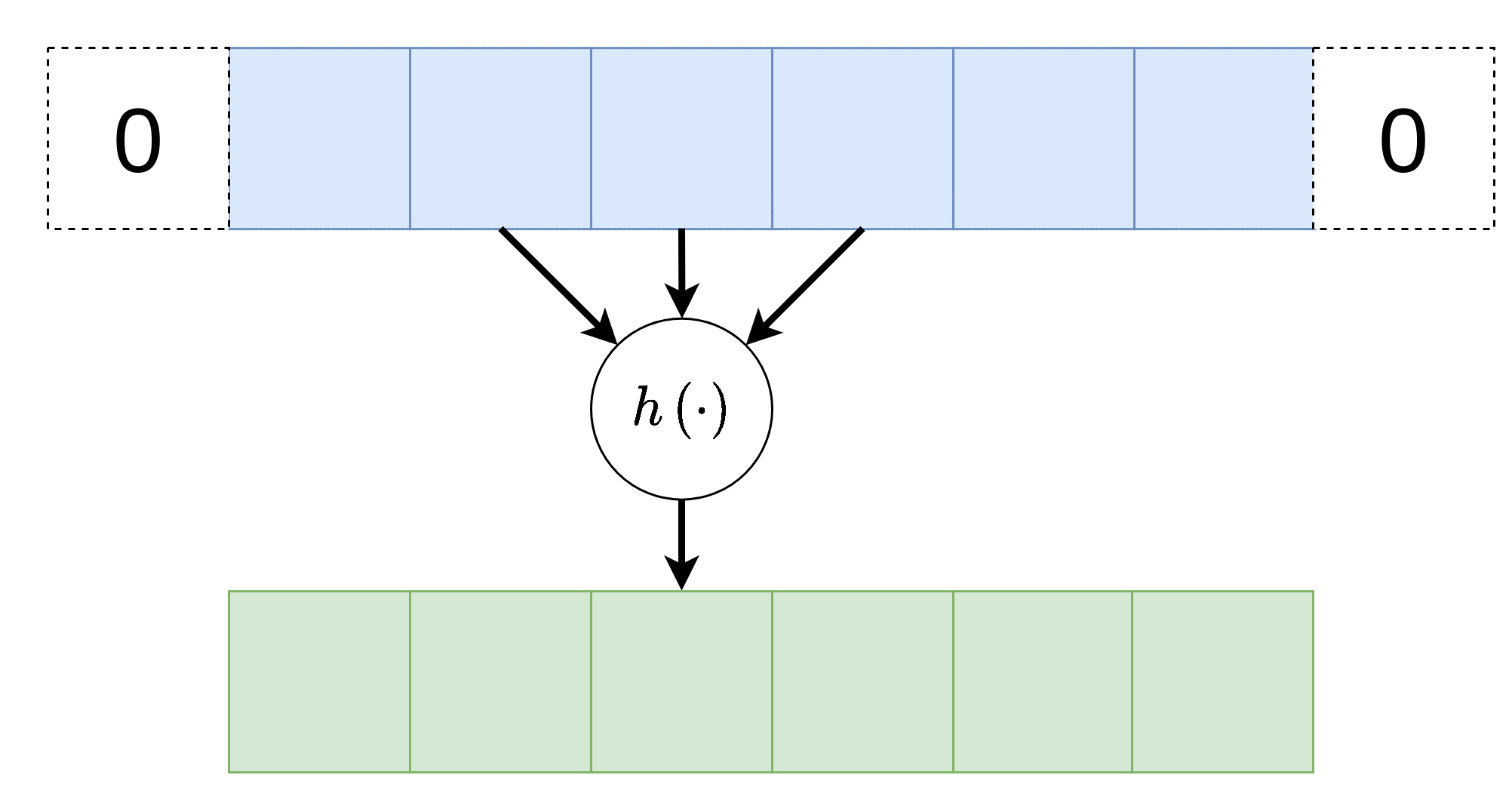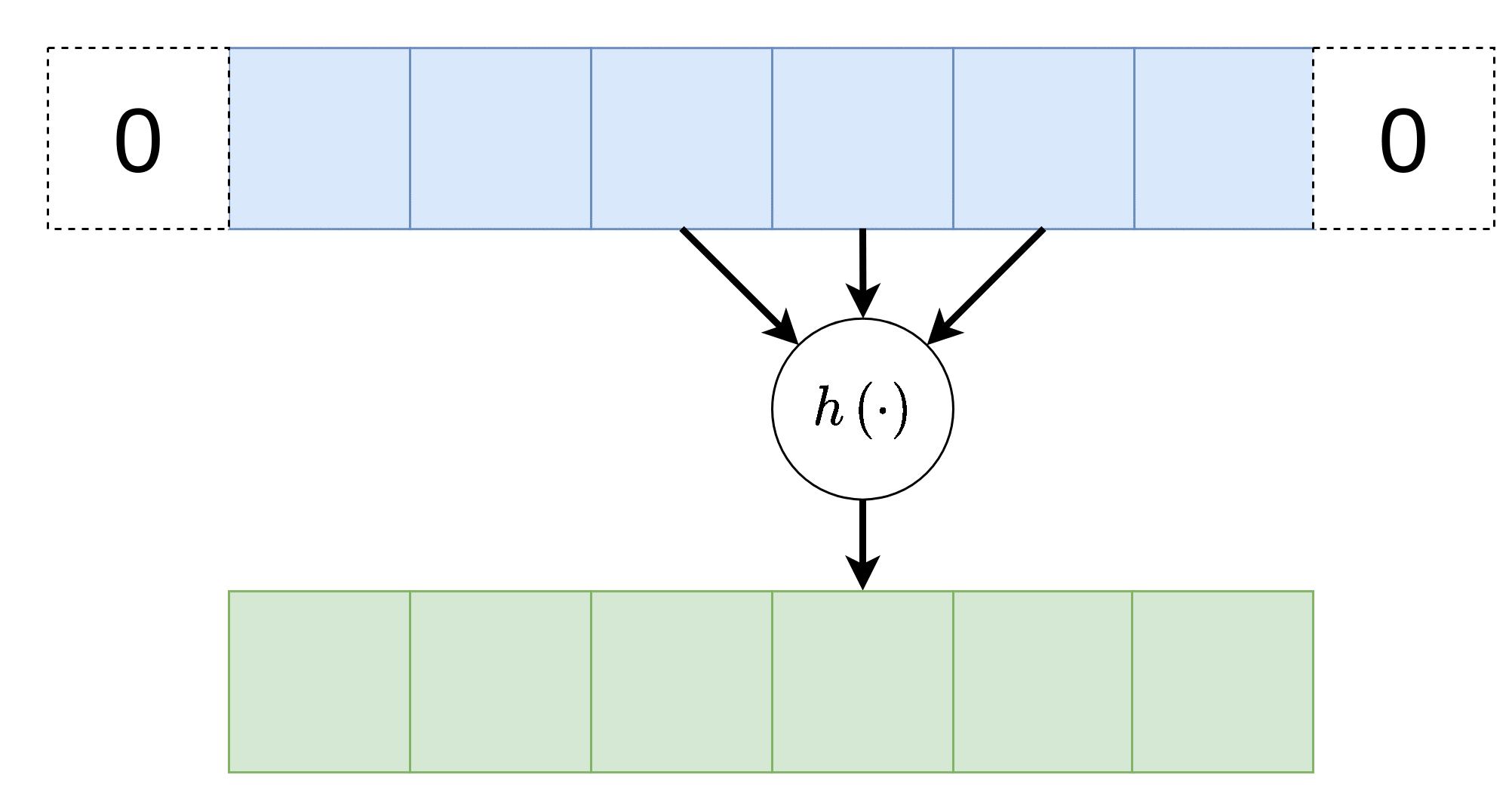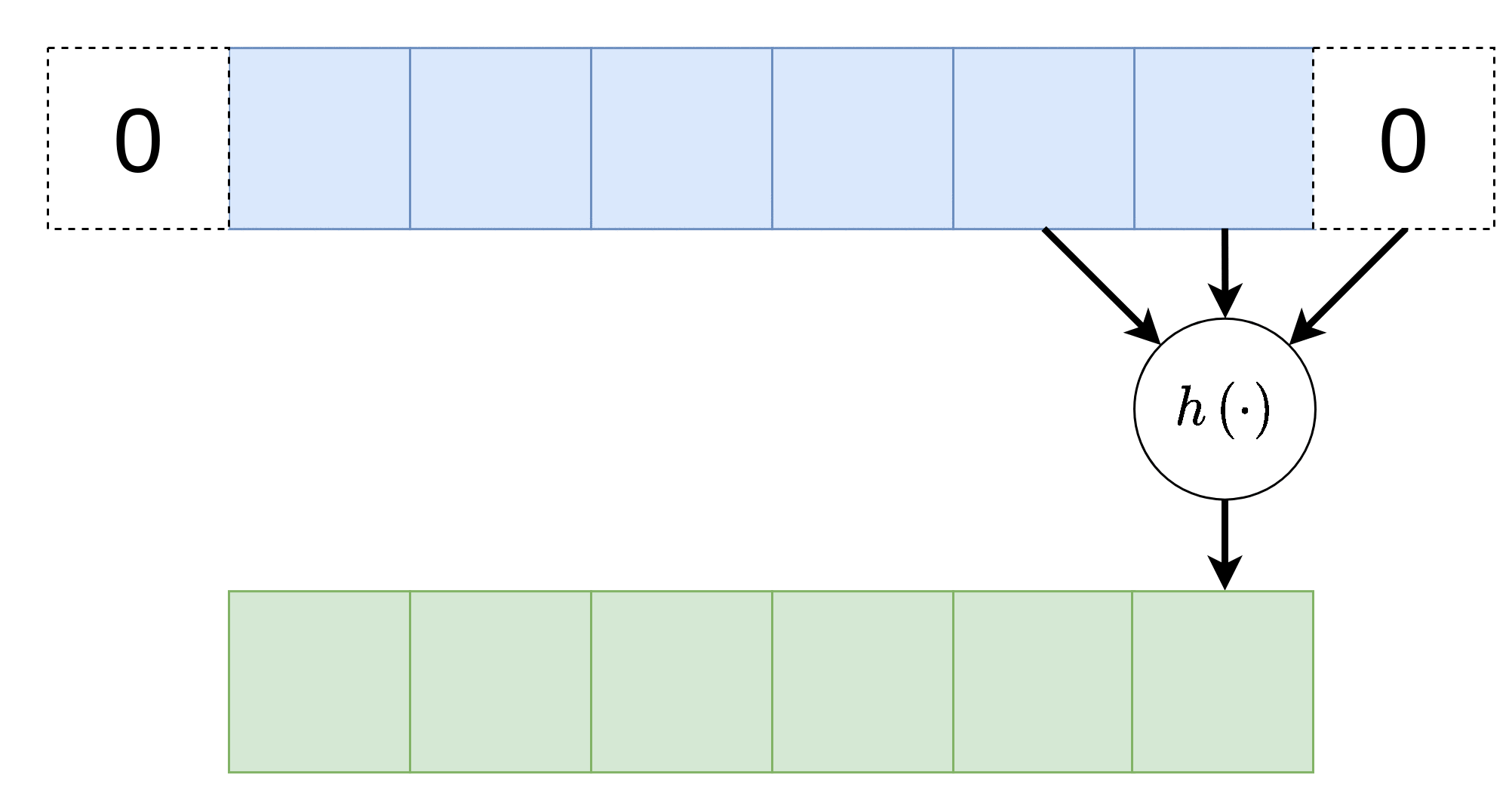
Stride - גודל צעד

לעיתים נרצה דווקא להקטין את גודל הוקטור במוצא בפקטור מסויים. דרך אחת לעשות זאת היא על ידי דילול המוצא. בפועל אין צורך לחשב את הערכים במוצא שנזרקים ולכן למעשה ניתן לחשב את הקונבולוציה בקפיצות מסויימות המכונות stride. אלא אם רשום אחרת, ה stride של שכבה הוא 1.

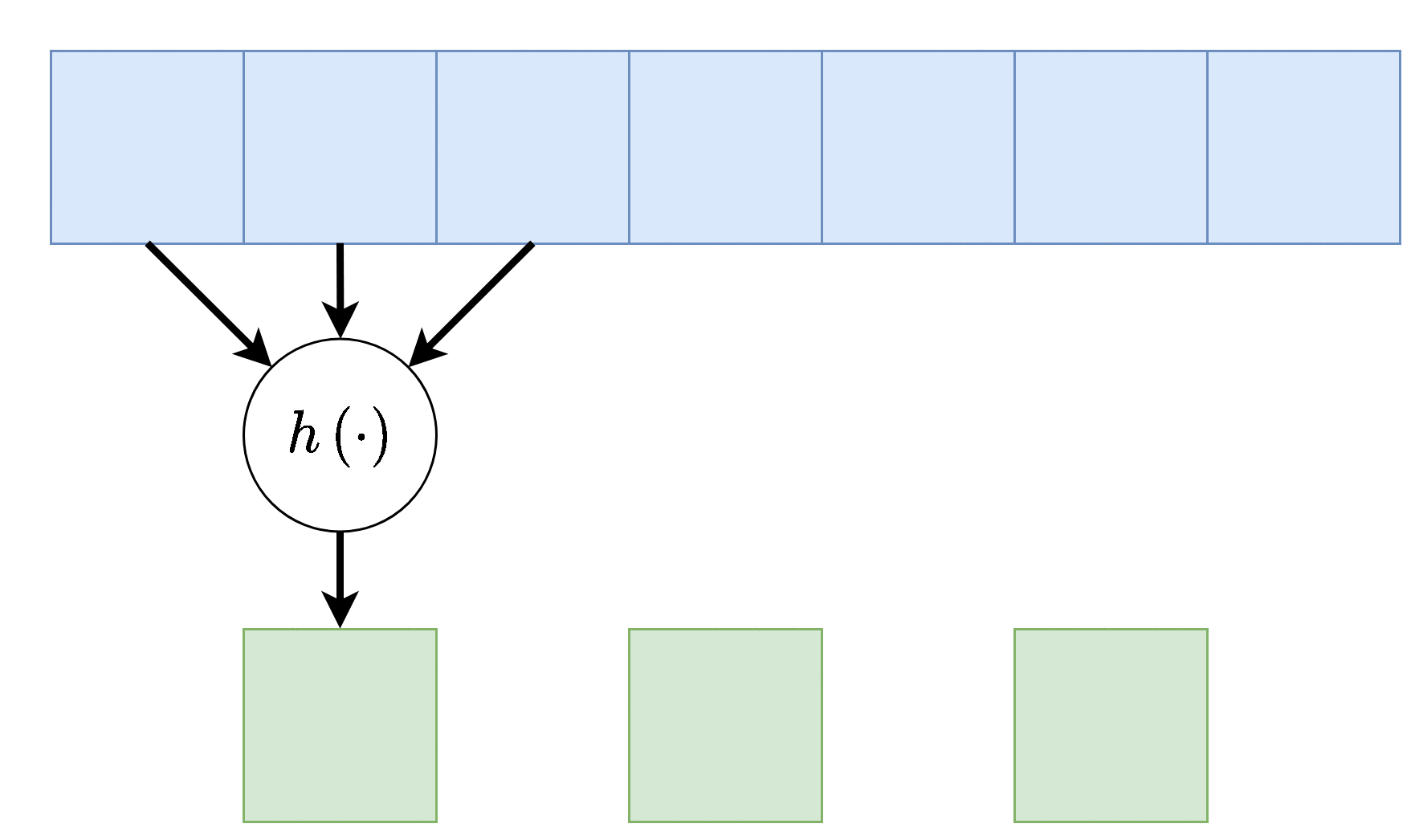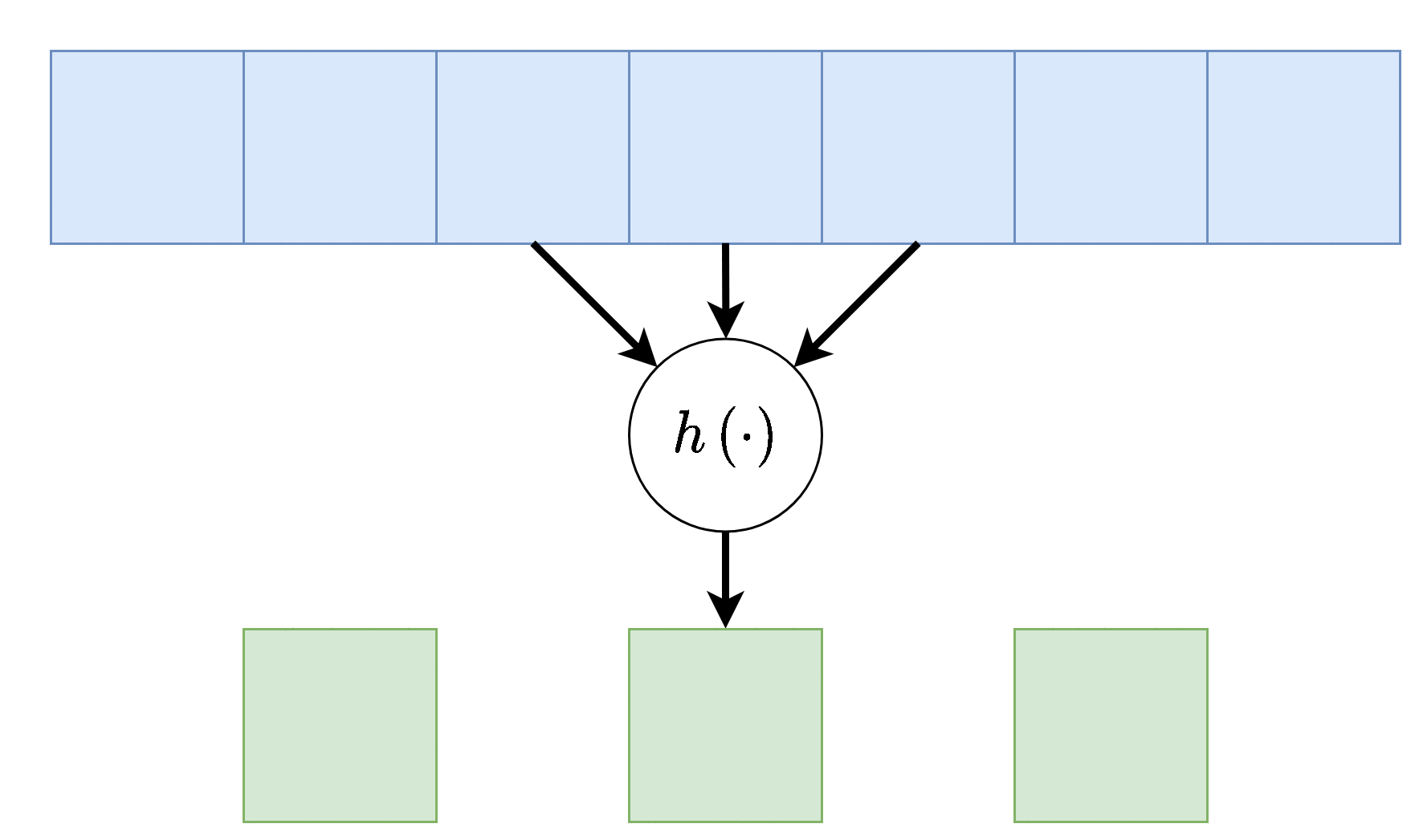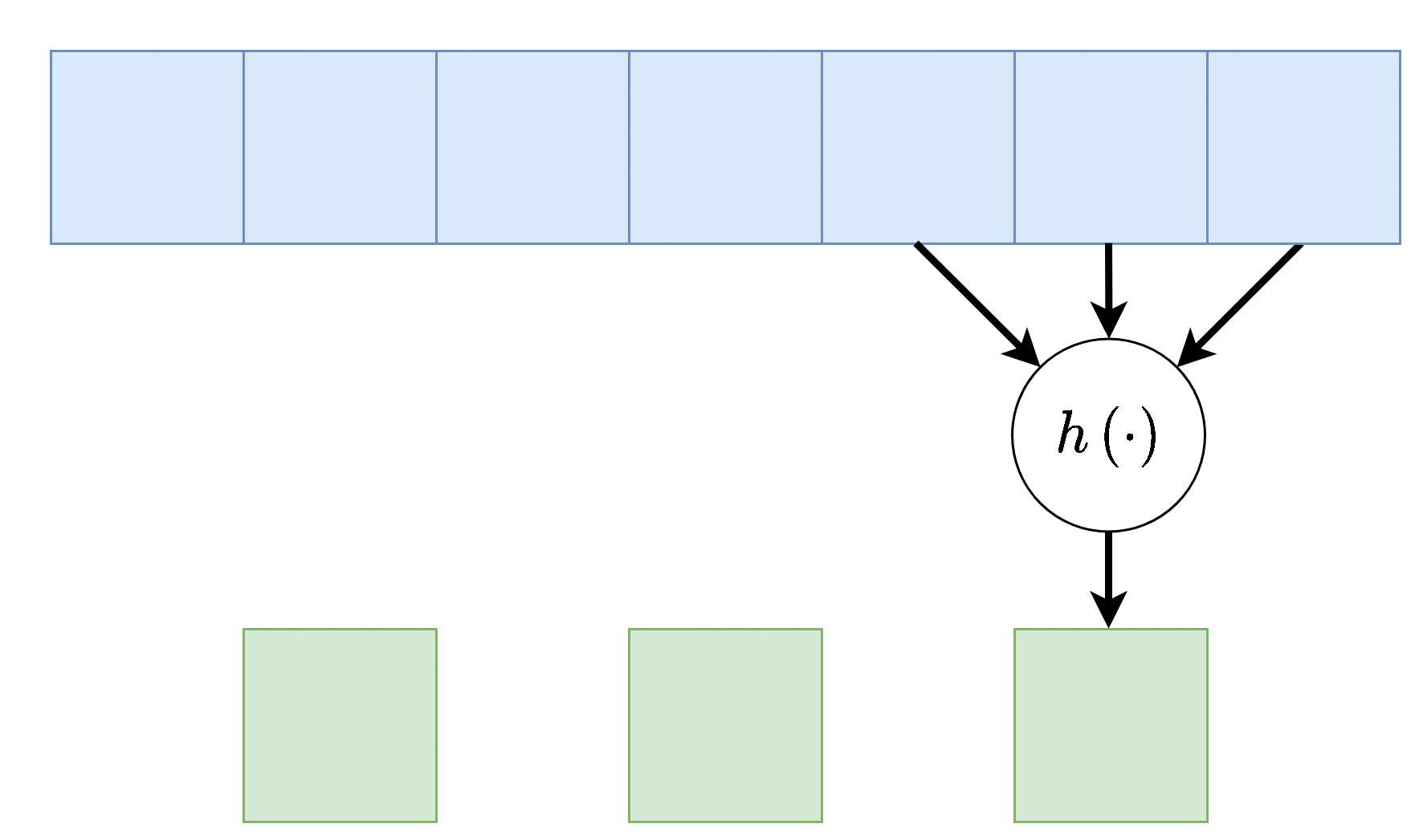
Dilation - התרחבות

במקרים אחרים נרצה לגדיל את האיזור שממנו אוסף נוירון מסויים את הקלט שלו מבלי להגדיל את מספר הפרמטרים ואת הסיבוכיות החישובית. לשם כך ניתן לדלל את הדרך בה נדגם הקלט על מנת להרחיב את איזור הקלט. אלא אם רשום אחרת, ה dilation של שכבה (הצפיפות בה הכניסה נדגמת) הוא 1.

Max / Average Pooling

שכבות נוספות אשר מופיעה במקרים רבים ברשתות CNN הן שכבות מסוג pooling. שכבות אלו מחליפות את פעולת הקונבולוציה בפונקציה קבועה אשר מייצרת סקלר מתוך מתוך הקלט של הנוירון. שתי שכבות pooling נפוצות הם max pooling ו average pooling, שכבה זו לוקחת את הממוצע או המקסימום של ערכי הכניסה.

דוגמא זו מציגה max pooling בגודל 2 עם גודל צעד (stride) גם כן של 2:

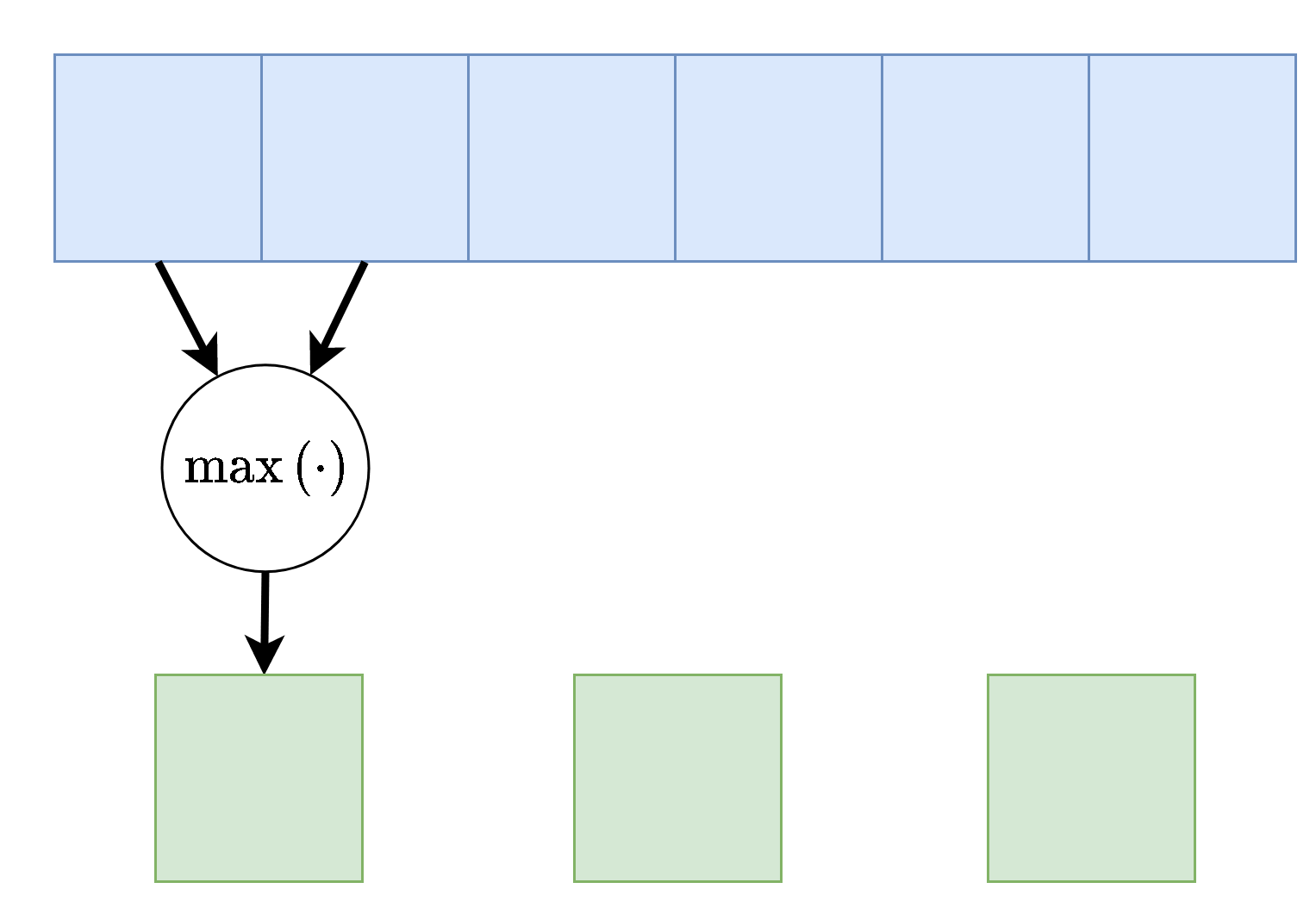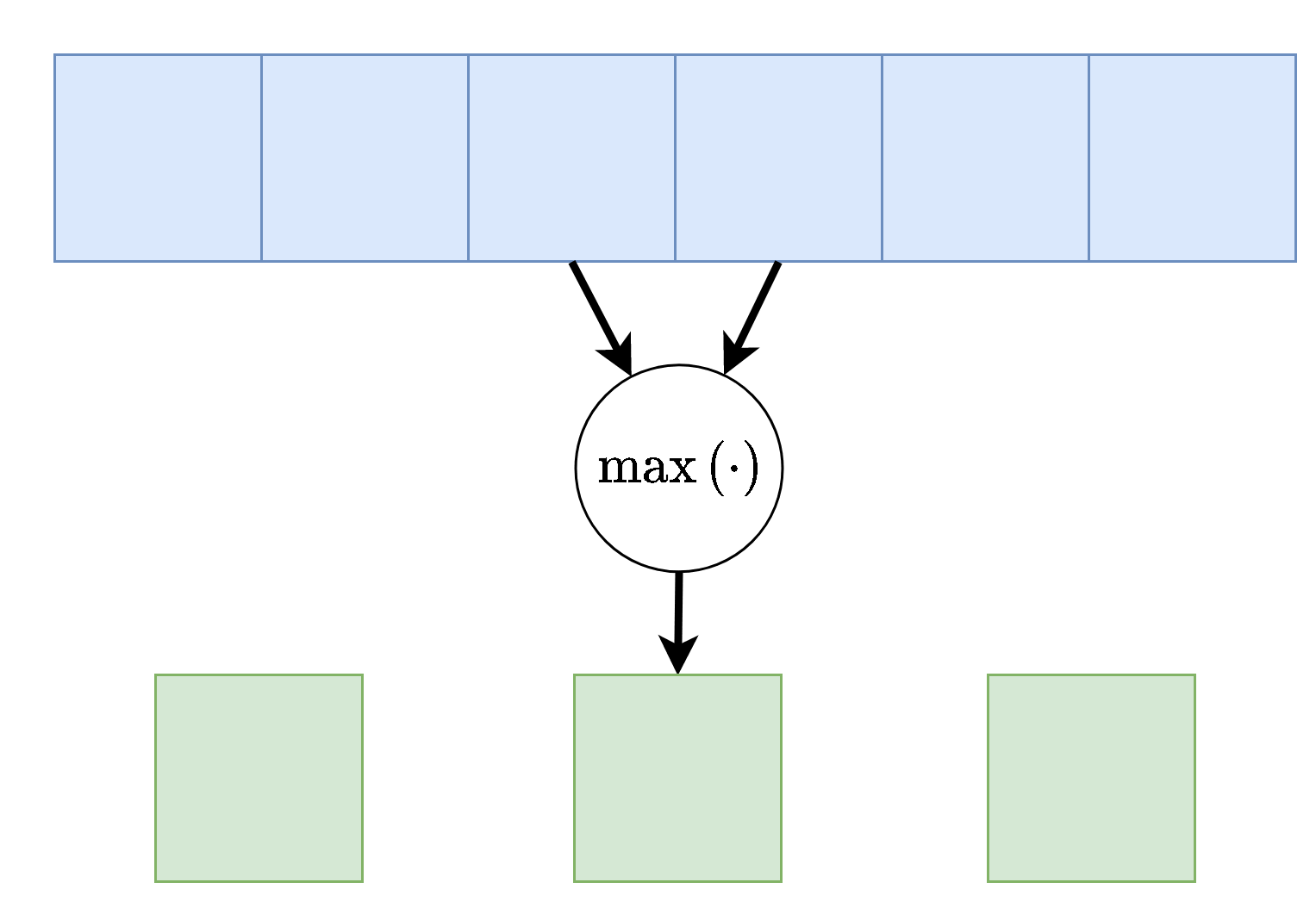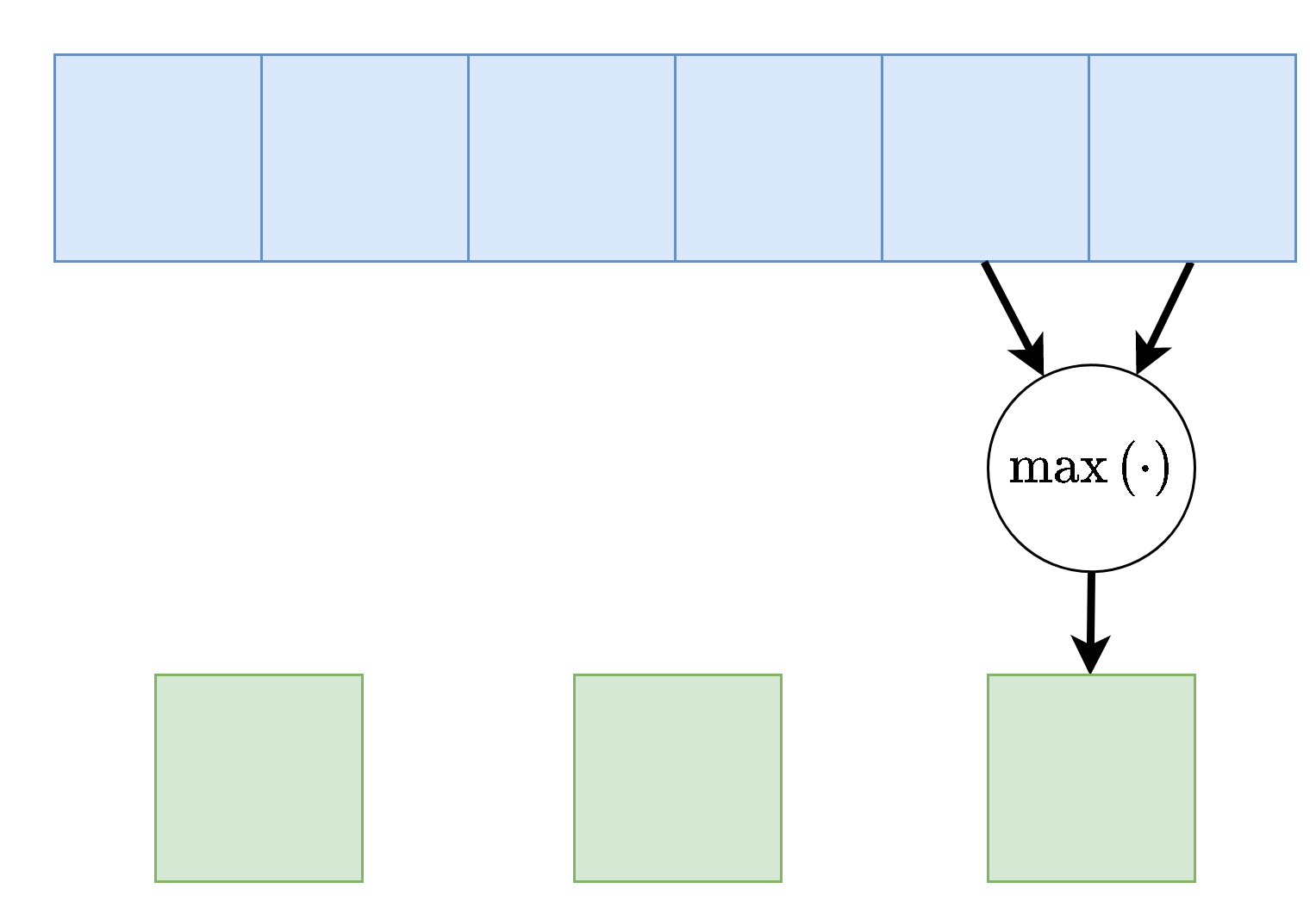
בשכבה זאת אין פרמטרים נלמדים.

2D Convolutional Layer

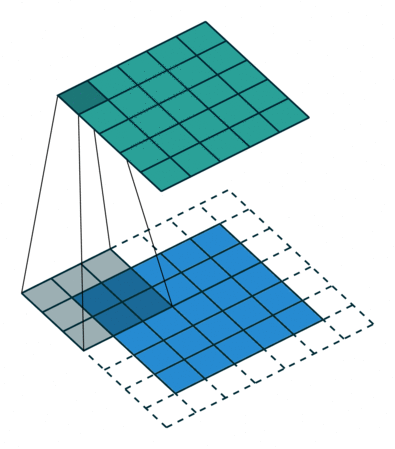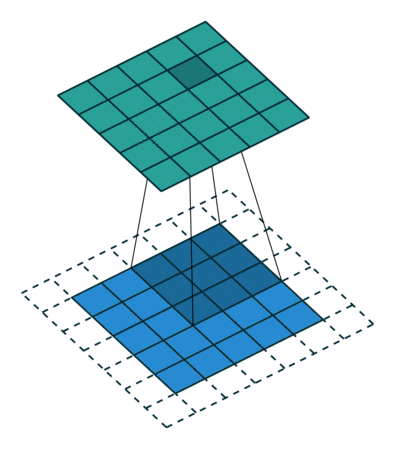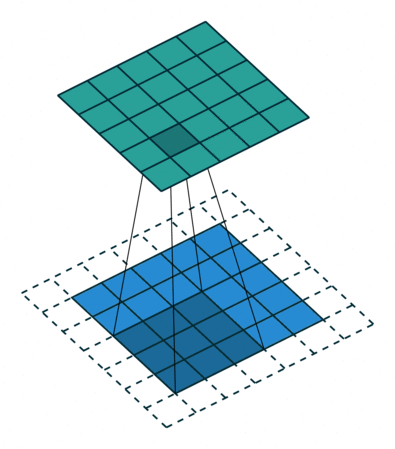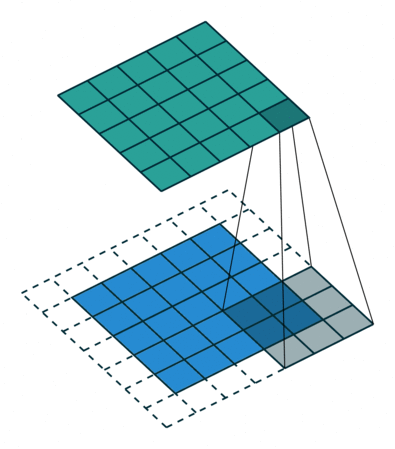
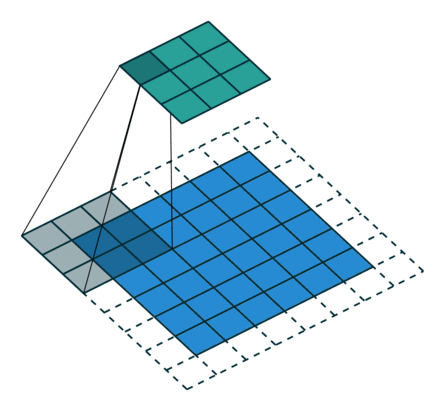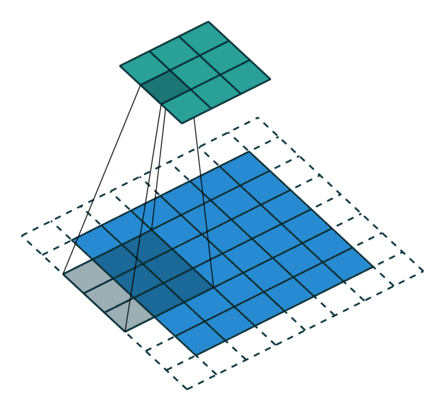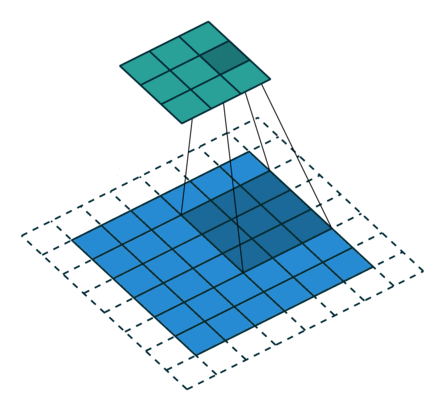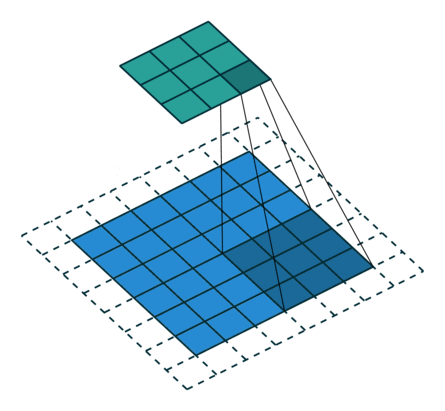
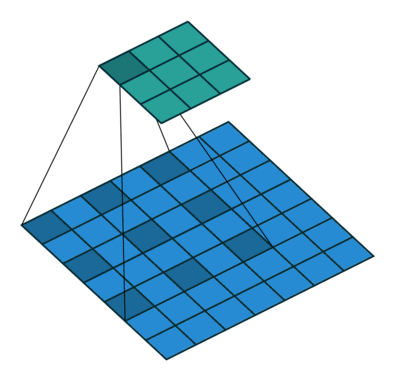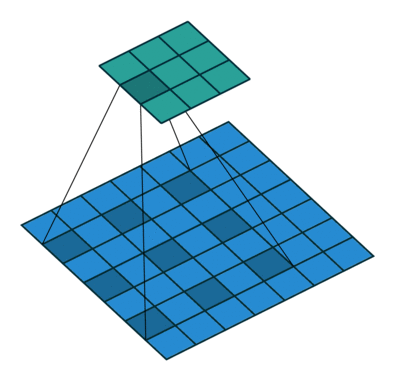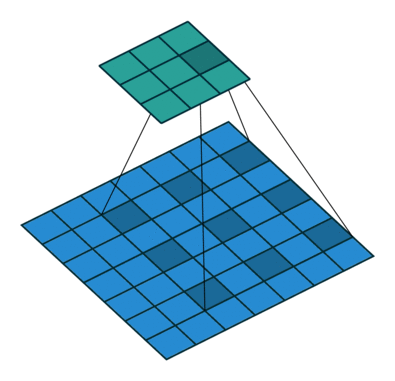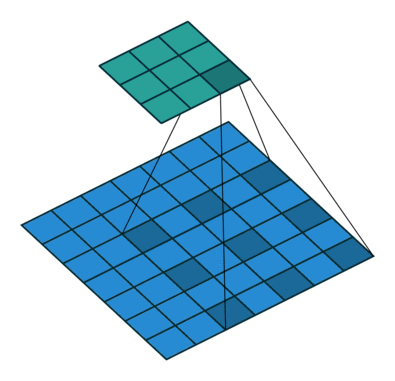
במרקים רבים נרצה לעבוד על קלט דו מימדי, לדוגמא על תמונות. במקרים כאלה הקונבולוציה תהיה דו מימדית. הגרפים הבאים מדגימים כיצד נראית פעולת שכבת הקונבולוציה על קלט דו מימדי (הירוק) אשר מייצרת פלט דו מימדי (הכחול) בעבור ערכים שונים של ה padding, stride ו dilation.

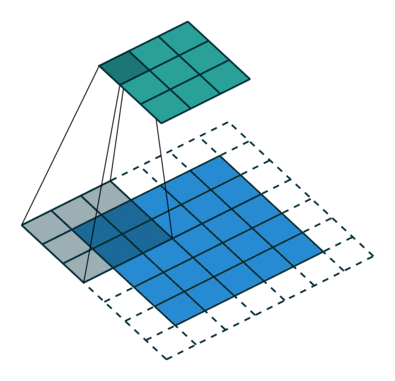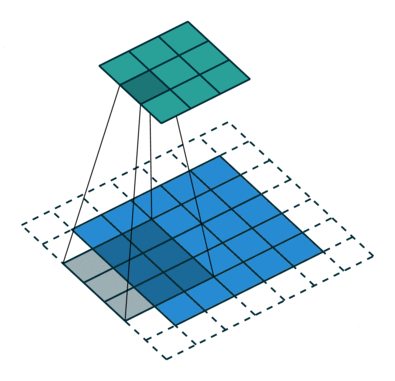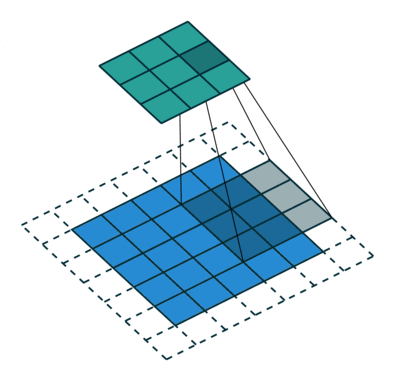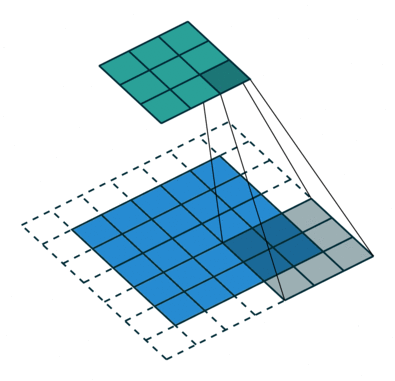
kernel size=3 padding=0 stride=1 dilation=1	kernel size=4 padding=2 stride=1 dilation=1	kernel size=3 padding=1 stride=1 dilation=1 (Half padding)	kernel size=3 padding=2 stride=1 dilation=1 (Full padding)
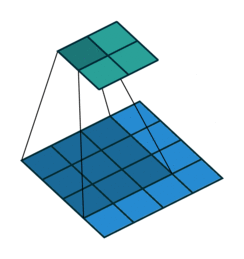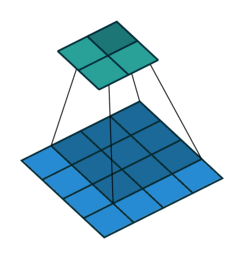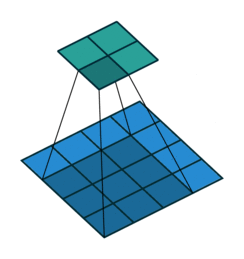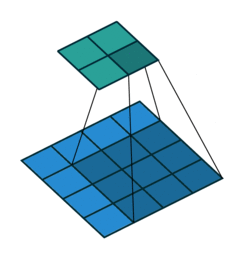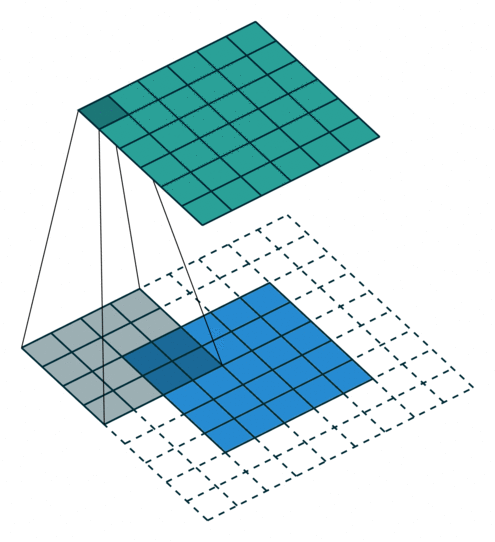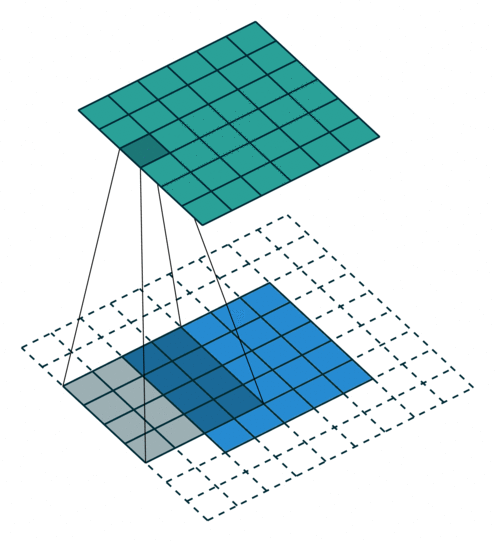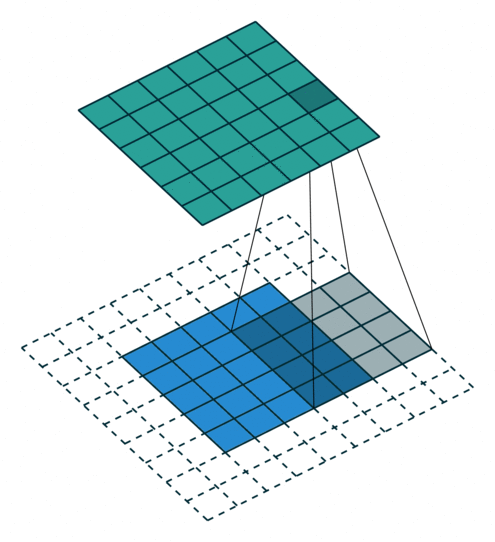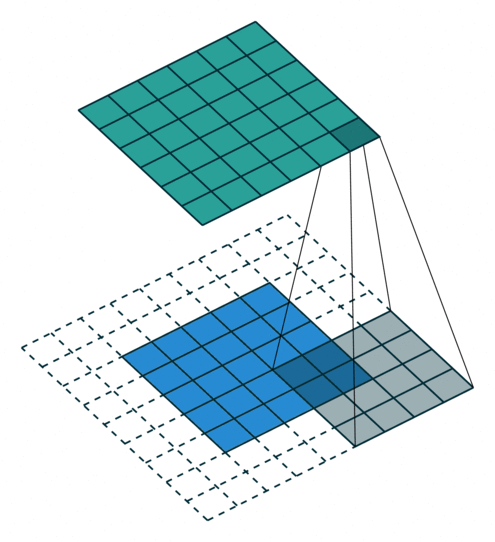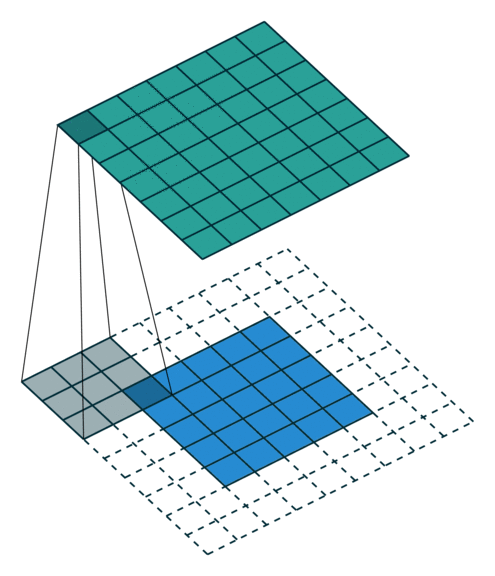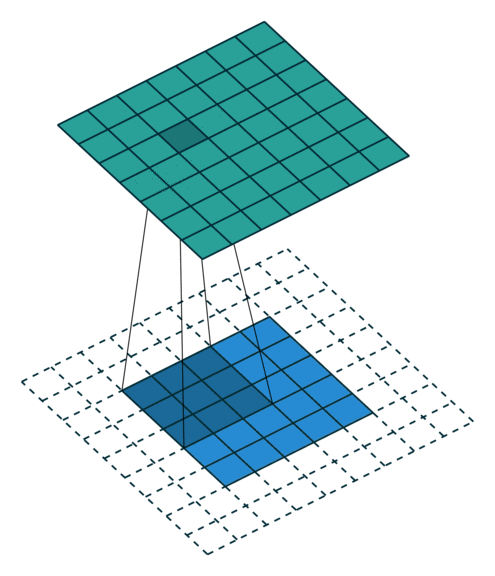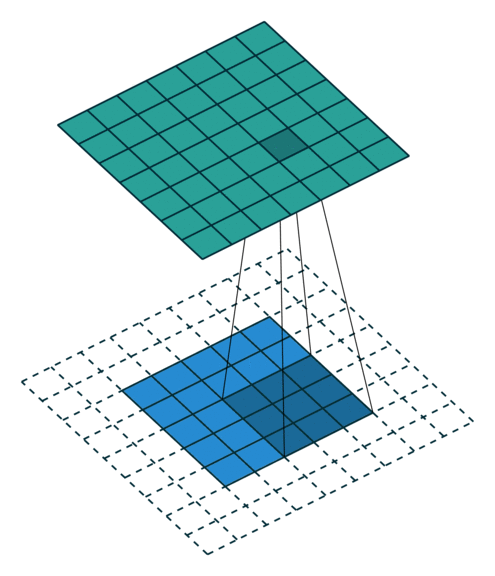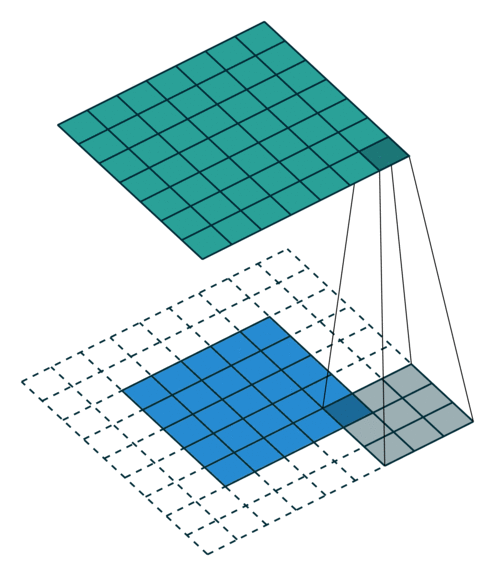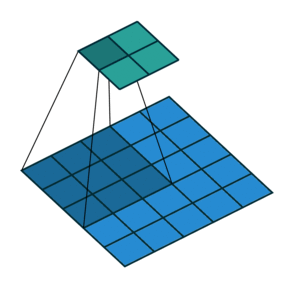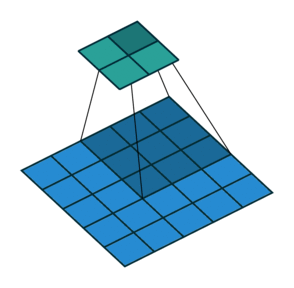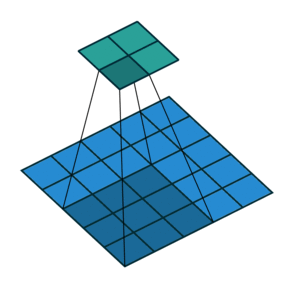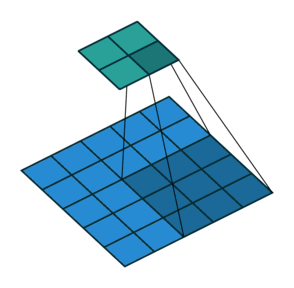
kernel size=3 padding=0 stride=2 dilation=1	kernel size=3 padding=1 stride=2 dilation=1	kernel size=3 padding=1 stride=2 dilation=1	kernel size=3 padding=0 stride=1 dilation=2

• [1] Vincent Dumoulin, Francesco Visin - A guide to convolution arithmetic for deep learning(BibTeX)

מבנה רשת CNN

רשתות קונבולוציה מורכבת משילוב של שכבות קנבולוציה, pooling ו FC. לדוגמא, אחת הרשתות הפופולריות היום לסיווג של תמונות הינה רשת בשם VGG-16. הרשת מקבלת תמונת צבע (3 ערוצים) בגודל 224x224 ומסווגת אותם ל 1 מ 1000 קטגוריות. הרשת נראית כך:

(כל שכבות הקונבולוציה ברשת הם בלי stride או dilation, זאת אומרת stride=1 ו dilation=1, ועם padding של 0 אחד בכל שפה על מנת לשמור על הגודל של התמונה בשכבות הקונבולוציה)

למה CNN כל כך טובים לבעיות מסויימות?

נסתכל על אחת הבעיות ש CNNs מאד טובים בלפתור, שהיא הבעיה של סיווג של תמונות לפי התוכן שלהם. הסיבה שבגללה CNNs מתאימים לפתרון של בעיה זו היא בין היתר בגלל שתי התכונות שמבדילות שכבת קנבולוציה משכבות FC ,שמתאימות לייצוג של הפתרון. נתייחס לכל אחת משתי התכונות בנפרד.

תלות של כל נוירון רק בסביבה המיידית שלו

התכונה הראשונה שמייחדת שכבות קונבולוציה הינה שכל נוירון מוזן מהערכים בסביבה המיידית שלו. תכונה זו מכריחה את הרשת לנסות לנתח את התמונה בצורה היררכית: ככל שמתקדמים בשכבות הנוירונים מסתכלים על איזורים הולכים וגדלים בתמונה ומנסים לזהות אובייקטים בגדלים שהולכים וגדלים. ניתן לראות זאת בשרטוט הבא:

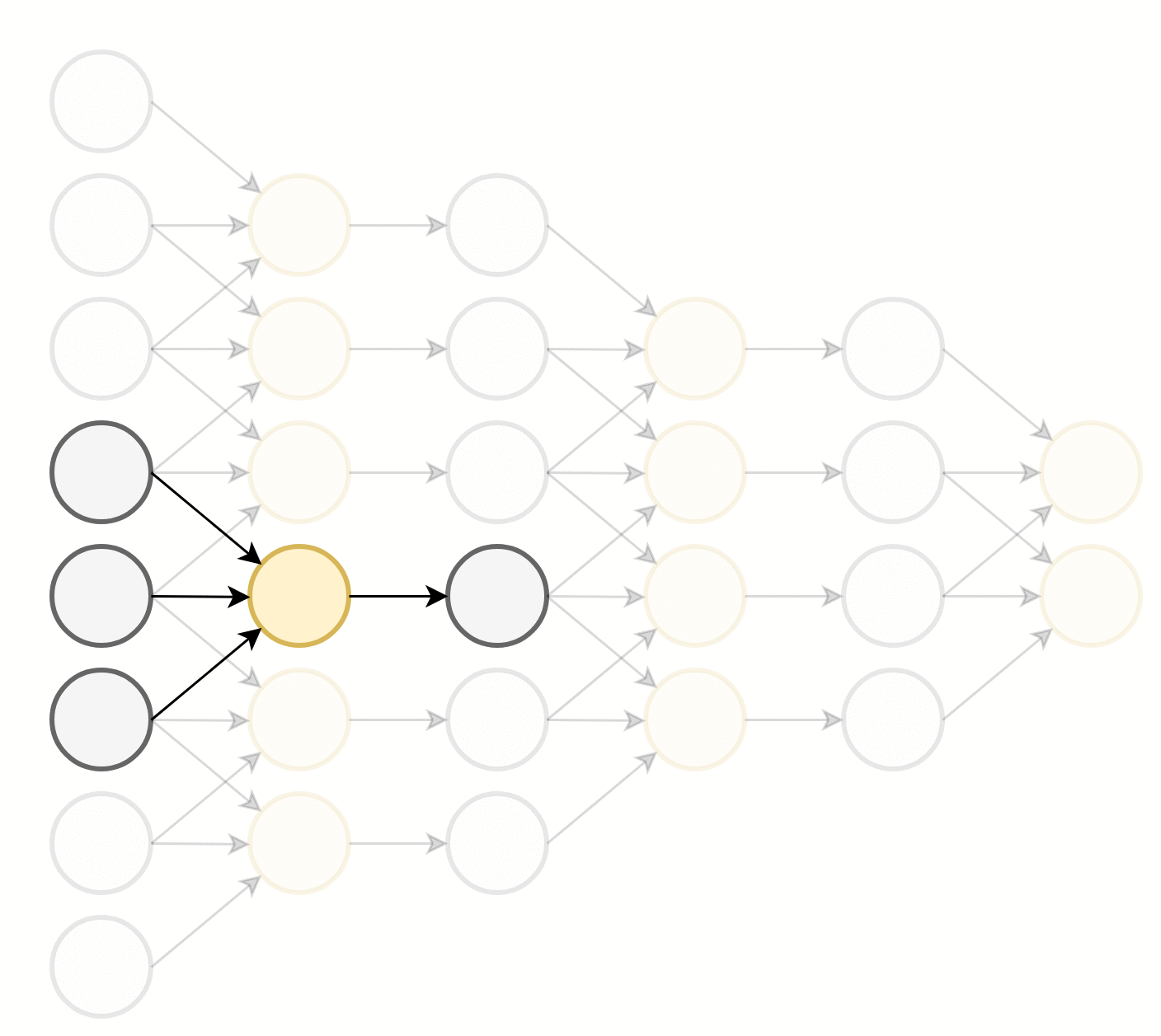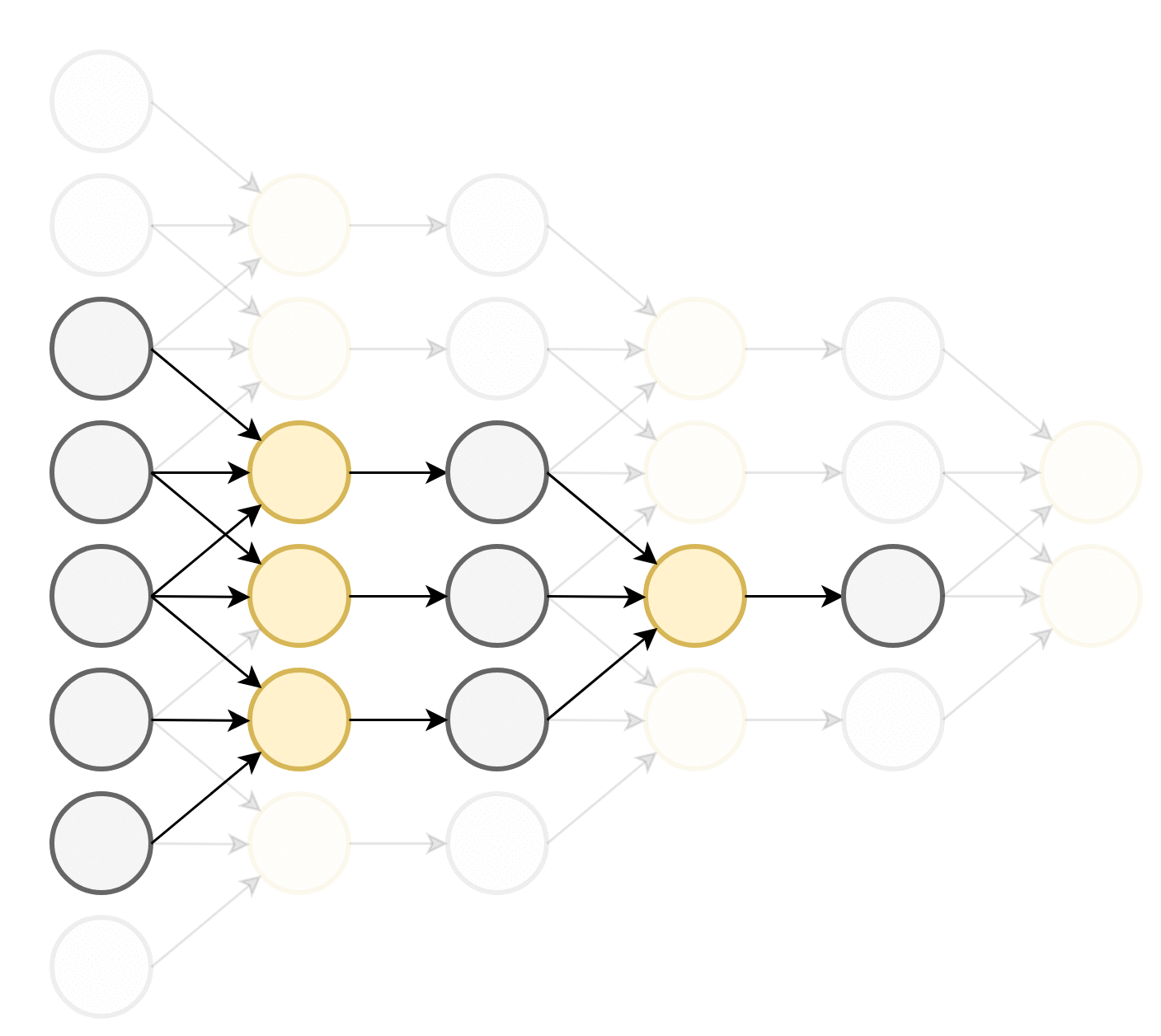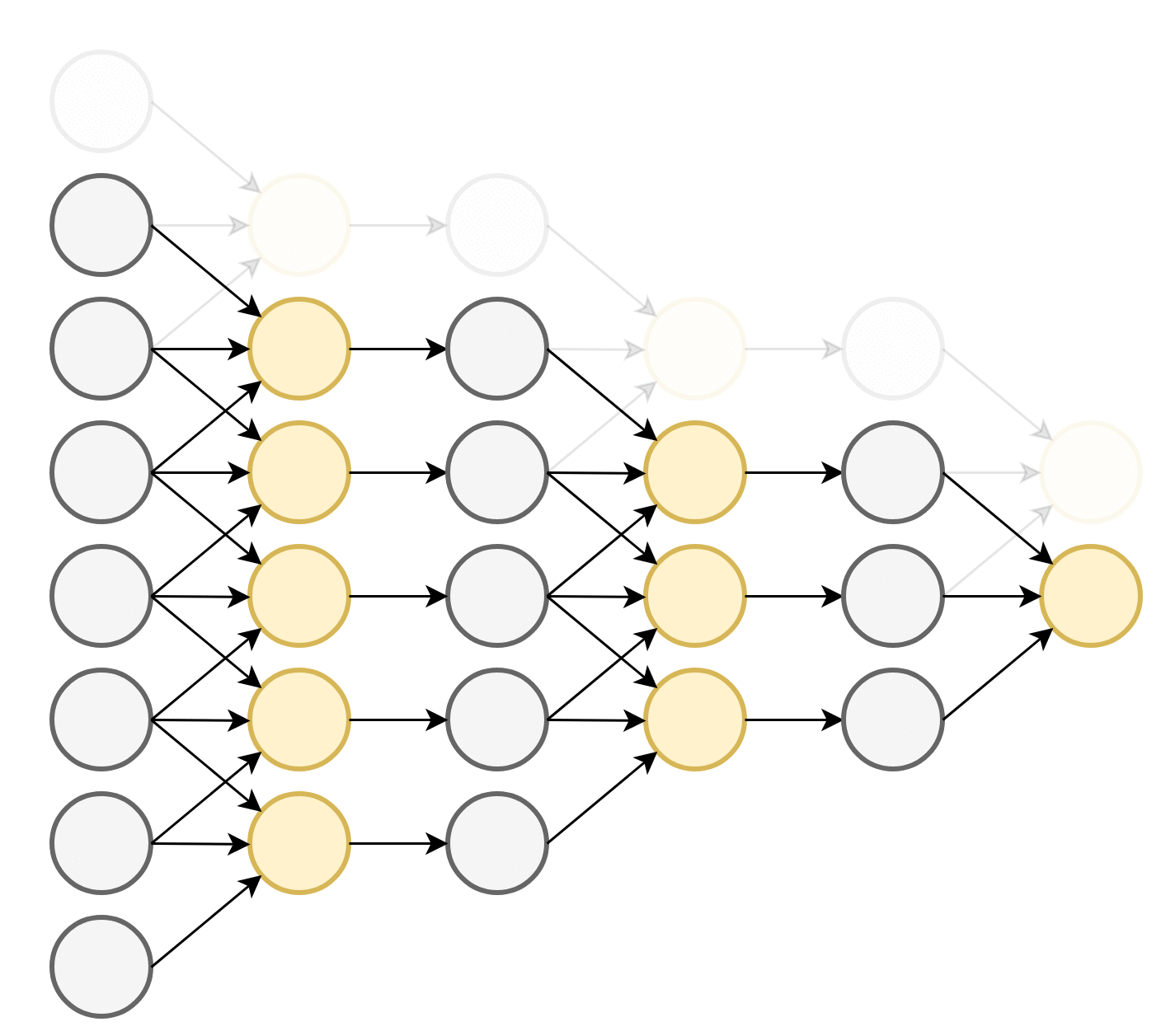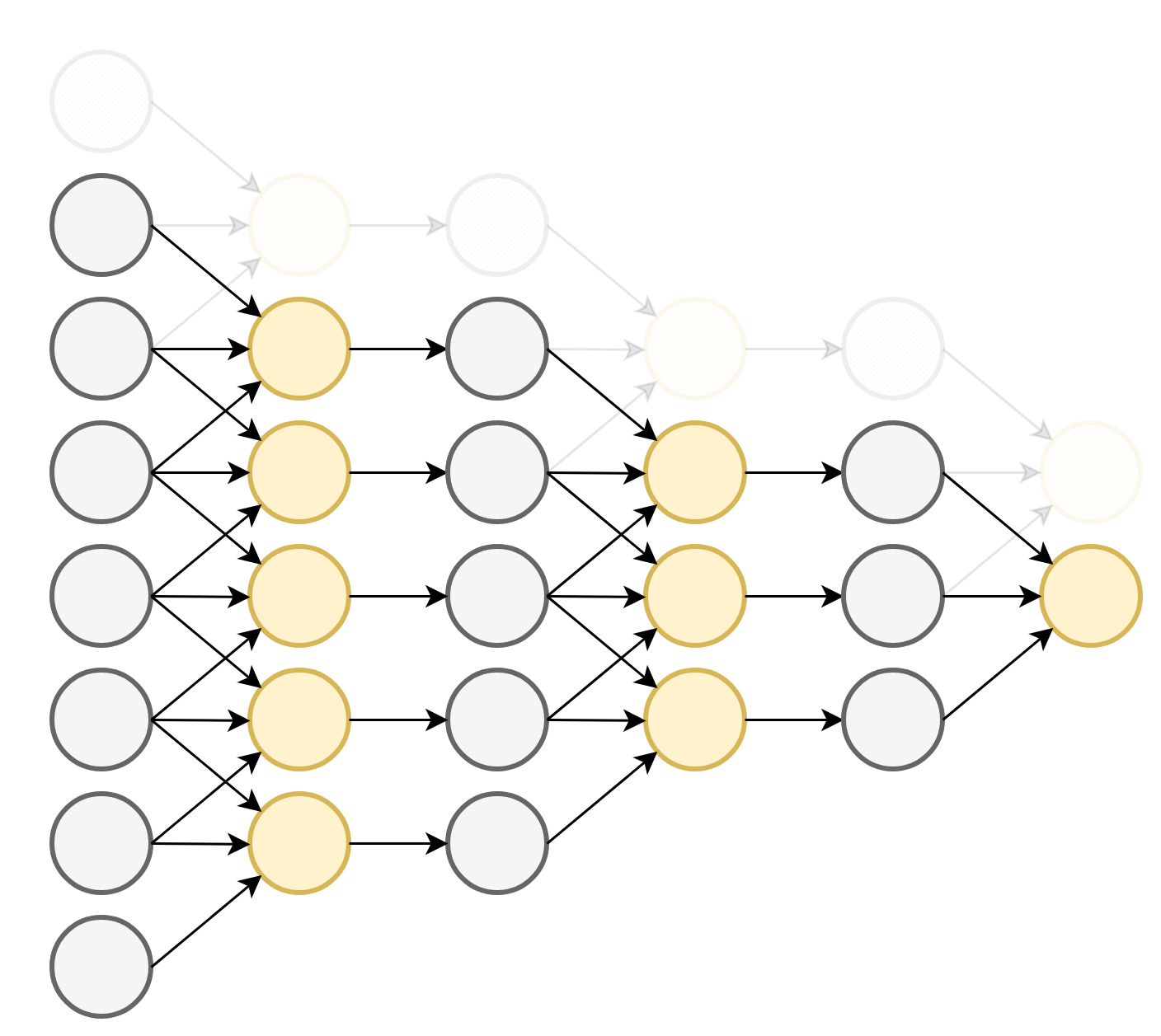
כל נוירון בשכבה הראשונה מושפע מאיזור באורך 3 בוקטור הכניסה. בשכבה השניה כל נוירון כבר יהיה מושפע מאיזור באורך 5 בוקטור הכניסה וכן הלאה. הגודל של האיזור שממנו מושפע נוירון בשכבה מסויימת נקרא ה receptive field שלו. לדוגמא, ה receptive field של נוירון בשכבה השלישית הוא 7.

בנוסף לשכבות הקונבולוציה שמגדילות את ה receptive field יש גם את שכבות ה pooling אשר מקטינות את המימדים ובכל מגדילות את ה reeptive filed של השכבות שאחריהם.

אם כן ברשתות אלו התפקיד של כל שכבה יהיה לנסות ולהבין מה המאפיינים של הסביבה שהם מושפעים ממנו על פי המאפיינים שהוציאה השכבה הקודמת.ש נדגים את הפעולה שמבצעת השכבה הראשונה ברשת אשר מנסה לזהות האם בתמונה מסויימת מופיע פרצוף.

גרעיני הקנובולוציה של השכבות הראשונות יעברו על התמונה ויחפשו, בעזרת קורלציה עם הגרעינים, תופעות בסיסיות כמו פסים אנכיים, פסים אופקיים, פינות, נקודות קטנות וכו'. כל גרעין ייצר ערוץ אשר מתאים לתופעה שאותה הוא מחפש. זאת אומרת שיהיה לנו ערוץ בעבור כל תופעה. לדוגמא הייצור של פסים אופקיים יעשה כך:

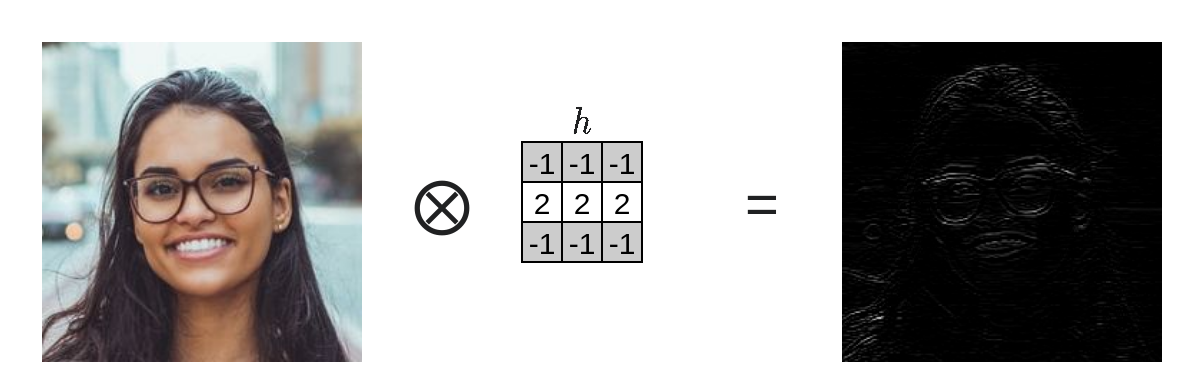
שכבת קונבולוציה עם 4 ערוצים במוצא תראה כך:

השכבות הבאות ברשת יחפשו אובייקטים אשר מורכבים מהתופעות שמצאו השכבות הראשונות. לדוגמא נוכל לחפש איזורים שמכילים הרבה פסים אנכיים בכדי לזהות איזורים שעשויים להכיל שיער, או לדוגמא לחפש שני פסים אופקיים סמוכים שעשויים להכיל שפתיים וכו'

מסתבר ששיטה זו, שבה הרשת מנסה להבין את תכולת התמונה באופן הירכי, היא מאד יעילה להבנת התמונה במספר יחסית קטן של פעולות, דבר שאר מסייע לרשתות CNN בפתרון של משימה זו.

Weight sharing

התכונה הנוספת של שכבת הקונבולוציה הינה שהמשקולות של כל הנוירונים משותפים בין כל הנוירונים באותה השכבה באותו ערוץ. ישנם מספר סיבות ללמה אילוץ זה לא מגביל מאד את היכולת לזהות אובייקטים:

1. הסיווג של התמונה לא אמור להיות מושפע אם מזיזים את האובייקט בתמונה מעט לצדדים. מהסיבה הזו אנו בעצם צריכים פונקציה שהיא בגדול איווריאנטית להזזות. בפועל זה אומר שאנו רוצים להפעיל את אותם הפעולות הלוקליות בשכבות הראשונות בצורה דומה בכל איזור בתמונה.
2. הפעולות שהשכבות הראשונות מבצעות, כגון חיפוש קווים אופקיים ואנכיים משותף לכל האובייקטים שנרצה לחפש בכל האיזורים בתמונה.

Batch Normalization (לא למבחן)

אחת הבעיות בעבודה עם רשתות עמוקות הינה שיכול להיווצר מצב שבו הערכים במוצא של כל שכבה הם מסדר גודל שונה. הדבר מאד משפיע על הגרדיאנטים של כל שיכבה ויכול ליצור גרדיאנטים בטווח ערכים מאד גדול שמאד מקשה על הבחירה של גודל הצעד. אנו נרחיב על כך בתרגול בהקשר של האיתחול של הפרמטרים של הרשת באלגוריתם ה gradient descent.

דרך אחת לנסות ולהבטיח כי המוצאים של כל שכבה יהיו בערך מאותו סדר גודל הינה על ידי הוספה של שכבה בשם batch normalization אשר מנסה לנרמל את הערכים אשר עוברים דרכה (מביאה את התוחלת של הערכים ל 0 ואת הסטיית תקן ל 1). הדרך שהיא עושה זאת הינה על ידי חישוב התוחלת וסטיית התקן האמפירית של הערכים על פני ה batch הספציפי באותו צעד גרדיאנט.

נסתכל על שכבת batch norm המקבלת וקטור $\boldsymbol{z}_{\text{in}}$ ומוציאה וקטור $\boldsymbol{z}_{\text{out}}$:

נניח כי בצעד עדכון מסויים אנו רוצים לחשב את הגרדיאנט של הרשת בעבור mini-batch מסויים $\{\boldsymbol{x}^{(i)}\}_{i=1}^M$. נניח כי הוקטורים המתקבלים בכניסה לשכבת ה batch norm הם $\{\boldsymbol{z}_{\text{in}}^{(i)}\}_{i=1}^M$. שיכבת ה batch norm תחשב את התוחלת וסטיית התקן האמפירית של הכניסה באופן הבא:

$$\boldsymbol{\mu}=\frac{1}{M}\sum_{i=1}^M \boldsymbol{z}_{\text{in}}^{(i)}$$ $$\sigma^2=\frac{1}{M}\sum_{i=1}^M (\boldsymbol{z}_{\text{in}}^{(i)}-\boldsymbol{\mu})^2$$

המוצא של השכבה יהיה:

$$\boldsymbol{z}_{\text{out}}=\frac{ \boldsymbol{z}_{\text{in}}-\boldsymbol{\mu} }{\sigma+\epsilon}$$

כאשר $\epsilon$ הוא מספר קטן כל שהוא אשר אמור למנוע חלוקה ב 0.

לרוב השכבה תכיל גם טרנספורמציה לינארית נלמדת עם פרמטרים $\gamma$ ו $\beta$:

$$\boldsymbol{z}_{\text{out}}=\frac{ \boldsymbol{z}_{\text{in}}-\boldsymbol{\mu} }{\sigma+\epsilon}\cdot\gamma+\beta$$

כאשר $\gamma$ ו $\beta$ הוא וקטורים באורך של $\boldsymbol{z}$ והמכפלה עם $\gamma$ היא איבר איבר.

אחרי שלב האימון

במהלך הלימוד מחזיקים ממוצע נע (exponantial moving average) של הערכים $\mu$ ו $\sigma$ ובסוף שלב הלימוד מקבעים את הערכים שלהם ואלו הערכים שבהם הרשת תשתמש לאחר שלב האימון.