הרצאה 10 - Neural Networks

מה נלמד היום

רשת נוירונים מלאכותית כמודל פרמטרי

במקומות רבים בתחום של מערכות לומדות נרצה למצוא פונקציה שתבצע פעולה מסויימת או תתאר תופעה מסויימת. בקורס זה ניסינו למצוא פונקציות שיבצעו פעולות חיזוי או שיתארו פילוגים של משתנים אקראיים, כמו כן ראינו כי דרך נוחה לעשות זאת היא על ידי שימוש במודל פרמטרי ומציאת הפרמטרים האופטימאלייים של המודל.

עד כה בעיקר עבדנו עם מודלים שהם לינאריים בפרמטרים של המודל. באופן תיאורטי יכול הייצוג של מודלים שכאלה היא בלתי מוגבלת שכן אנו יודעים לדוגמא נוכל לקרב הרבה מאד פונקציות עם פולינום מסדר מספיק גבוהה. הבעיה היא שבמרבית המקרים העבודה עם פולינומים מסדרים גבוהים היא לא מאד פרקטית. אחת הבעיות של פולינומים היא העובדה שכמות הפרמטרית היא מסדר גודל של האורך של וקטור הכניסה $\boldsymbol{x}$ בחזקת סדר הפולינום: $D^k$, כאשר $D$ הוא מאד גדול כמות הפרמטרים גדלה בקצב מאד מהיר עם סדר הפולינום. לדוגמא, בעבור תמונה יחסית קטנה של 100x100 פיקסלים למודל פרמטרי שהוא פולינום מסדר שלישי יהיו טריליון פרמטרים, שזה מספר לא ריאלי.

נשאלת אם כן השאלה האם ישנם מודלים מתאימים יותר.

נוירון ביולוגי

בשנים האחרונות מודלים פרמטריים המכונים רשתות נוירונים מלאכותיות (Artificial Neural Networks - ANNs) הוכיחו את עצמם כמודלים פרמטריים מאד יעילים לפתרון מגוון רחב של בעיות. הההשראה לצורה שבה המודלים הפרמטריים בנויים מגיעה מרשתות עצביות ביולוגיות כגון המוח ורשת העצבים. בצורה מאד פשטנית ניתן לתאר את האופן בו תא עצב (נוירון) ביולוגי פועל כך:

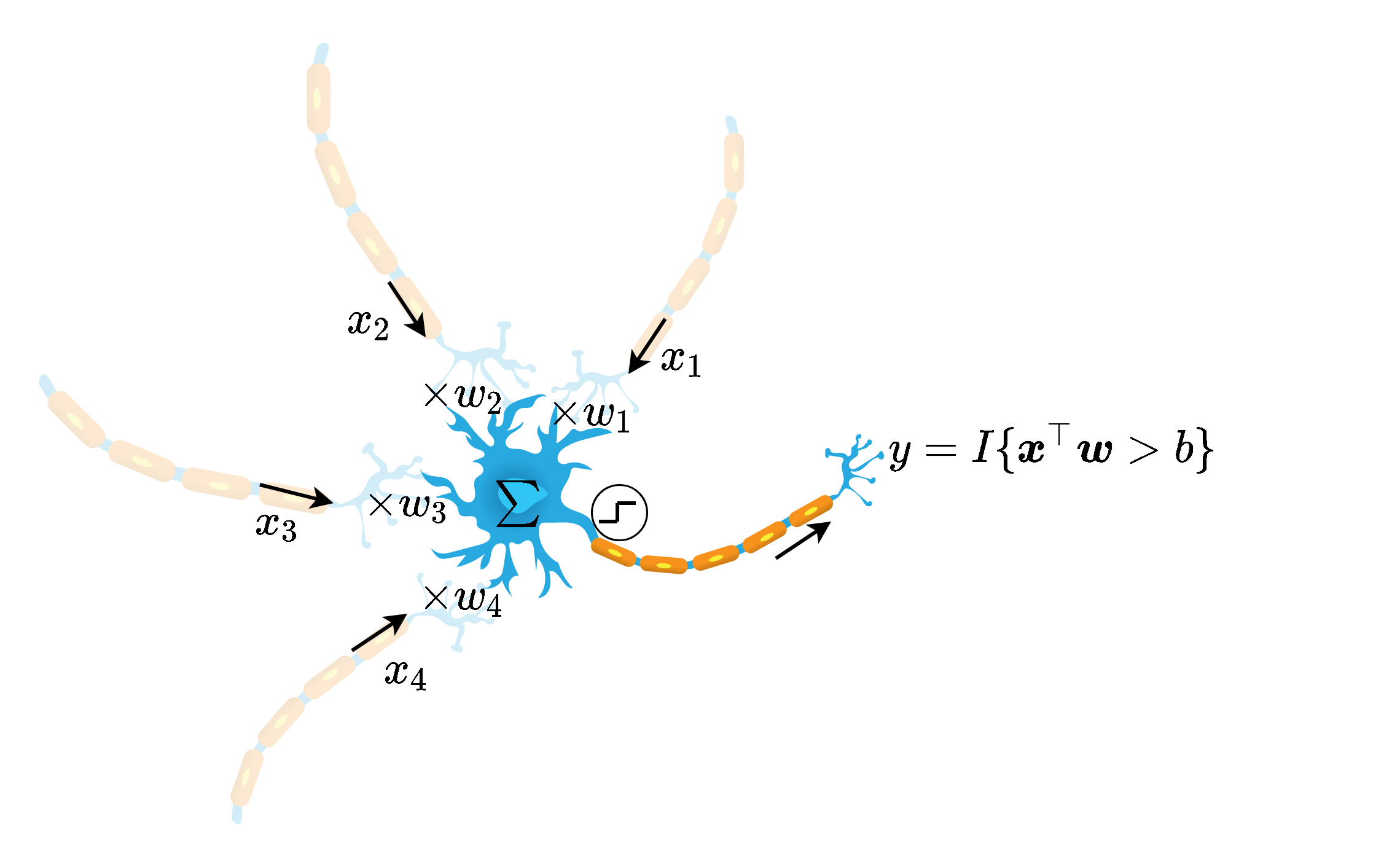
לנוירון האופייני ישנו איזור של "קולטנים" (Dendrites) אשר משמשים כקלט של הנוירון, ומעין זרוע אשר יכולה להתחבר ל"קולטנים" של ניורונים אחרים (אשר חיבורים הנקראים Axons) והיא משמשת לפלט של ההנוירון. הקלט והפלט של הנוירונים הוא פולסים חשמליים אשר הנוירונים יכולים לקבל ולשלוח אחד לשני. כל נוירון מסתכל על סך כל הפולסים שהוא מקבל מהנוירונים האחרים. כאשר סך כל הפולסים עובר ערך סף מסויים, הוא "יורה" פולס משלו למוצא של הנוירון.

התיאור הזה הוא מאד מופשט ומפספס הרבה מהמורכבויות של אופן פעולת הנוירונים אך הוא ההשראה למודל של רשתות נוירונים מלאכותיות. באופן סכימתי ניתן למדל את פעולת הנוירון באופן הבא:

$$y=I\{\boldsymbol{x}^{\top}\boldsymbol{w}+b>0\}$$

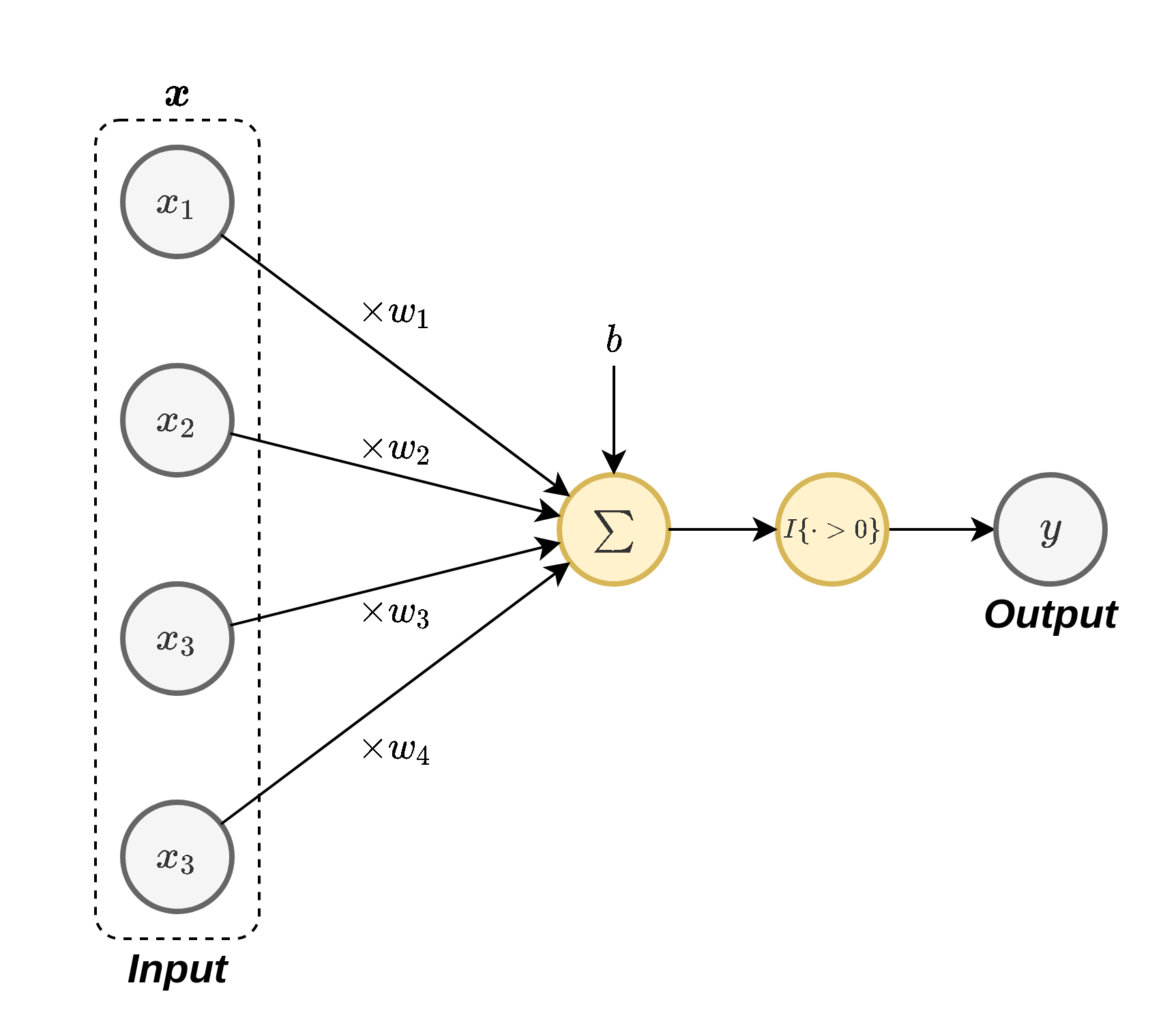
בשלב הראשון מחשבים קומבינציה לינארית של הכניסות עם משקלים כל שהם $w_i$ ובתוספת היסט $b$ ובשלב השני מעבירים את הקומבינציה הלינארית דרך פונקציית מדרגה אשר מוציאה 1 אם הקומבינציה הלינארית חיובית ו0 אחרת.

נוירונים ברשת נוירונים מלאכותית

המודל של הנוירון הביולוגי עומד בבסיס של המודל של רשתות נוירונים מלאכותיות אך עם תיקון קטן. לצורך של בניה ולימוד של מודל פרמטרי פונקציית המדרגה היא בפועל מאד בעייתית. זאת בעיקר משום שהיא מוסגלת להוציא רק ערכים בינאריים ובגלל העובדה שהנגזרת שלה היא 0 בכל מקום, מה שלא יאפשר לנו ללמוד את הפרמטרים של המודל שנבנה בעזרת gradient descent. לשם כך נחליף את פונקציית המדרגה בפונקציה אחרת כלשהיא $\varphi(\cdot)$. פונקציה זו מכונה פונקציית ההפעלה (activation function). בחירות נפוצות של פונקציית ההפעלה כוללות את

• הפונקציה הלוגיסטית (סיגמואיד): $\varphi(x)=\sigma(x)=\frac{1}{1+e^{-x}}$
• טנגנס היפרבולי: $\varphi(x)=\tanh\left(x/2\right)$
• פונקציית ה ReLU (Rectified Linear Unit): אשר מוגדרת $\varphi(x)=\max(x,0)$ (זוהי פונקציית ההפעלה הנפוצה ביותר כיום).

פונקציות נוספות אשר נמצאות כיום בשימוש, כוללות כל מיני וריאציות שונות שנעשו על פונקציית ה ReLU.

באופן סכימתי נסמן נוירון בודד באופן הבא:

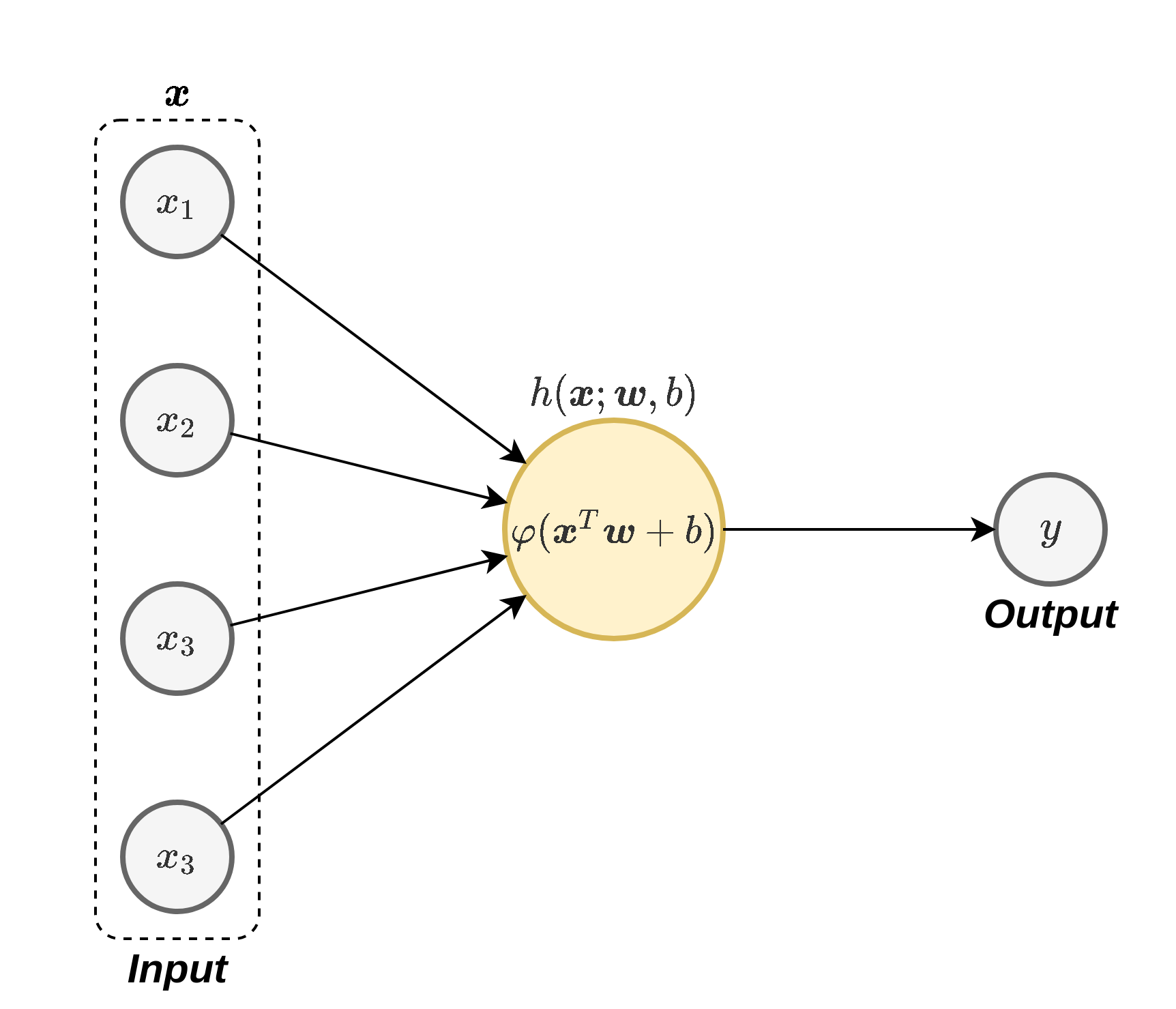
כאשר סימנו את הפונקציה שאותה מבצע הנוירון ב $h$ עם פרמטרים $\boldsymbol{w}$ ו $b$. נרצה כעת להשתמש במודל של הנוירון בודד כדי לבנות רשת המורכבת ממספר נוירונים אשר בעזרתה נוכל למדל פונקציות מורכבות.

רשת נוירונים

בדומה למקרה הביולוגי, לנוירון בודד אין הרבה שימוש, אך כאשר משלבים מספר רב של נוירונים ניתן לייצג בעזרתם פונקציות מאד מורכבות. בדומה לרשתות הביולוגיות אנו נחבר את הנוירונים כך שהמוצאים של הניורונים ישמשו ככניסות של נוירונים אחרים כפי שמתואר בשרטוט הבא:

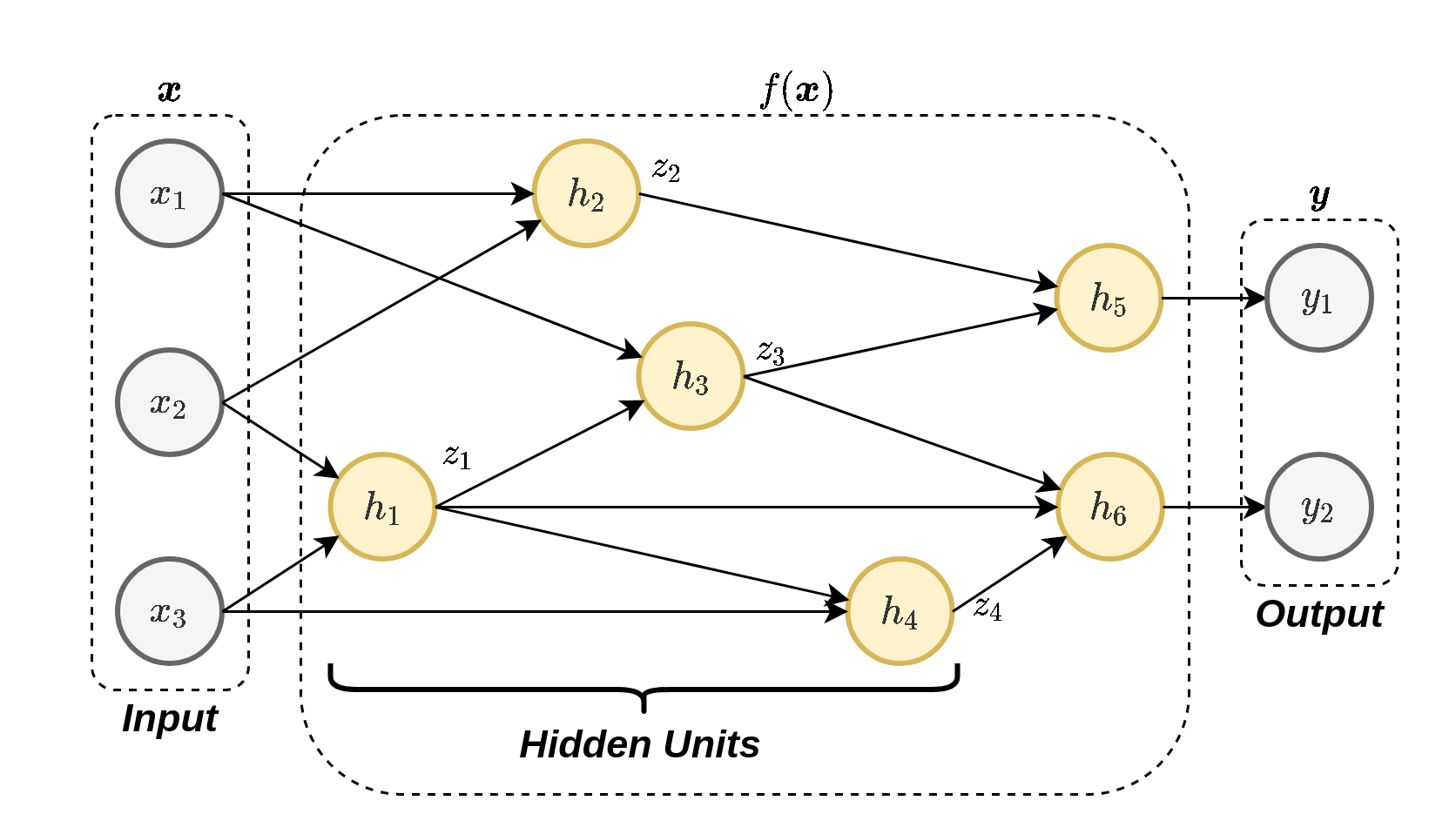
על ידי בניית רשת שכזו ניתן לקבל מודל פרמטרי בעלי יכולת לקרב מגוון מאד רחב של פונקציות. הפרמטרים של המודל יהיו אוסף כל הפרמטרים של כל הנוירונים ברשת. לרוב הנוירונים אשר מרכיבים את הרשת יהיו מצורה שהצגנו קודם:

$$h_j(\boldsymbol{x};\boldsymbol{w}_j,b_j)=\varphi(\boldsymbol{x}^{\top}\boldsymbol{w}_j+b_j)$$

אך באופן כללי ניתן גם לבחור לבנות את הרשת מפונקציות אחרות. בקורס זה, אלא אם נאמר אחרת, אנו נניח כי כי הנוירונים הם מהצורה שהופיעה לעיל. לשם הנוחות, אנו נסמן לרוב (בדומה לשאר הקורס) ב $\boldsymbol{\theta}$ את הוקטור אשר מכיל את כל הפרמטרים של המודל:

$$\boldsymbol{\theta}=[\boldsymbol{w}_1^{\top},b_1,\boldsymbol{w}_2^{\top},b_2,\dots]^{\top}$$

הארכיטקטורה של הרשת

המבנה של הרשת כולל את מספר הנוירונים שהיא מכילה ואת הדרך שבה הם מחוברים אחד לשני נקרא הארכיטקטורה של הרשת. בחירת הארכיטקטורה של הרשת היא קריטית מאד לטיב הביצועים שנקבל ולשימושים שונים מתאימות ארכיטקטורות שונות. חלק גדול מאד מהמחקר שנעשה כיום בתחום הוא סביב הנושא של חיפוש ארכיטקטורות אשר מניבות תוצאות טובות יותר לשימושים ספציפיים. התהליך של מציאת הארכיטקטורה שמתאימה לבעיה דורש לא מעט ניסיון, אינטואיציה, והרבה ניסוי וטעיה כנגד ה validation set. לרוב הדרך הטובה ביותר לבחור ארכיטקטורה היא למצוא בעיה דומה לבעיה שאותה ברצונכם לפתור והשתמש בארכיטקטורה שעבדה טוב במקרה זה (לרפרנס).

נגדיר שני מושגים אשר קשורים לארכיטקטורה של הרשת:

• יחידות נסתרות (hidden units): הנוירונים אשר אינם מחוברים למוצא הרשת (אינם נמצאים בסוף הרשת).
• רשת עמוקה (deep network): רשת אשר מכילה מסלולים מהכניסה למוצא, אשר עוברים דרך יותר מיחידה נסתרת אחת.

לדוגמא, ברשת בשרטוט מעל הנוירונים $h_1$ עד $h_4$ הם יחידות ניסתרות והרשת נחשבת לרשת עמוקה משום שהמסלול שעובר דרך $h_1$, $h_4$ ו $h_6$ עובד דרך שתי יחידות נסתרות.

Feed-forward vs. Recurrent

אנו מבדילים בין שני סוגי ארכיטקטורות:

• רשת הזנה קדמית (feed-forward network): ארכיטקטורות אשר אינן מכילות מסלולים מעגליים. ברשתות אלו ניתן להגדיר את הכיוון בו זורם המידע מהכניסה ליציאה ואת הסדר של הנוירונים ברשת. רוב הרשתות אשר נמצאות בשימוש בכיום הם מסוג זה.
• רשתות נשנות (recurrent neural network - RNN): בקורס זה לא נעסוק ברשתות מסוג זה, נציין רק שאלו ארכיטקטורות אשר כן מכילות מסלולים מעגליים. רשתות אלו יכילו לרוב גם רכיבי זיכרון (בדומה ל registers במעגלים חשמליים) והם יתאימו למקרים בהם $\boldsymbol{x}$ מאד ארוך, כמו לדוגמא במקרה של אות אודיו ארוך.

על החשיבות של פונקציות ההפעלה

ללא פונקציות ההפעלה, הנוירונים פשוט יחשבו קומבינציות לינאריות של הקלט שהם מקבלים. מכיוון שכל הרכבה של פונקציות לינאריות עדיין נשארת פונקציה לינארית, אנו נקבל שהרשת תמיד תוכל לייצג רק פונקציות לינאריות, ללא תלות בארכיטקטורה שאותה נבחר. לכן חוסר הלינאריות של פונקציות ההפעלה הוא למעשה מה שמאפשר בפועל לרשתות הנוירונים לייצג מגוון עשיר של פונקציות.

המוצא של הרשת

Regression + ERM

כאשר נשתמש ברשת לפתרון של בעיות רגרסיה בשיטת ERM, אנו נרצה שהרשת תמדל את החזאי אשר אמור להוציא סקלר אשר מקבל ערכים רציפים, לרוב בתחום לא מוגבל. במקרה זה אנו נרצה שהמוצא של הרשת יתנקז לנוירון בודד ללא פונקציית אקטיבציה (על מנת שלא להגביל את המוצא של הרשת).

בעיות סיווג בגישה הדיסקרימינטיבית הסתברותית

לסיווג בינארי, בגישה הדיסקרימינטיבית ההסתברותית, אנו נרצה למדל את $p_{\text{y}|\mathbf{x}}(1|\boldsymbol{x})$. לכן, אנו נרצה שהרשת תוציא ערך סקלרי רציף בתחום בין 0 ל-1. לכן גם פה אנו נרצה שהמוצא של הרשת יתנקז לנוירון בודד עם פונקציית הפעלה אשר מוציאה ערכים בתחום $[0,1]$ כדוגמאת הפונקציה הלוגיסטית. (ניתן לחילופין לחשב על המודל כעל רשת ללא פוקציית הפעלה במוצא אשר מפעילים על המוצא של הרשת את הפונקציה לוגיסטית על מנת לקבל הסתברות חוקית).

בסיווג לא בינארי של $C$ מחלקות, בגישה הדטרמיניסטית ההסתברותית, אנו נרצה למדל את כל ההסתברויות של $p_{\text{y}|\mathbf{x}}(y|\boldsymbol{x})$. לכן אנו נרצה שהרשת תוציא וקטור באורך $C$ שעליו נפעיל את פונקציית ה softmax, על מנת לקבל וקטור הסתברות חוקי.

מציאת הפרמטרים של המודל

כתלות בבעיה אותה אנו מנסים לפתור, והשיטה שבה אנו משתמשים, אנו נרשום את בעיית האופטימיזציה שאותה אנו רוצים לפתור. בהקשר של השיטות הרלוונטיות בקורס זה:

• ב ERM אנו ננסה למזער את ה risk האמפירי.
• בגישה הדיסקרימינטיבית ההסתברותית נשתמש ב MLE או MAP.

בדומה למקרה של logistic regression גם כאן לרוב לא נוכל לפתור את בעיית האופטימיזציה על ידי גזירה והשוואה ל-0 ובמקום זה נחפש פתרון על ידי שימוש ב gradient descent. בשביל לחשב את הגרדיאנט לפי הפרמטרים אנו נעזר בשיטה שנקראת back-propagation, אותה נציג בהמשך ההרצאה הזו.

עבור רשת את מואצה נסמן בתור $f(x;W)\in\mathbb{R}$.

רגרסיה: לדוגמה, פונקציית ההפסד של least squares היא

$$\mathcal{L}(W)=\sum_{i=1}^{n}\left(y^{(i)}-f\left(x^{(i)};W\right)\right)^{2}$$

סיווג בינארי: במקרה של רגרסיה לוגיסטית ניתן להשתמש בפונקציה מהרצאה 9:

$$\mathcal{L}(W)=-\sum_{i=1}^{N}\left[y^{(i)}\log\left(\sigma\left(f\left(x^{(i)};W\right)\right)\right)+\left(1-y^{(i)}\right)\log\left(1-\sigma\left(f\left(x^{(i)};W\right)\right)\right)\right]$$

עם פונקציית הסיגמואיד $\sigma(z)=1/\left(1+\exp(-z)\right)$.

במקרה של סיווג רב מחלקתי $f(x;W)=\left(f_{1}(x;W),\ldots,f_{c}(x;W)\right)\in\mathbb{R}^{C}$, ניתן להשתמש בפונקציית softmax ופונקציית ההפסד מהרצאה 9.

MultiLayer Perceptron (MLP)

נתמקד כעת בארכיטקטורה מאד נפוצה אשר נקראת MultiLayer Perceptron (MLP). בארכיטקטורה זו הנוירונים מסודרים בשתי שכבות (layers) או יותר, המכונות Fully Connected (FC) layers. בהן כל נוירון מוזן מכל הנוירונים שבשכבה שלפניו. לדוגמא:

מה שמגדיר את הארכיטקטורה במקרה של MLP הוא מספר השכבות וכמות הנוירונים בכל שכבה. כמות הנוירונים בכל שכבה מכונה לרוב הרוחב של השכבה. בדוגמה הזו, יש ברשת 3 שכבות ברוחב 2, 3 ו 2.

רישום מטריצי

בשרטוט מעל סימנו את הנוירון ה $j$ בשכבה ה $i$ ב $h_{i,j}$ ואת המוצא שלו ב $z_{i,j}$. בנוסף, סימנו את הוקטור המכיל את כל המוצאים בשיכבה ה $i$ ב $z_i$. נסמן גם את הפרמטרים של הנוירון ה $i,j$ ב $\boldsymbol{w}_{i,j}$ ו $b_{i,j}$. הפונקציה שאותה מבצע כל נוירון הינה:

$$z_{i,j}=h_{i,j}(z_{i-1,j};\boldsymbol{w}_{i,j},b_{i,j})=\varphi(\boldsymbol{z}_{i,j}^{\top}\boldsymbol{w}_{i,j}+b_{i,j})$$

כדי לרשום את הפעולה שמבצעת כל שיכבה בצורה מטריצית נגדיר את המטריצה $W_i$ אשר מאגדת את כל הוקטורים $\boldsymbol{w}_{i,j}$ באותה שכבה:

$$W_i= \begin{bmatrix} -&\boldsymbol{w}_{i,1}&-\\ -&\boldsymbol{w}_{i,2}&-\\ &\vdots&\\ \end{bmatrix}$$

ונגדיר באופן דומה את הוקטור $\boldsymbol{b}_i$ אשר מאגד את כל הפרמטרים $b_{i,j}$ באותה שכבה:

$$\boldsymbol{b}_i=[b_{i,1},b_{i,2},\dots]^{\top}$$

נוכל כעת לרשום את הפעולה שמבצעת כל השכבה כולה באופן הבא:

$$\boldsymbol{z}_i=\varphi(W_i\boldsymbol{z}_{i-1}+\boldsymbol{b}_i)$$

כאשר פונקציית ההפעלה $\varphi$ פועלת על וקטור איבר-איבר.

עבור MLP כללי עם $L$ שכבות ניתן לכתוב

$$z_{L}=\varphi_{L}\left(W_{L}z_{L-1}+b_{L}\right)=\varphi_{L}\left(W_{L}\varphi_{L-1}\left(W_{L-1}z_{L-2}+b_{L-1}\right)\right)=h_{L}\circ h_{L-1}\circ\cdots\circ h_{1}(x)$$

כאשר

$$h_{\ell}\left(z_{\ell-1}\right)=\varphi_{\ell}\left(W_{\ell}z_{\ell-1}+b_{\ell}\right)$$

שימו לב, $\varphi_{\ell}$ יכולה להיות תלויה בשכבה.

ניתן לכתוב זאת בצורה רקורסיבית

$$\begin{aligned}\mathbf{z}_{0} & =\mathbf{x}\\ \mathbf{u}_{\ell} & =W_{\ell}\mathbf{z}_{l-1}+\mathbf{b}_{\ell}\quad\text{for }l=1\text{ to }L\\ \mathbf{z}_{\ell} & =\varphi_{\ell}(\mathbf{u}_{\ell})\quad\text{for }l=1\text{ to }L \end{aligned}$$

כאשר פעולת האקטיבציה $\varphi_{\ell}$ מתבצעת איבר-איבר ו-$\mathbf{y}_{L}=\mathbf{z}_{L}$.

הערה לגבי נגזרות וקטוריות

זכרו כי עבור פונקציה סקלרית $f(\boldsymbol{\theta}),\boldsymbol{\theta}\in\mathbb{R}^{n}$

$$\nabla f(\theta)=\frac{\partial f(\theta)}{\partial\theta}=\left[\frac{\partial f(\theta)}{\partial\theta_{1}},\ldots,\frac{\partial f(\theta)}{\partial\theta_{n}}\right]\in\mathbb{R}^{1\times n}$$

תהי $\boldsymbol{g}(\boldsymbol{\theta})$ פונקציה וקטורית של וקטור $\mathbf{\boldsymbol{\theta}}$, $\mathbf{g}:\mathbf{\theta}\mapsto\mathbb{R}^{m}$, $\mathbf{g}(\mathbf{\boldsymbol{\theta}})=\left(g_{1}(\mathbf{\mathbf{\boldsymbol{\theta}}}),\ldots,g_{m}(\mathbf{\boldsymbol{\theta}})\right)$.

אזי

$$\frac{\partial\mathbf{g}(\boldsymbol{\theta})}{\partial\boldsymbol{\theta}}=\left[\frac{\partial g_{i}(\boldsymbol{\theta})}{\partial\theta_{j}}\right]_{ij}\in\mathbb{R}^{m\times n}$$

ובמקרה הפשוט בו $\mathbf{g}(\boldsymbol{\theta})=\left(g_{1}(\theta_{1}),\ldots,g_{m}(\theta_{m})\right)$ מתקיים כי

$$\frac{\partial\mathrm{\mathbf{g}}(\boldsymbol{\theta})}{\partial\boldsymbol{\theta}}=\mathrm{diag}\left(g'_{1}(\theta_{1}),\ldots,g'_{m}(\theta_{m})\right)=\mathrm{diag}\left(g'\left(\boldsymbol{\theta}\right)\right)$$

מקור השם

השם Perceprton מתייחס לאלגוריתם / שיטה ישנה אשר אינה נלמדת בקורס זה. ה Perceptron היה אחד הנסיונות הראשונים למדל נוירון ולהשתמש בו לפתרון בעיות במערכות לומדות אך ההצלחה שלו הייתה מאד מוגבלת. למרות שהשם MLP עשוי לרמוז אחרת, אין באמת קשר בין אלגוריתם / מודל ה Perceptron לארכיטקטורת ה MLP שתיארנו כאן. (אם אתם רוצים להשתכנע תוכלו לשמוע פה את Geoffrey Hinton, שנתן לארכיטקטורה זו את שמה, אומר זאת בעצמו).

יכולת היצוג של MLP - "משפט הקירוב האוניברסלי"

המשפט הבא מובא ללא הוכחה והוא מתייחס ליכולת של MLP עם שיכבה ניסתרת אחת לקרב כל פונקציה חסומה ורציפה:

בהינתן:

• כל פונקציית הפעלה רציפה $\varphi$ שאינה פולינומיאלית (או כזו חסומה ואינטגרבילית).
• וכל פונקציה רציפה על קוביית היחידה $f:[0,1]^{D_{\text{in}}}\rightarrow[0,1]^{D_{\text{out}}}$.

אזי:

ניתן למצוא פונקציה $f_{\varepsilon}:[0,1]^{D_{\text{in}}}\rightarrow[0,1]^{D_{\text{out}}}$ מהצורה (MLP עם שיכבה נסתרת אחת):

$$f_{\varepsilon}(\boldsymbol{x})=W_2\varphi(W_1\boldsymbol{x}+\boldsymbol{b}_1)+\boldsymbol{b}_2$$

כך ש:

$$\underset{x\in[0,1]^{D_{\text{in}}}}{\text{sup}}\lVert f(\boldsymbol{x})-f_{\varepsilon}(\boldsymbol{x}) \rVert<\varepsilon$$

הערה: משפט זה לא מגביל את הרוחב של השכבה הנסתרת וכמובן שככל שהפונקציה $f$ מורכבת יותר כך נצטרך לרוב שכבה רחבה יותר. משפט זה הוא בעיקר יעיל כדי להבין את יכולת הייצוג החזקה של רשתות ניורונים, והוא לא מאד שימושי ליישומים פרקטיים.

Back-Propagation

באופן כללי אנו צריכים לחשב את הנגזרות של פונקציית ההפסד ביחס לכל פרמטרי הרשת (משקולות ואיברי הטיה), כלומר

$$\frac{\mathcal{\partial L}(W)}{\partial W_{\ell}}$$

כאשר $W_{\ell}$ הם המשקולות של השכבה ה-$\ell$. שימו לב כי

$$\begin{aligned} \frac{\mathcal{\partial L}(W)}{\partial W_{\ell}} &=\frac{\mathcal{\partial L}(W)}{\partial z_{\ell}}\frac{\partial z_{\ell}}{\partial W_{\ell}}=\frac{\mathcal{\partial L}(W)}{\partial z_{\ell}}\frac{\partial z_{\ell}}{\partial u_{\ell}}\frac{\partial u_{\ell}}{\partial W_{\ell}} \\ \frac{\partial\mathbf{u}_{\ell}}{\partial W_{\ell}} & =\mathbf{z}_{\ell-1}\\ \frac{\partial\mathbf{z}_{\ell}}{\partial\mathbf{u}_{\ell}} & =\mathrm{diag}\left(\varphi'_{\ell}\left(\mathbf{u}_{\ell}\right)\right) \end{aligned}$$

כאשר הנגזרת המאתגרת היחידה לחישוב היא הראשונה.

כפי שציינו קודם, לרוב אנו נמצא את הפרמטרים של המודל בעזרת gradient descent. כדי להקל על החישוב של הנגזרות של ה objective לפי הפרמטרים אנו נשתמש בשיטה הנקראת back-propagation אשר מחשבת את הגרדיאנטים על ידי שימוש בכלל השרשרת.

כלל השרשרת מפרק את הנגזרת של הרכבה של פונקציות למכפלה של הנזגרות של הפונקציות. במקרה של משתנה יחיד היא נראית כך:

$$\left(f(g(x))\right)'=f'(g(x))\cdot g'(x)$$

במקרה של מספר משתנים הוא נראה כך:

$$\begin{aligned} \frac{d}{dx} f(z_1(x),z_2(x),z_3(x)) =& &\left(\frac{\partial}{\partial z_1} f(z_1(x),z_2(x),z_3(x))\right)\frac{d}{dx}z_1(x)\\ &+&\left(\frac{\partial}{\partial z_2} f(z_1(x),z_2(x),z_3(x))\right)\frac{d}{dx}z_2(x)\\ &+&\left(\frac{\partial}{\partial z_3} f(z_1(x),z_2(x),z_3(x))\right)\frac{d}{dx}z_3(x)\\ \end{aligned}$$

אנו נראה שעל מנת לחשב את הנגזרות לפי הפרמטרים של הנוירונים ברשת אנו נצטרך לבצע 2 שלבים:

• Forward pass: העברה של הדגימות במדגם דרך הרשת ושמירה של כל ערכי הביניים (המוצאים של כל הנוירונים).
• Backward pass: חישוב של הנגזרות של הנוירונים מהמוצא של הרשת לכיוון הכניסה.

על מנת להסביר את השיטה נסתכל על 2 דוגמאות.

דוגמא פשוטה

נרצה לחשב את $\partial\mathcal{L}/\partial\theta_{i}$ עבור פרמטר $\theta_{i}$ כלשהו. למשל, עבור פונקציית ההפסד הריבועית $L=(y-t)^{2},$ כאשר $t$ הוא הערך האמיתי

$$\frac{\partial L}{\partial\theta_{i}}=2\left(y-t\right)\frac{\partial y}{\partial\theta_{i}}$$

ובאופן דומה עובר שאר פונקציות ההפסד. כך, עלינו להתמקד בנגזרת זאת.

נתחיל ראשית במקרה סקלרי פשוט שבו יש 4 פונקציות פרמטריות שמורכבות אחת אחרי השניה:

נרשום את הנגזרת של $y$ לפי $\theta_2$. על פי כלל השרשרת נוכל לרשום את הנגזרת באופן הבא:

$$\frac{\partial y}{\partial\theta_2}=\frac{\partial y}{\partial z_2}\frac{\partial z_2}{\partial\theta_2}=\frac{\partial y}{\partial z_2}\frac{\partial}{\partial \theta_2}h_2(z_1;\theta_2)$$

נוכל לפרק גם את הנגזרת של $\frac{\partial y}{\partial z_2}$ לפי כלל השרשרת:

$$\frac{\partial y}{\partial z_2}=\frac{\partial y}{\partial z_3}\frac{\partial z_3}{\partial z_2}=\frac{\partial}{\partial z_3}h_4(z_3;\theta_4)\frac{\partial}{\partial z_2}h_3(z_2;\theta_3)$$

לכן:

$$\frac{\partial y}{\partial \theta_2}=\frac{\partial y}{\partial z_3}\frac{\partial z_3}{\partial z_2}=\frac{\partial}{\partial z_3}h_4(z_3;\theta_4)\frac{\partial}{\partial z_2}h_3(z_2;\theta_3)\frac{\partial}{\partial \theta_2}h_2(z_1;\theta_2)$$

כדי לחשב את הביטוי שקיבלנו עלינו לבצע את שני השלבים הבאים:

• לחשב את כל ה $z_i$ לאורך הרשת (forward pass).
• לחשב את כל הנגזרות מהמוצא של הרשת ועד לנקודה בה נמצא הפרמטר שלפיו רוצים לגזור (backward-pass).

דוגמא מעט יותר מורכבת

נסתכל על הרשת הבאה:

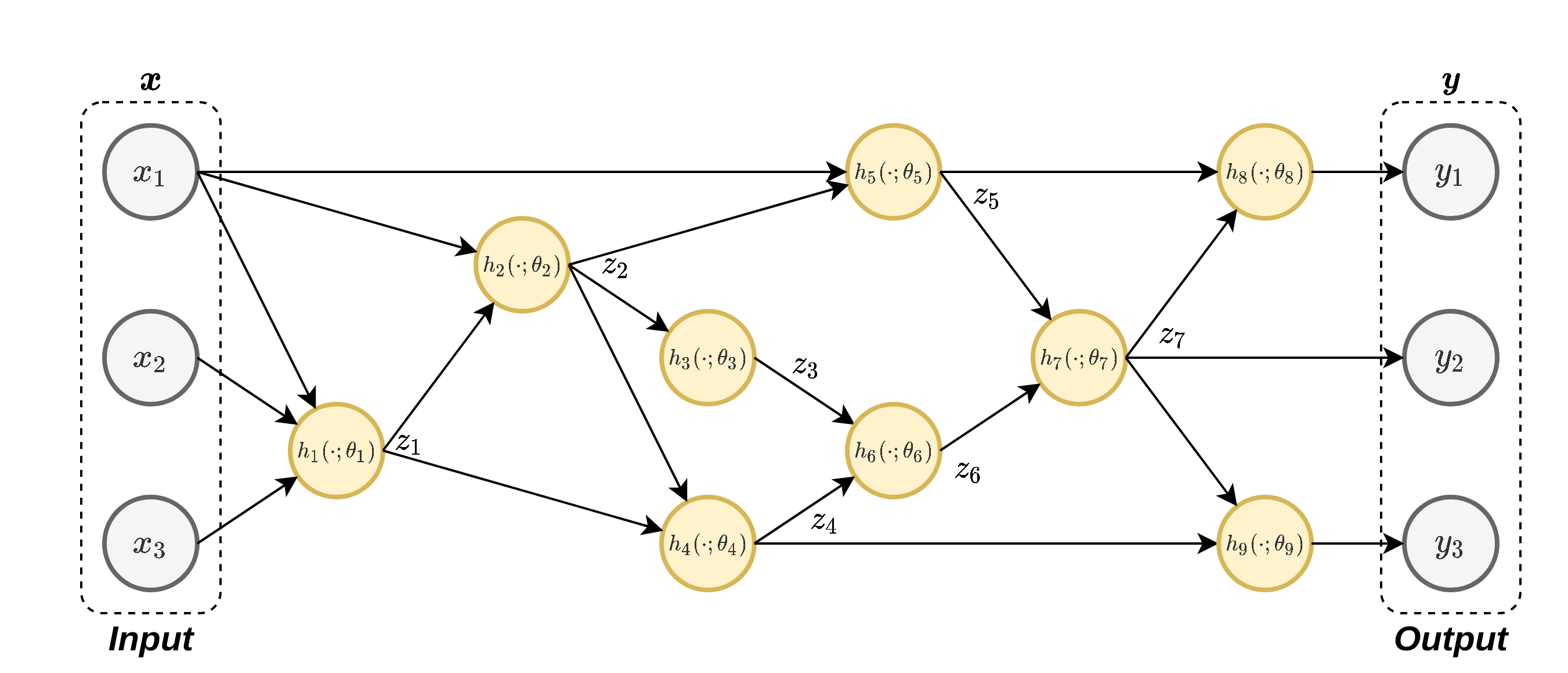
נחשב לדוגמא את הנגזרת של $y_1$ לפי $\theta_3$.

נפרק על פי כלל השרשרת את הנגזרת של $\frac{\partial y_1}{\partial \theta_3}$ בדומה למה שחישבנו קודם:

$$\frac{\partial y_1}{\partial \theta_3} =\frac{\partial y_1}{\partial z_7}\frac{\partial z_7}{\partial z_6}\frac{\partial z_6}{\partial z_3}\frac{\partial z_3}{\partial \theta_3} =\frac{\partial}{\partial z_7}h_8(z_7;\theta_8)\frac{\partial}{\partial z_6}h_7(z_6;\theta_7)\frac{\partial}{\partial z_3}h_6(z_5;\theta_6)\frac{\partial}{\partial \theta_3}h_3(z_2;\theta_3)$$

• נריץ את ה forward-pass בשביל לחשב את ערכי ה $z_i$.
• נריץ את ה backward-pass בו נחשב את הנגזרות מהמוצא של הרשת עד לנגזרת של $h_3$.