הרצאה 8 - שיערוך פילוג בשיטות פרמטריות וסיווג גנרטיבי
דוגמא
נניח שאנו רוצים לחזות האם אדם מסויים פרק את הכתף על פי הסימפטומים שלו. לשם כך נסתכל על המדגם הבא
פריקה
כאב בכתף
נפיחות
סימנים כחולים
נימול ביד
נזלת
1
+
+
+
+
+
-
2
+
+
+
+
-
-
3
+
+
+
-
+
-
4
+
+
+
+
-
+
5
-
-
-
-
-
-
6
-
+
-
-
-
+
7
-
-
-
+
-
-
8
-
+
-
-
-
-
האם לאדם עם כל הסימפטומים יש פריקה של הכתף?
שיערוך נאיבי - חוסר תלות בין המשתנים
נניח שאנו רוצים לשערך צפיפות הסתברות של משתנה D D D
p x ( x ) = p x 1 ( x 1 ) p x 2 ( x 2 ) … p x D ( x D ) = ∏ d = 1 D p x d ( x d ) p_{\mathbf{x}}(\boldsymbol{x})=
p_{\text{x}_1}(x_1)
p_{\text{x}_2}(x_2)
\dots
p_{\text{x}_D}(x_D)
=\prod_{d=1}^D p_{\text{x}_d}(x_d) p x ( x ) = p x 1 ( x 1 ) p x 2 ( x 2 ) … p x D ( x D ) = d = 1 ∏ D p x d ( x d )
חיסרון: שהיא מגבילה מאד את הפילוגים שניתן ללמוד.
מסווג בייס נאיבי - Naïve Bayes Classification
תזכורת במשימות סיווג קיים x ∈ R D \mathbf{x}\in R^D x ∈ R D y ∈ { 1 , 2 , . . . , C } \text{y}\in\{1,2,...,C\} y ∈ { 1 , 2 , . . . , C } P ( x , y ) P(\mathbf{x},\text{y}) P ( x , y )
נוכל להשתמש בשערוך הנאיבי לפתרון בעיות סיווג.
נניח כי:
p x ∣ y ( x ∣ y ) = p x 1 ∣ y ( x 1 ∣ y ) p x 2 ∣ y ( x 2 ∣ y ) … p x D ∣ y ( x D ∣ y ) = ∏ d = 1 D p x d ∣ y ( x d ∣ y ) p_{\mathbf{x}|\text{y}}(\boldsymbol{x}|y)=
p_{\text{x}_1|\text{y}}(x_1|y)
p_{\text{x}_2|\text{y}}(x_2|y)
\dots
p_{\text{x}_D|\text{y}}(x_D|y)
=\prod_{d=1}^D p_{\text{x}_d|\text{y}}(x_d|y) p x ∣ y ( x ∣ y ) = p x 1 ∣ y ( x 1 ∣ y ) p x 2 ∣ y ( x 2 ∣ y ) … p x D ∣ y ( x D ∣ y ) = d = 1 ∏ D p x d ∣ y ( x d ∣ y )
זו כמובן הנחה מאוד פשטנית שאינה מתקיימת במציאות.
אנו לא נרצה להניח חוסר תלות בין x \mathbf{x} x y \text{y} y
מסווג בייס נאיבי - Naïve Bayes Classification
החזאי אשר ממזער את הסיכוי לטעות יהיה:
y ^ = h ( x ) = arg max y p y ∣ x ( y ∣ x ) = arg max y p x ∣ y ( x ∣ y ) p y ( y ) = arg max y p y ( y ) ∏ d = 1 D p x d ∣ y ( x d ∣ y ) \begin{aligned}
\hat{y}=h(\boldsymbol{x})
&=\underset{y}{\arg\max}\ p_{\text{y}|\boldsymbol{x}}(y|\boldsymbol{x})\\
&=\underset{y}{\arg\max}\ p_{\boldsymbol{x}|\text{y}}(\boldsymbol{x}|y)p_{\text{y}}(y)\\
&=\underset{y}{\arg\max}\ p_{\text{y}}(y)\prod_{d=1}^D p_{\text{x}_d|\text{y}}(x_d|y)
\end{aligned} y ^ = h ( x ) = y arg max p y ∣ x ( y ∣ x ) = y arg max p x ∣ y ( x ∣ y ) p y ( y ) = y arg max p y ( y ) d = 1 ∏ D p x d ∣ y ( x d ∣ y )
מסווג בייס נאיבי - Naïve Bayes Classification
האיור מתוך, C.M. Bishop, Pattern Recognition and Machine Learning
דוגמא 1 - זיהוי פריקה של הכתף
תחת הנחת חוסר התלות נשערך בנפרד את ההסתברות המותנית של כל אחד מהרכיבים p x d ∣ y ( x d ∣ y ) , x d ∈ { 0 , 1 } p_{\text{x}_d|\text{y}}(x_d|y), x_d\in\{0,1\} p x d ∣ y ( x d ∣ y ) , x d ∈ { 0 , 1 }
p x pain ∣ y ( x pain ∣ 1 ) = { 4 4 = 1 1 0 4 = 0 0 p_{\text{x}_{\text{pain}}|\text{y}}(x_{\text{pain}}|1)=\begin{cases}
\tfrac{4}{4}=1&1\\
\tfrac{0}{4}=0&0
\end{cases} p x pain ∣ y ( x pain ∣ 1 ) = { 4 4 = 1 4 0 = 0 1 0 p x pain ∣ y ( x pain ∣ 0 ) = { 2 4 = 0.5 1 2 4 = 0.5 0 p_{\text{x}_{\text{pain}}|\text{y}}(x_{\text{pain}}|0)=\begin{cases}
\tfrac{2}{4}=0.5&1\\
\tfrac{2}{4}=0.5&0
\end{cases} p x pain ∣ y ( x pain ∣ 0 ) = { 4 2 = 0 . 5 4 2 = 0 . 5 1 0 p x swelling ∣ y ( x swelling ∣ 1 ) = { 4 4 = 1 1 0 4 = 0 0 p_{\text{x}_{\text{swelling}}|\text{y}}(x_{\text{swelling}}|1)=\begin{cases}
\tfrac{4}{4}=1&1\\
\tfrac{0}{4}=0&0
\end{cases} p x swelling ∣ y ( x swelling ∣ 1 ) = { 4 4 = 1 4 0 = 0 1 0 p x swelling ∣ y ( x swelling ∣ 0 ) = { 0 4 = 0 1 1 4 = 1 0 p_{\text{x}_{\text{swelling}}|\text{y}}(x_{\text{swelling}}|0)=\begin{cases}
\tfrac{0}{4}=0&1\\
\tfrac{1}{4}=1&0
\end{cases} p x swelling ∣ y ( x swelling ∣ 0 ) = { 4 0 = 0 4 1 = 1 1 0 ובאופן דומה לשאר הרכיבים.
דוגמא 1 - זיהוי פריקה של הכתף
החיזוי עבור המקרה בו מופיעים כל הסימפטומים יהיה
y ^ = arg max y p y ( y ) ∏ d = 1 D p x d ∣ y ( 1 ∣ y ) \hat{y}
=\underset{y}{\arg\max}\ p_{\text{y}}(y)\prod_{d=1}^D p_{\text{x}_d|\text{y}}(1|y) y ^ = y arg max p y ( y ) d = 1 ∏ D p x d ∣ y ( 1 ∣ y ) זאת אומרת שעלינו לבדוק האם:
p y ( 1 ) ∏ d = 1 D p x d ∣ y ( 1 ∣ 1 ) > ? p y ( 0 ) ∏ d = 1 D p x d ∣ y ( 1 ∣ 0 ) 0.5 × 1 × 1 × 0.75 × 0.5 × 0.25 > ? 0.5 × 0.5 × 0 × 0.25 × 0 × 0.25 0.09375 > ? 0 \begin{aligned}
p_{\text{y}}(1)\prod_{d=1}^D p_{\text{x}_d|\text{y}}(1|1)\overset{?}{>}
&p_{\text{y}}(0)\prod_{d=1}^D p_{\text{x}_d|\text{y}}(1|0)\\
0.5 \times 1 \times 1 \times 0.75 \times 0.5 \times 0.25 \overset{?}{>}
&0.5 \times 0.5 \times 0 \times 0.25 \times 0 \times 0.25\\
0.09375 \overset{?}{>}
& 0
\end{aligned} p y ( 1 ) d = 1 ∏ D p x d ∣ y ( 1 ∣ 1 ) > ? 0 . 5 × 1 × 1 × 0 . 7 5 × 0 . 5 × 0 . 2 5 > ? 0 . 0 9 3 7 5 > ? p y ( 0 ) d = 1 ∏ D p x d ∣ y ( 1 ∣ 0 ) 0 . 5 × 0 . 5 × 0 × 0 . 2 5 × 0 × 0 . 2 5 0 מכיוון שתנאי זה מתקיים, החיזוי יהיה שישנה פריקה של כתף.
דוגמא 2 - זיהוי הונאות אשראי
ננסה להשתמש בשיטה זו לבעיית חיזוי הונאות האשראי
שיטות פרמטריות
דומה לשימוש שעשינו במודלים פרמטריים בגישה הדטרמיניסטית.
נגביל את הצורה של הפונקציה שאותה אנו רוצים לשערך למודל פרמטרי.
נסמן את וקטור הפרמטרים ב θ \boldsymbol{\theta} θ
כאן המודל חייב לייצר פילוג חוקי עבור כל בחירה של פרמטרים.
מגבלה קשה אשר מצמצמת מאד את המודלים הפרמטריים שאיתם ניתן לעבוד.
בחירת הפרמטרים
נרצה למצוא דרך לתת "ציון" לכל בחירה של פרמטרים ולחפש את הפרמטרים אשר מניבים את הציון הטוב ביותר.
נציג שתי גישות שונות להתייחס לפרמטרים של המודל.
כל גישה מובילה לדרך מעט שונה לבחירה של הפרמטרים.
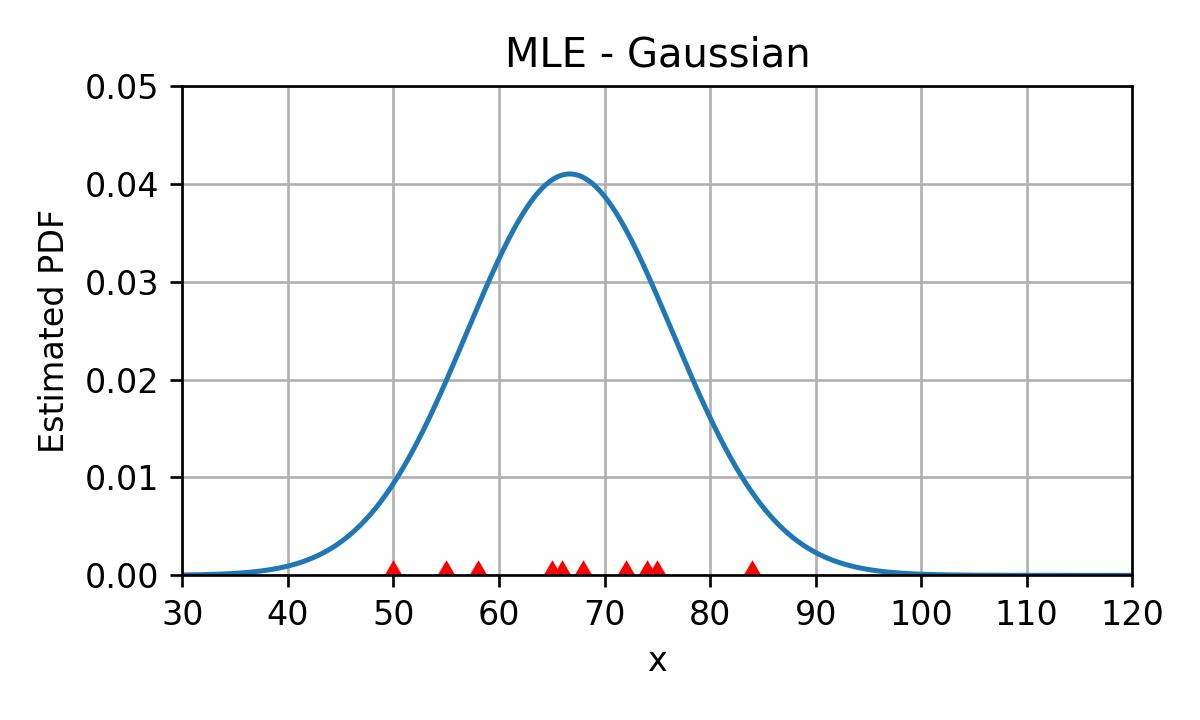
דוגמא: שיערוך הפילוג של זמן הנסיעה
D = { x ( i ) } = { 55 , 68 , 75 , 50 , 72 , 84 , 65 , 58 , 74 , 66 } \mathcal{D}=\{x^{(i)}\}=\{55, 68, 75, 50, 72, 84, 65, 58, 74, 66\} D = { x ( i ) } = { 5 5 , 6 8 , 7 5 , 5 0 , 7 2 , 8 4 , 6 5 , 5 8 , 7 4 , 6 6 } משערך ה KDE של הפילוג (לא דנו הסמסטר) הינו:
נרצה לשערך פרמטרים של פילוג נורמלי שיתאר בצורה טובה את הדגימות במדגם.
הגישה הלא-בייסיאניתFrequentist ))
p x ( x ; θ ) p_{\mathbf{x}}(\boldsymbol{x};\boldsymbol{\theta}) p x ( x ; θ )
נתייחס לפרמטרים כאל מספרים שאותם יש לקבוע על מנת שהמודל יתאר בצורה טובה את המדגם.
ההנחה היא כי יש ערך לא ידוע של הפרמטר שהוא ה"טוב" ביותר.
Maximum Likelyhood Estimator (MLE)
נסמן ב p D ( D ; θ ) p_{\mathcal{D}}(\mathcal{D};\boldsymbol{\theta}) p D ( D ; θ ) D = { x ( i ) } \mathcal{D}=\{\boldsymbol{x}^{(i)}\} D = { x ( i ) }
גודל זה מכונה הסבירות (likelihood ) של המדגם.
אנו מעוניינים למצוא את הפרמטרים θ \boldsymbol{\theta} θ
מקובל לסמן את פונקציית ה likelihood באופן הבא:
L ( θ ; D ) ≜ p D ( D ; θ ) \mathcal{L}(\boldsymbol{\theta};\mathcal{D})\triangleq p_{\mathcal{D}}(D;\boldsymbol{\theta}) L ( θ ; D ) ≜ p D ( D ; θ ) משערך ה MLE של θ \boldsymbol{\theta} θ
θ ^ MLE = arg max θ L ( θ ; D ) \hat{\boldsymbol{\theta}}_{\text{MLE}}
=\underset{\boldsymbol{\theta}}{\arg\max}\ \mathcal{L}(\boldsymbol{\theta};\mathcal{D}) θ ^ MLE = θ arg max L ( θ ; D )
Maximum Likelyhood Estimator (MLE)
θ ^ MLE = arg max θ L ( θ ; D ) \hat{\boldsymbol{\theta}}_{\text{MLE}}
=\underset{\boldsymbol{\theta}}{\arg\max}\ \mathcal{L}(\boldsymbol{\theta};\mathcal{D}) θ ^ MLE = θ arg max L ( θ ; D )
נרשום את בעיית האופטימיזציה כבעיית מינימיזציה:
θ ^ MLE = arg min θ − L ( θ ; D ) \hat{\boldsymbol{\theta}}_{\text{MLE}}
=\underset{\boldsymbol{\theta}}{\arg\min}\ -\mathcal{L}(\boldsymbol{\theta};\mathcal{D}) θ ^ MLE = θ arg min − L ( θ ; D )
כאשר הדגימות במדגם הם i.i.d:
p D ( D ; θ ) = ∏ i p x ( x ( i ) ; θ ) p_{\mathcal{D}}(\mathcal{D};\boldsymbol{\theta})=\prod_i p_{\mathbf{x}}(\boldsymbol{x}^{(i)};\boldsymbol{\theta}) p D ( D ; θ ) = i ∏ p x ( x ( i ) ; θ ) ולכן:
θ ^ MLE = arg min θ − L ( θ ; D ) = arg min θ − ∏ i p x ( x ( i ) ; θ ) \hat{\boldsymbol{\theta}}_{\text{MLE}}
=\underset{\boldsymbol{\theta}}{\arg\min}\ -\mathcal{L}(\boldsymbol{\theta};\mathcal{D})
=\underset{\boldsymbol{\theta}}{\arg\min}\ -\prod_i p_{\mathbf{x}}(\boldsymbol{x}^{(i)};\boldsymbol{\theta}) θ ^ MLE = θ arg min − L ( θ ; D ) = θ arg min − i ∏ p x ( x ( i ) ; θ )
Maximum Likelyhood Estimator (MLE)
θ ^ MLE = arg min θ − L ( θ ; D ) = arg min θ − ∏ i p x ( x ( i ) ; θ ) \hat{\boldsymbol{\theta}}_{\text{MLE}}
=\underset{\boldsymbol{\theta}}{\arg\min}\ -\mathcal{L}(\boldsymbol{\theta};\mathcal{D})
=\underset{\boldsymbol{\theta}}{\arg\min}\ -\prod_i p_{\mathbf{x}}(\boldsymbol{x}^{(i)};\boldsymbol{\theta}) θ ^ MLE = θ arg min − L ( θ ; D ) = θ arg min − i ∏ p x ( x ( i ) ; θ ) במקרים רבים נוכל להחליף את המכפלה על כל הדגימות בסכום, על ידי החלפת פונקציית ה likelihood ב log-likelihood:
θ ^ MLE = arg min θ − log L ( θ ; D ) = arg min θ − ∑ i log ( p x ( x ( i ) ; θ ) ) \hat{\boldsymbol{\theta}}_{\text{MLE}}
=\underset{\boldsymbol{\theta}}{\arg\min}\ -\log\mathcal{L}(\boldsymbol{\theta};\mathcal{D})
=\underset{\boldsymbol{\theta}}{\arg\min}\ -\sum_i \log\left(p_{\mathbf{x}}(\boldsymbol{x}^{(i)};\boldsymbol{\theta})\right) θ ^ MLE = θ arg min − log L ( θ ; D ) = θ arg min − i ∑ log ( p x ( x ( i ) ; θ ) ) הערה: בקורסים "עיבוד אותות אקראיים" ו-"הסקה סטטיסטית" מרחיבים הרבה בנושא תכונות משערך זה ואחרים.
דוגמא - זמן הנסיעה
ננסה להתאים למדגם מודל של פילוג נורמלי:
p x ( x ; θ ) = 1 2 π σ exp ( − ( x − μ ) 2 2 σ 2 ) p_{\text{x}}(x;\boldsymbol{\theta})=\frac{1}{\sqrt{{2\pi}}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) p x ( x ; θ ) = 2 π σ 1 exp ( − 2 σ 2 ( x − μ ) 2 ) וקטור הפרמטרים הינו θ = [ μ , σ ] ⊤ \boldsymbol{\theta}=[\mu,\sigma]^\top θ = [ μ , σ ] ⊤
דוגמא - זמן הנסיעה
p x ( x ; θ ) = 1 2 π σ exp ( − ( x − μ ) 2 2 σ 2 ) p_{\text{x}}(x;\boldsymbol{\theta})=\frac{1}{\sqrt{{2\pi}}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) p x ( x ; θ ) = 2 π σ 1 exp ( − 2 σ 2 ( x − μ ) 2 ) נרשום את בעיית האופטימיזציה של מציאת משערך ה MLE:
θ ^ MLE = arg min θ − ∑ i log ( p x ( x ( i ) ; θ ) ) = arg min θ − ∑ i log ( 1 2 π σ exp ( − ( x ( i ) − μ ) 2 2 σ 2 ) ) = arg min θ ∑ i log ( σ ) + 1 2 log ( 2 π ) + ( x ( i ) − μ ) 2 2 σ 2 = arg min θ N log ( σ ) + 1 2 σ 2 ∑ i ( x ( i ) − μ ) 2 \begin{aligned}
\hat{\boldsymbol{\theta}}_{\text{MLE}}
&=\underset{\boldsymbol{\theta}}{\arg\min}\ -\sum_i \log\left(p_{\text{x}}(x^{(i)};\boldsymbol{\theta})\right)\\
&=\underset{\boldsymbol{\theta}}{\arg\min}\ -\sum_i \log\left(\frac{1}{\sqrt{{2\pi}}\sigma}\exp\left(-\frac{(x^{(i)}-\mu)^2}{2\sigma^2}\right)\right)\\
&=\underset{\boldsymbol{\theta}}{\arg\min}\ \sum_i \log(\sigma) + \tfrac{1}{2}\log(2\pi) + \frac{(x^{(i)}-\mu)^2}{2\sigma^2}\\
&=\underset{\boldsymbol{\theta}}{\arg\min}\ N\log(\sigma) + \frac{1}{2\sigma^2}\sum_i (x^{(i)}-\mu)^2\\
\end{aligned} θ ^ MLE = θ arg min − i ∑ log ( p x ( x ( i ) ; θ ) ) = θ arg min − i ∑ log ( 2 π σ 1 exp ( − 2 σ 2 ( x ( i ) − μ ) 2 ) ) = θ arg min i ∑ log ( σ ) + 2 1 log ( 2 π ) + 2 σ 2 ( x ( i ) − μ ) 2 = θ arg min N log ( σ ) + 2 σ 2 1 i ∑ ( x ( i ) − μ ) 2 נפתור על ידי גזירה והשוואה ל-0.
דוגמא - זמן הנסיעה
נסמן את ה objective ב f f f
f ( θ ; x ) = N log ( σ ) + 1 2 σ 2 ∑ i ( x ( i ) − μ ) 2 f(\boldsymbol{\theta};\mathcal{x})=N\log(\sigma) + \frac{1}{2\sigma^2}\sum_i (x^{(i)}-\mu)^2 f ( θ ; x ) = N log ( σ ) + 2 σ 2 1 i ∑ ( x ( i ) − μ ) 2 { ∂ f ( θ ; x ) ∂ μ = 0 ∂ f ( θ ; x ) ∂ σ = 0 ⇔ { − 1 σ 2 ∑ i ( x ( i ) − μ ) = 0 N σ − 1 σ 3 ∑ i ( x ( i ) − μ ) 2 = 0 ⇔ { N μ − ∑ i x ( i ) = 0 N σ 2 − ∑ i ( x ( i ) − μ ) 2 = 0 ⇔ { μ = 1 N ∑ i x ( i ) σ 2 = 1 N ∑ i ( x ( i ) − μ ) 2 \begin{aligned}
&\begin{cases}
\frac{\partial f(\boldsymbol{\theta};\mathcal{x})}{\partial\mu} = 0\\
\frac{\partial f(\boldsymbol{\theta};\mathcal{x})}{\partial\sigma} = 0
\end{cases}\\
\Leftrightarrow&\begin{cases}
-\frac{1}{\sigma^2}\sum_i (x^{(i)}-\mu)=0\\
\frac{N}{\sigma}-\frac{1}{\sigma^3}\sum_i (x^{(i)}-\mu)^2=0
\end{cases}\\
\Leftrightarrow&\begin{cases}
N\mu-\sum_i x^{(i)}=0\\
N\sigma^2-\sum_i (x^{(i)}-\mu)^2=0
\end{cases}\\
\Leftrightarrow&\begin{cases}
\mu=\frac{1}{N}\sum_i x^{(i)}\\
\sigma^2=\frac{1}{N}\sum_i (x^{(i)}-\mu)^2
\end{cases}\\
\end{aligned} ⇔ ⇔ ⇔ { ∂ μ ∂ f ( θ ; x ) = 0 ∂ σ ∂ f ( θ ; x ) = 0 { − σ 2 1 ∑ i ( x ( i ) − μ ) = 0 σ N − σ 3 1 ∑ i ( x ( i ) − μ ) 2 = 0 { N μ − ∑ i x ( i ) = 0 N σ 2 − ∑ i ( x ( i ) − μ ) 2 = 0 { μ = N 1 ∑ i x ( i ) σ 2 = N 1 ∑ i ( x ( i ) − μ ) 2
דוגמא - זמן הנסיעה
במקרה של הנסיעות בכביש החוף נקבל:
μ = 66.7 [min] \mu=66.7\ \text{[min]} μ = 6 6 . 7 [min] σ = 9.7 [min] \sigma=9.7\ \text{[min]} σ = 9 . 7 [min]
הגישה הבייסיאנית
הפרמטרים של המודל הם ריאליזציות (הגרלות) של משתנה אקראי.
גישה זו מניחה שיש בידינו מודל לפילוג המשותף של הפרמטרים והמדגם.
p D , θ ( D , θ ) = p D ∣ θ ( D ∣ θ ) p θ ( θ ) p_{\mathcal{D},\boldsymbol{\theta}}(\mathcal{D},\boldsymbol{\theta})
=p_{\mathcal{D}|\boldsymbol{\theta}}(\mathcal{D}|\boldsymbol{\theta})p_{\boldsymbol{\theta}}(\boldsymbol{\theta}) p D , θ ( D , θ ) = p D ∣ θ ( D ∣ θ ) p θ ( θ ) תחת ההנחה שבהינתן הפרמטרים הדגימות במדגם הם i.i.d:
p D , θ ( D , θ ) = p θ ( θ ) ∏ i p x ∣ θ ( x ( i ) ∣ θ ) p_{\mathcal{D},\boldsymbol{\theta}}(\mathcal{D},\boldsymbol{\theta})
=p_{\boldsymbol{\theta}}(\boldsymbol{\theta})\prod_i p_{\mathbf{x}|\boldsymbol{\theta}}(\boldsymbol{x}^{(i)}|\boldsymbol{\theta}) p D , θ ( D , θ ) = p θ ( θ ) i ∏ p x ∣ θ ( x ( i ) ∣ θ )
עלינו לקבוע את p x ∣ θ ( x ∣ θ ) p_{\mathbf{x}|\boldsymbol{\theta}}(\boldsymbol{x}|\boldsymbol{\theta}) p x ∣ θ ( x ∣ θ ) p θ ( θ ) p_{\boldsymbol{\theta}}(\boldsymbol{\theta}) p θ ( θ )
זכרו בשבגישה הקודמת הנחנו כי θ \theta θ
הגישה הבייסיאנית
A Prioiri Distribution
הפילוג השולי של הפרמטרים p θ ( θ ) p_{\boldsymbol{\theta}}(\boldsymbol{\theta}) p θ ( θ ) פילוג הפריורי (prior distribution ) או הא-פריורי (a priori distribution ), זאת אומרת הפילוג של θ \boldsymbol{\theta} θ
A Posteriori Distribution
הפילוג של הפרמטרים בהינתן המדגם p , θ ∣ D ( θ ∣ D ) p_{,\boldsymbol{\theta}|\mathcal{D}}(\boldsymbol{\theta}|\mathcal{D}) p , θ ∣ D ( θ ∣ D ) פילוג הפוסטריורי (posterior distribution ) או א-פוסטריורי (a posteriori distribution ) (או הפילוג בדיעבד), זאת אומרת, הפילוג אחרי שראינו את המדגם.
Maximum A-posteriori Probaility (MAP)
MAP משערך את הערך אשר ממקסם את הפילוג הא-פוסטריורי (הערך הכי סביר של θ \boldsymbol{\theta} θ p θ ∣ D ( θ ∣ D ) p_{\boldsymbol{\theta}|\mathcal{D}}(\boldsymbol{\theta}|\mathcal{D}) p θ ∣ D ( θ ∣ D )
θ ^ MAP = arg max θ p θ ∣ D ( θ ∣ D ) = arg min θ − p θ ∣ D ( θ ∣ D ) \hat{\boldsymbol{\theta}}_{\text{MAP}}
=\underset{\boldsymbol{\theta}}{\arg\max}\ p_{\boldsymbol{\theta}|\mathcal{D}}(\boldsymbol{\theta}|\mathcal{D})
=\underset{\boldsymbol{\theta}}{\arg\min}\ -p_{\boldsymbol{\theta}|\mathcal{D}}(\boldsymbol{\theta}|\mathcal{D}) θ ^ MAP = θ arg max p θ ∣ D ( θ ∣ D ) = θ arg min − p θ ∣ D ( θ ∣ D ) על פי חוק בייס, נוכל לכתוב זאת כ:
θ ^ MAP = arg min θ − p D ∣ θ ( D ∣ θ ) p θ ( θ ) p D ( D ) = arg min θ − p D ∣ θ ( D ∣ θ ) p θ ( θ ) \hat{\boldsymbol{\theta}}_{\text{MAP}}
=\underset{\boldsymbol{\theta}}{\arg\min}\
-\frac{
p_{\mathcal{D}|\boldsymbol{\theta}}(\mathcal{D}|\boldsymbol{\theta})
p_{\boldsymbol{\theta}}(\boldsymbol{\theta})
}{
p_{\mathcal{D}}(\mathcal{D})
}
=\underset{\boldsymbol{\theta}}{\arg\min}\
-p_{\mathcal{D}|\boldsymbol{\theta}}(\mathcal{D}|\boldsymbol{\theta})
p_{\boldsymbol{\theta}}(\boldsymbol{\theta}) θ ^ MAP = θ arg min − p D ( D ) p D ∣ θ ( D ∣ θ ) p θ ( θ ) = θ arg min − p D ∣ θ ( D ∣ θ ) p θ ( θ ) כאשר הדגימות במדגם בהינתן θ \boldsymbol{\theta} θ
θ ^ MAP = arg min θ − p θ ( θ ) ∏ i p x ∣ θ ( x ( i ) ∣ θ ) \hat{\boldsymbol{\theta}}_{\text{MAP}}
=\underset{\boldsymbol{\theta}}{\arg\min}\
-p_{\boldsymbol{\theta}}(\boldsymbol{\theta})
\prod_i p_{\mathbf{x}|\boldsymbol{\theta}}(\boldsymbol{x}^{(i)}|\boldsymbol{\theta}) θ ^ MAP = θ arg min − p θ ( θ ) i ∏ p x ∣ θ ( x ( i ) ∣ θ )
Maximum A-posteriori Probaility (MAP)
θ ^ MAP = arg min θ − p θ ( θ ) ∏ i p x ∣ θ ( x ( i ) ∣ θ ) \hat{\boldsymbol{\theta}}_{\text{MAP}}
=\underset{\boldsymbol{\theta}}{\arg\min}\
-p_{\boldsymbol{\theta}}(\boldsymbol{\theta})
\prod_i p_{\mathbf{x}|\boldsymbol{\theta}}(\boldsymbol{x}^{(i)}|\boldsymbol{\theta}) θ ^ MAP = θ arg min − p θ ( θ ) i ∏ p x ∣ θ ( x ( i ) ∣ θ ) גם כאן נוכל להפוך את המכפלה לסכום על ידי מזעור מינוס הלוג של הפונקציה:
θ ^ MAP = arg min θ − log ( p θ ( θ ) ) − ∑ i log ( p x ∣ θ ( x ( i ) ∣ θ ) ) \hat{\boldsymbol{\theta}}_{\text{MAP}}
=\underset{\boldsymbol{\theta}}{\arg\min}\ -\log\left(p_{\boldsymbol{\theta}}(\boldsymbol{\theta})\right)-\sum_i \log\left(p_{\mathbf{x}|\boldsymbol{\theta}}(\boldsymbol{x}^{(i)}|\boldsymbol{\theta})\right) θ ^ MAP = θ arg min − log ( p θ ( θ ) ) − i ∑ log ( p x ∣ θ ( x ( i ) ∣ θ ) )
ההבדל בין MLE ל MAP
θ ^ MLE = arg min θ − ∑ i log ( p x ( x ( i ) ; θ ) ) \hat{\boldsymbol{\theta}}_{\text{MLE}}
=\underset{\boldsymbol{\theta}}{\arg\min}\ -\sum_i \log\left(p_{\mathbf{x}}(\boldsymbol{x}^{(i)};\boldsymbol{\theta})\right) θ ^ MLE = θ arg min − i ∑ log ( p x ( x ( i ) ; θ ) ) θ ^ MAP = arg min θ − log ( p θ ( θ ) ) − ∑ i log ( p x ∣ θ ( x ( i ) ∣ θ ) ) \hat{\boldsymbol{\theta}}_{\text{MAP}}
=\underset{\boldsymbol{\theta}}{\arg\min}\ -\log\left(p_{\boldsymbol{\theta}}(\boldsymbol{\theta})\right)-\sum_i \log\left(p_{\mathbf{x}|\boldsymbol{\theta}}(\boldsymbol{x}^{(i)}|\boldsymbol{\theta})\right) θ ^ MAP = θ arg min − log ( p θ ( θ ) ) − i ∑ log ( p x ∣ θ ( x ( i ) ∣ θ ) )
האיבר − log ( p θ ( θ ) ) -\log\left(p_{\boldsymbol{\theta}}(\boldsymbol{\theta})\right) − log ( p θ ( θ ) ) θ \boldsymbol{\theta} θ
ראינו תוספת שכזו כאשר דיברנו על רגולריזציה.
ניתן לחשוב על בעיית ה MAP כעל בעיית MLE עם רגולריזציה.
בתרגיל הבית אתם תראו את השקילות שבין בעיית MAP לבין לבעיית MLE עם רגולריזציה.
בגישה בייסיאנית השערוך הוא בעיית חיזוי
אנו מתייחסים גם למדגם וגם לפרמטרים בריאליזציות של משתנים אקראיים.
אנו מניחים שאנו יודעים את הפילוג המשותף שלהם.
ואנו מנסים למצוא את הערך של הפרמטרים בהינתן המדגם.
זוהי בדיוק בעיית חיזוי קלאסית של משתנה אקראי אחד בהינתן משתנה אקראי אחר על סמך הפילוג המשותף.
דוגמא - הוספת prior
נחזור לדוגמא של התאמת מודל של פילוג נורמלי לפילוג של זמן הנסיעה בכביש החוף.
לשם הפשטות נקבע את סטיית התקן של המודל ל σ = 10 \sigma=10 σ = 1 0
הפרמטר היחיד של המודל יהיה μ \mu μ
p x ∣ μ ( x ∣ μ ) = 1 2 π σ exp ( − ( x − μ ) 2 2 σ 2 ) p_{\text{x}|\mu}(x|\mu)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) p x ∣ μ ( x ∣ μ ) = 2 π σ 1 exp ( − 2 σ 2 ( x − μ ) 2 )
דוגמא - הוספת prior
p x ∣ μ ( x ∣ μ ) = 1 2 π σ exp ( − ( x − μ ) 2 2 σ 2 ) p_{\text{x}|\mu}(x|\mu)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) p x ∣ μ ( x ∣ μ ) = 2 π σ 1 exp ( − 2 σ 2 ( x − μ ) 2 )
נניח שיש לנו ידע קודם על פילוג הצפוי של μ \mu μ
נניח שהפילוג הא-פריורי של μ \mu μ μ μ = 60 \mu_{\mu}=60 μ μ = 6 0 σ μ = 5 \sigma_{\mu}=5 σ μ = 5
p μ ( μ ) = 1 2 π σ μ exp ( − ( μ − μ μ ) 2 2 ⋅ σ μ 2 ) p_{\mu}(\mu)=\frac{1}{\sqrt{2\pi}\sigma_{\mu}}\exp\left(-\frac{(\mu-\mu_{\mu})^2}{2\cdot\sigma_{\mu}^2}\right) p μ ( μ ) = 2 π σ μ 1 exp ( − 2 ⋅ σ μ 2 ( μ − μ μ ) 2 ) נרשום את משערך ה MAP של μ \mu μ
μ ^ MAP = arg min μ − log ( p μ ( μ ) ) − ∑ i log ( p x ∣ μ ( x ( i ) ∣ μ ) ) \begin{aligned}
\hat{\mu}_{\text{MAP}}
=\underset{\mu}{\arg\min}\ -\log\left(p_{\mu}(\mu)\right)-\sum_i \log\left(p_{\mathbf{x}|\mu}(\boldsymbol{x}^{(i)}|\mu)\right)
\end{aligned} μ ^ MAP = μ arg min − log ( p μ ( μ ) ) − i ∑ log ( p x ∣ μ ( x ( i ) ∣ μ ) )
דוגמא - הוספת prior
μ ^ MAP = arg min μ − log ( p μ ( μ ) ) − ∑ i log ( p x ∣ μ ( x ( i ) ∣ μ ) ) \begin{aligned}
\hat{\mu}_{\text{MAP}}
=\underset{\mu}{\arg\min}\ -\log\left(p_{\mu}(\mu)\right)-\sum_i \log\left(p_{\mathbf{x}|\mu}(\boldsymbol{x}^{(i)}|\mu)\right)
\end{aligned} μ ^ MAP = μ arg min − log ( p μ ( μ ) ) − i ∑ log ( p x ∣ μ ( x ( i ) ∣ μ ) ) גזירה והשוואה ל-0 נותנת את התוצאה הבאה:
∂ f ( θ ; x ) ∂ μ = 0 ⇔ 1 σ μ 2 ( μ − μ μ ) − 1 σ 2 ∑ i ( x ( i ) − μ ) = 0 ⇔ ( 1 σ μ 2 + N σ 2 ) μ = μ μ σ μ 2 + 1 σ 2 ∑ i x ( i ) ⇔ μ = σ 2 N σ μ 2 μ μ + 1 N ∑ i x ( i ) σ 2 N σ μ 2 + 1 \begin{aligned}
\frac{\partial f(\boldsymbol{\theta};\mathcal{x})}{\partial\mu} &= 0\\
\Leftrightarrow
\frac{1}{\sigma_{\mu}^2}(\mu-\mu_{\mu})-\frac{1}{\sigma^2}\sum_i (x^{(i)}-\mu)&=0\\
\Leftrightarrow
\left(\frac{1}{\sigma_{\mu}^2}+\frac{N}{\sigma^2}\right)\mu&=\frac{\mu_{\mu}}{\sigma_{\mu}^2}+\frac{1}{\sigma^2}\sum_i x^{(i)}\\
\Leftrightarrow
\mu&=\frac{\frac{\sigma^2}{N\sigma_{\mu}^2}\mu_{\mu}+\frac{1}{N}\sum_i x^{(i)}}{\frac{\sigma^2}{N\sigma_{\mu}^2}+1}
\end{aligned} ∂ μ ∂ f ( θ ; x ) ⇔ σ μ 2 1 ( μ − μ μ ) − σ 2 1 i ∑ ( x ( i ) − μ ) ⇔ ( σ μ 2 1 + σ 2 N ) μ ⇔ μ = 0 = 0 = σ μ 2 μ μ + σ 2 1 i ∑ x ( i ) = N σ μ 2 σ 2 + 1 N σ μ 2 σ 2 μ μ + N 1 ∑ i x ( i ) זו למעשה ממוצע ממושקל בין הממוצע של x x x μ μ \mu_{\mu} μ μ
דוגמא - הוספת prior
עבור הדוגמא שלנו נקבל:
μ = 64.8 [min] \mu=64.8\ \text{[min]} μ = 6 4 . 8 [min] ערך זה מעט יותר קרוב ל60 מאשר התוצאה שקיבלנו בשיערוך ה MLE. זאת משום ה prior ש"מושך" את הפרמטרים לאיזורים הסבירים יותר ולכן הוא מקרב אותו ל μ μ = 60 \mu_{\mu}=60 μ μ = 6 0
שימוש בשיערוך פרמטרי לפתרון בעיות supervised learning
נראה עכשיו איך להשתמש בשערוך הצפיפות שתארנו צורך פתרון בעיות סיווג בלמידה מפוקחת. נציג שיטה אשר משתמשת במודל של פילוג נורמלי וב MLE לפתרון בעיות סיווג.
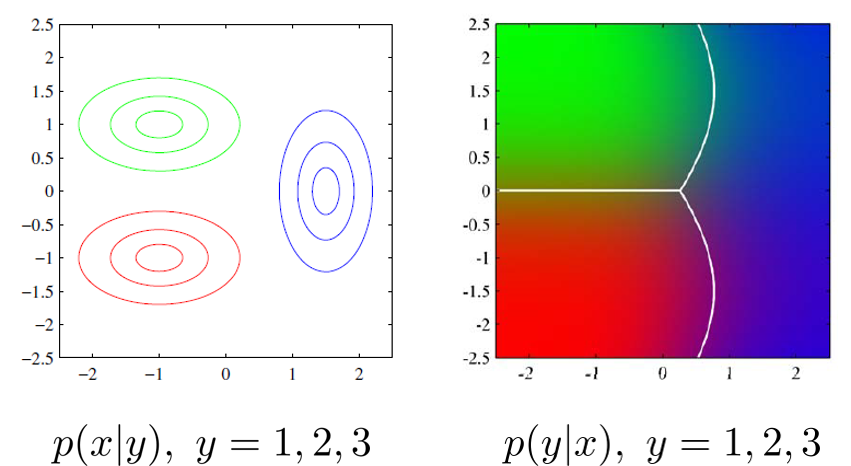
Quadratic Discriminant Analysis (QDA)
p x ∣ y ( x ∣ c ; μ c , Σ c ) = 1 ( 2 π ) D ∣ Σ c ∣ exp ( − 1 2 ( x − μ c ) ⊤ Σ c − 1 ( x − μ c ) ) p_{\mathbf{x}|\text{y}}(\boldsymbol{x}|c;\boldsymbol{\mu}_c,\Sigma_c)=
\frac{1}{\sqrt{(2\pi)^D|\Sigma_c|}}
\exp\left(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu}_c)^{\top}\Sigma_c^{-1}(\boldsymbol{x}-\boldsymbol{\mu}_c)\right) p x ∣ y ( x ∣ c ; μ c , Σ c ) = ( 2 π ) D ∣ Σ c ∣ 1 exp ( − 2 1 ( x − μ c ) ⊤ Σ c − 1 ( x − μ c ) ) הפילוג המשותף של x \mathbf{x} x y \text{y} y
p x , y ( x , y ; { μ c } , { Σ c } ) = p x ∣ y ( x ∣ y ; μ y , Σ y ) p y ( y ) p_{\mathbf{x},\text{y}}(\boldsymbol{x},y;\{\boldsymbol{\mu}_c\},\{\Sigma_c\})=
p_{\mathbf{x}|\text{y}}(\boldsymbol{x}|y;\boldsymbol{\mu}_y,\Sigma_y)
p_{\text{y}}(y) p x , y ( x , y ; { μ c } , { Σ c } ) = p x ∣ y ( x ∣ y ; μ y , Σ y ) p y ( y )
Quadratic Discriminant Analysis (QDA)
בעיית האופטימיזציה של MLE תהיה:
θ ^ MLE = arg min θ − log L ( θ ; D ) = arg min θ − ∑ i log ( p x ∣ y ( x ( i ) ∣ y ( i ) ; μ y , Σ y ) p y ( y ( i ) ) ) = arg min θ − ∑ i log ( p x ∣ y ( x ( i ) ∣ y ( i ) ; μ y , Σ y ) ) + log ( p y ( y ( i ) ) ) = arg min θ − ∑ i log ( p x ∣ y ( x ( i ) ∣ y ( i ) ; μ y , Σ y ) ) \begin{aligned}
\hat{\boldsymbol{\theta}}_{\text{MLE}}
&=\underset{\boldsymbol{\theta}}{\arg\min}\ -\log\mathcal{L}(\boldsymbol{\theta};\mathcal{D})\\
&=\underset{\boldsymbol{\theta}}{\arg\min}\
-\sum_i \log\left(
p_{\mathbf{x}|\text{y}}(\boldsymbol{x}^{(i)}|y^{(i)};\boldsymbol{\mu}_y,\Sigma_y)
p_{\text{y}}(y^{(i)})
\right)\\
&=\underset{\boldsymbol{\theta}}{\arg\min}\
-\sum_i
\log\left(p_{\mathbf{x}|\text{y}}(\boldsymbol{x}^{(i)}|y^{(i)};\boldsymbol{\mu}_y,\Sigma_y)\right)
+\log\left(p_{\text{y}}(y^{(i)})\right)
\\
&=\underset{\boldsymbol{\theta}}{\arg\min}\
-\sum_i \log\left(p_{\mathbf{x}|\text{y}}(\boldsymbol{x}^{(i)}|y^{(i)};\boldsymbol{\mu}_y,\Sigma_y)\right)\\
\end{aligned} θ ^ MLE = θ arg min − log L ( θ ; D ) = θ arg min − i ∑ log ( p x ∣ y ( x ( i ) ∣ y ( i ) ; μ y , Σ y ) p y ( y ( i ) ) ) = θ arg min − i ∑ log ( p x ∣ y ( x ( i ) ∣ y ( i ) ; μ y , Σ y ) ) + log ( p y ( y ( i ) ) ) = θ arg min − i ∑ log ( p x ∣ y ( x ( i ) ∣ y ( i ) ; μ y , Σ y ) ) בהינתן ש-p y p_\text{y} p y
Quadratic Discriminant Analysis (QDA)
θ ^ MLE = arg min θ − ∑ i log ( p x ∣ y ( x ( i ) ∣ y ( i ) ; μ y , Σ y ) ) \hat{\boldsymbol{\theta}}_{\text{MLE}}
=\underset{\boldsymbol{\theta}}{\arg\min}\
-\sum_i \log\left(p_{\mathbf{x}|\text{y}}(\boldsymbol{x}^{(i)}|y^{(i)};\boldsymbol{\mu}_y,\Sigma_y)\right) θ ^ MLE = θ arg min − i ∑ log ( p x ∣ y ( x ( i ) ∣ y ( i ) ; μ y , Σ y ) )
נחלק את הסכימה לסכימות נפרדות על כל אחת מהמחלקות.
Quadratic Discriminant Analysis (QDA)
θ ^ MLE = arg min θ − ∑ i ∈ I 1 log ( p x ∣ y ( x ( i ) ∣ 1 ; μ 1 , Σ 1 ) ) − ∑ i ∈ I 2 log ( p x ∣ y ( x ( i ) ∣ 2 ; μ 2 , Σ 2 ) ) − … \begin{aligned}
\hat{\boldsymbol{\theta}}_{\text{MLE}}
=\underset{\boldsymbol{\theta}}{\arg\min}\
&-\sum_{i\in\mathcal{I}_1} \log\left(p_{\mathbf{x}|\text{y}}(\boldsymbol{x}^{(i)}|1;\boldsymbol{\mu}_1,\Sigma_1)\right) \\
&-\sum_{i\in\mathcal{I}_2} \log\left(p_{\mathbf{x}|\text{y}}(\boldsymbol{x}^{(i)}|2;\boldsymbol{\mu}_2,\Sigma_2)\right)
-\dots
\end{aligned} θ ^ MLE = θ arg min − i ∈ I 1 ∑ log ( p x ∣ y ( x ( i ) ∣ 1 ; μ 1 , Σ 1 ) ) − i ∈ I 2 ∑ log ( p x ∣ y ( x ( i ) ∣ 2 ; μ 2 , Σ 2 ) ) − …
Quadratic Discriminant Analysis (QDA)
עבור המחלקה ה c c c
μ ^ c , MLE , Σ ^ c , MLE = arg min μ c , Σ c − ∑ i ∈ I c log ( p x ∣ y ( x ( i ) ∣ c ; μ c , Σ c ) ) = arg min μ c , Σ c ∑ i ∈ I c log ( ∣ Σ c ∣ ) ) + 1 2 ( x ( i ) − μ c ) ⊤ Σ c − 1 ( x ( i ) − μ c ) \begin{aligned}
\hat{\boldsymbol{\mu}}_{c,\text{MLE}},\hat{\Sigma}_{c,\text{MLE}}
&=\underset{\boldsymbol{\mu}_c,\Sigma_c}{\arg\min}\
-\sum_{i\in\mathcal{I}_c} \log\left(p_{\mathbf{x}|\text{y}}(\boldsymbol{x}^{(i)}|c;\boldsymbol{\mu}_c,\Sigma_c)\right)\\
&=\underset{\boldsymbol{\mu}_c,\Sigma_c}{\arg\min}\
\sum_{i\in\mathcal{I}_c}
\log\left(\sqrt{|\Sigma_c|})\right)+
\frac{1}{2}(\boldsymbol{x}^{(i)}-\boldsymbol{\mu}_c)^{\top}\Sigma_c^{-1}(\boldsymbol{x}^{(i)}-\boldsymbol{\mu}_c)\\
\end{aligned} μ ^ c , MLE , Σ ^ c , MLE = μ c , Σ c arg min − i ∈ I c ∑ log ( p x ∣ y ( x ( i ) ∣ c ; μ c , Σ c ) ) = μ c , Σ c arg min i ∈ I c ∑ log ( ∣ Σ c ∣ ) ) + 2 1 ( x ( i ) − μ c ) ⊤ Σ c − 1 ( x ( i ) − μ c )
ניתן לפתור את הבעיה הזו על ידי גזירה והשוואה ל-0.
הפיתוח עבור Σ c \Sigma_c Σ c
Quadratic Discriminant Analysis (QDA)
החישוב של μ c \boldsymbol{\mu}_c μ c
f ( θ ; x ) = ∑ i ∈ I c log ( ∣ Σ c ∣ ) ) + 1 2 ( x ( i ) − μ c ) ⊤ Σ c − 1 ( x ( i ) − μ c ) f(\boldsymbol{\theta};\mathcal{x})
=\sum_{i\in\mathcal{I}_c}
\log\left(\sqrt{|\Sigma_c|})\right)+
\frac{1}{2}(\boldsymbol{x}^{(i)}-\boldsymbol{\mu}_c)^{\top}\Sigma_c^{-1}(\boldsymbol{x}^{(i)}-\boldsymbol{\mu}_c) f ( θ ; x ) = i ∈ I c ∑ log ( ∣ Σ c ∣ ) ) + 2 1 ( x ( i ) − μ c ) ⊤ Σ c − 1 ( x ( i ) − μ c ) ∂ f ∂ μ c = 0 ⇔ − ∑ i ∈ I c Σ c − 1 ( x ( i ) − μ c ) = 0 ⇔ ∣ I c ∣ μ c − ∑ i ∈ I c x ( i ) = 0 ⇔ μ c = 1 ∣ I c ∣ ∑ i ∈ I c x ( i ) \begin{aligned}
\frac{\partial f}{\partial\boldsymbol{\mu}_c}&=0\\
\Leftrightarrow-\sum_{i\in\mathcal{I}_c}\Sigma_c^{-1}(\boldsymbol{x}^{(i)}-\boldsymbol{\mu}_c)&=0\\
\Leftrightarrow|\mathcal{I}_c|\boldsymbol{\mu}_c-\sum_{i\in\mathcal{I}_c}\boldsymbol{x}^{(i)}&=0\\
\Leftrightarrow\boldsymbol{\mu}_c&=\frac{1}{|\mathcal{I}_c|}\sum_{i\in\mathcal{I}_c}\boldsymbol{x}^{(i)}\\
\end{aligned} ∂ μ c ∂ f ⇔ − i ∈ I c ∑ Σ c − 1 ( x ( i ) − μ c ) ⇔ ∣ I c ∣ μ c − i ∈ I c ∑ x ( i ) ⇔ μ c = 0 = 0 = 0 = ∣ I c ∣ 1 i ∈ I c ∑ x ( i )
Quadratic Discriminant Analysis (QDA)
הפרמטרים של המודל יהיו:
p y ( c ) = ∣ I c ∣ N p_{\text{y}}(c)=\frac{|\mathcal{I}_c|}{N} p y ( c ) = N ∣ I c ∣ μ c = 1 ∣ I c ∣ ∑ i ∈ I c x ( i ) \boldsymbol{\mu}_c=\frac{1}{|\mathcal{I}_c|}\sum_{i\in\mathcal{I}_c}\boldsymbol{x}^{(i)} μ c = ∣ I c ∣ 1 i ∈ I c ∑ x ( i ) Σ c = 1 ∣ I c ∣ ∑ i ∈ I c ( x ( i ) − μ c ) ( x ( i ) − μ c ) T \Sigma_c = \frac{1}{|\mathcal{I}_c|}\sum_{i\in\mathcal{I}_c}\left(\boldsymbol{x}^{(i)}-\boldsymbol{\mu}_c\right)\left(\boldsymbol{x}^{(i)}-\boldsymbol{\mu}_c\right)^T Σ c = ∣ I c ∣ 1 i ∈ I c ∑ ( x ( i ) − μ c ) ( x ( i ) − μ c ) T הצגנו כאן משערך אינטואיטבי להסתברות השיוך לכל מחלקה. אפשר להראות שזו התוצאה המתקבלת גם מהנחת מודל פילוג מולטינומיאלי למשתנה הקטגורי של המחלקה.
Quadratic Discriminant Analysis (QDA)
עבור פונקציית מחיר של סיכוי הטעות, החזאי האופטימאלי יהיה:
y ^ = h ( x ) = arg max y p x ∣ y ( x ∣ y ; μ y , Σ y ) p y ( y ) = arg max y − 1 2 ( x − μ y ) ⊤ Σ y − 1 ( x − μ y ) + log ( p y ( y ) ) ∣ Σ y ∣ ) \begin{aligned}
\hat{y}=h(\boldsymbol{x})
&=\underset{y}{\arg\max}\
p_{\mathbf{x}|\text{y}}(\boldsymbol{x}|y;\boldsymbol{\mu}_y,\Sigma_y)
p_{\text{y}}(y)\\
&=\underset{y}{\arg\max}\
-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu}_y)^{\top}\Sigma_y^{-1}(\boldsymbol{x}-\boldsymbol{\mu}_y)
+\log\left(\frac{p_{\text{y}}(y))}{\sqrt{|\Sigma_y|}}\right)\\
\end{aligned} y ^ = h ( x ) = y arg max p x ∣ y ( x ∣ y ; μ y , Σ y ) p y ( y ) = y arg max − 2 1 ( x − μ y ) ⊤ Σ y − 1 ( x − μ y ) + log ( ∣ Σ y ∣ p y ( y ) ) )
המקרה הבינארי - משטח הפרדה ריבועי
עבור המקרה של סיווג בינארי (סיווג לשתי מחלקות) מתקבל החזאי הבא:
h ( x ) = { 1 x T C x + a T x + b > 0 0 otherwise h\left(x\right)
=\begin{cases}
1\qquad \boldsymbol{x}^T C \boldsymbol{x} + \boldsymbol{a}^T \boldsymbol{x} + b > 0 \\
0\qquad \text{otherwise}\\
\end{cases} h ( x ) = { 1 x T C x + a T x + b > 0 0 otherwise כאשר:
C = 1 2 ( Σ 0 − 1 − Σ 1 − 1 ) C=\frac{1}{2}(\Sigma^{-1}_0-\Sigma^{-1}_1) C = 2 1 ( Σ 0 − 1 − Σ 1 − 1 ) a = Σ 1 − 1 μ 1 − Σ 0 − 1 μ 0 \boldsymbol{a}=\Sigma_{1}^{-1}\boldsymbol{\mu}_1-\Sigma^{-1}_0\boldsymbol{\mu}_0 a = Σ 1 − 1 μ 1 − Σ 0 − 1 μ 0 b = 1 2 ( μ 0 T Σ 0 − 1 μ 0 − μ 1 T Σ 1 − 1 μ 1 ) + log ( ∣ Σ 0 ∣ p y ( 1 ) ∣ Σ 1 ∣ p y ( 0 ) ) b=\tfrac{1}{2}\left(\boldsymbol{\mu}_0^T\Sigma_0^{-1}\boldsymbol{\mu}_0 - \boldsymbol{\mu}_1^T\Sigma_1^{-1}\boldsymbol{\mu}_1\right) + \log\left(\frac{\sqrt{|\Sigma_0|}p_\text{y}(1)}{\sqrt{|\Sigma_1|}p_\text{y}(0)}\right) b = 2 1 ( μ 0 T Σ 0 − 1 μ 0 − μ 1 T Σ 1 − 1 μ 1 ) + log ( ∣ Σ 1 ∣ p y ( 0 ) ∣ Σ 0 ∣ p y ( 1 ) ) התנאי שקיבלנו x T C x + a T x + b > 0 \boldsymbol{x}^T C \boldsymbol{x} + \boldsymbol{a}^T \boldsymbol{x} + b > 0 x T C x + a T x + b > 0 x \boldsymbol{x} x
Linear Discriminant Analysis (LDA)
p x ∣ y ( x ∣ c ; μ c , Σ ) = 1 ( 2 π ) D ∣ Σ ∣ exp ( − 1 2 ( x − μ c ) ⊤ Σ − 1 ( x − μ c ) ) p_{\mathbf{x}|\text{y}}(\boldsymbol{x}|c;\boldsymbol{\mu}_c,\Sigma)=
\frac{1}{\sqrt{(2\pi)^D|\Sigma|}}
\exp\left(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu}_c)^{\top}\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu}_c)\right) p x ∣ y ( x ∣ c ; μ c , Σ ) = ( 2 π ) D ∣ Σ ∣ 1 exp ( − 2 1 ( x − μ c ) ⊤ Σ − 1 ( x − μ c ) )
Linear Discriminant Analysis (LDA)
פתרון בעיית ה MLE:
p y ( c ) = ∣ I c ∣ N p_{\text{y}}(c)=\frac{|\mathcal{I}_c|}{N} p y ( c ) = N ∣ I c ∣ μ c = 1 ∣ I c ∣ ∑ i ∈ I c x ( i ) \boldsymbol{\mu}_c = \frac{1}{|\mathcal{I}_c|}\sum_{i\in \mathcal{I}_c}\boldsymbol{x}^{(i)} μ c = ∣ I c ∣ 1 i ∈ I c ∑ x ( i ) Σ = 1 N ∑ i ( x ( i ) − μ y ( i ) ) ( x ( i ) − μ y ( i ) ) T \Sigma = \frac{1}{N}\sum_{i}\left(\boldsymbol{x}^{(i)}-\boldsymbol{\mu}_{y^{(i)}}\right)\left(\boldsymbol{x}^{(i)}-\boldsymbol{\mu}_{y^{(i)}}\right)^T Σ = N 1 i ∑ ( x ( i ) − μ y ( i ) ) ( x ( i ) − μ y ( i ) ) T
Linear Discriminant Analysis (LDA)
עבור פונקציית מחיר של miscalssification rate, החזאי האופטימאלי המתקבל ממודל זה הינו:
y ^ = h ( x ) = arg max y p x ∣ y ( x ∣ y ; μ c , Σ ) p y ( y ) = arg max y − 1 2 ( x − μ y ) ⊤ Σ − 1 ( x − μ y ) + log ( p y ( y ) ) = arg min y x ⊤ Σ − 1 μ y − 1 2 μ y ⊤ Σ − 1 μ y − log ( p y ( y ) ) \begin{aligned}
\hat{y}=h(\boldsymbol{x})
&=\underset{y}{\arg\max}\
p_{\mathbf{x}|\text{y}}(\boldsymbol{x}|y;\boldsymbol{\mu}_c,\Sigma)
p_{\text{y}}(y)\\
&=\underset{y}{\arg\max}\
-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu}_y)^{\top}\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu}_y)
+\log(p_{\text{y}}(y))\\
&=\underset{y}{\arg\min}\
\boldsymbol{x}^{\top}\Sigma^{-1}\boldsymbol{\mu}_y
-\frac{1}{2}\boldsymbol{\mu}_y^{\top}\Sigma^{-1}\boldsymbol{\mu}_y
-\log(p_{\text{y}}(y))\\
\end{aligned} y ^ = h ( x ) = y arg max p x ∣ y ( x ∣ y ; μ c , Σ ) p y ( y ) = y arg max − 2 1 ( x − μ y ) ⊤ Σ − 1 ( x − μ y ) + log ( p y ( y ) ) = y arg min x ⊤ Σ − 1 μ y − 2 1 μ y ⊤ Σ − 1 μ y − log ( p y ( y ) )
המקרה הבינארי
עבור המקרה של סיווג בינארי (סיווג לשני מחלקות) מתקבל החזאי הבא:
h ( x ) = { 1 a T x + b > 0 0 otherwise h\left(x\right)
=\begin{cases}
1\qquad \boldsymbol{a}^T \boldsymbol{x} + b > 0 \\
0\qquad \text{otherwise}\\
\end{cases} h ( x ) = { 1 a T x + b > 0 0 otherwise כאשר:
a = Σ − 1 ( μ 1 − μ 0 ) \boldsymbol{a}=\Sigma^{-1}\left(\boldsymbol{\mu}_1-\boldsymbol{\mu}_0\right) a = Σ − 1 ( μ 1 − μ 0 ) b = 1 2 ( μ 0 T Σ − 1 μ 0 − μ 1 T Σ − 1 μ 1 ) + log ( p y ( 1 ) p y ( 0 ) ) b=\tfrac{1}{2}\left(\boldsymbol{\mu}_0^T\Sigma^{-1}\boldsymbol{\mu}_0 - \boldsymbol{\mu}_1^T\Sigma^{-1}\boldsymbol{\mu}_1\right) + \log\left(\frac{p_\text{y}\left(1\right)}{p_\text{y}\left(0\right)}\right) b = 2 1 ( μ 0 T Σ − 1 μ 0 − μ 1 T Σ − 1 μ 1 ) + log ( p y ( 0 ) p y ( 1 ) ) התנאי שקיבלנו a T x + b > 0 \boldsymbol{a}^T \boldsymbol{x} + b > 0 a T x + b > 0 x \boldsymbol{x} x
המקרה הכללי (לא בינארי)
במקרה הכללי המרחב יהיה מחולק ל C C C
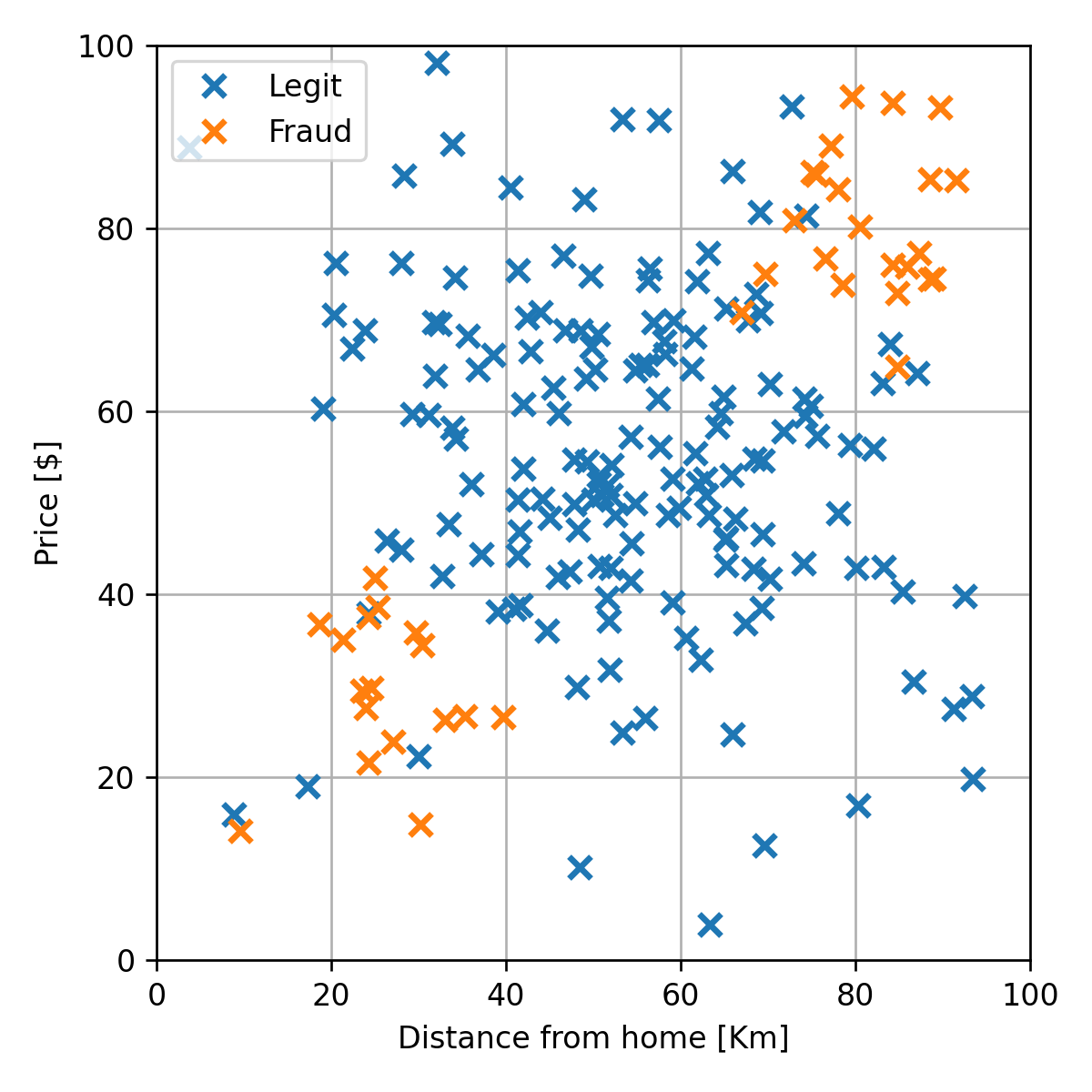
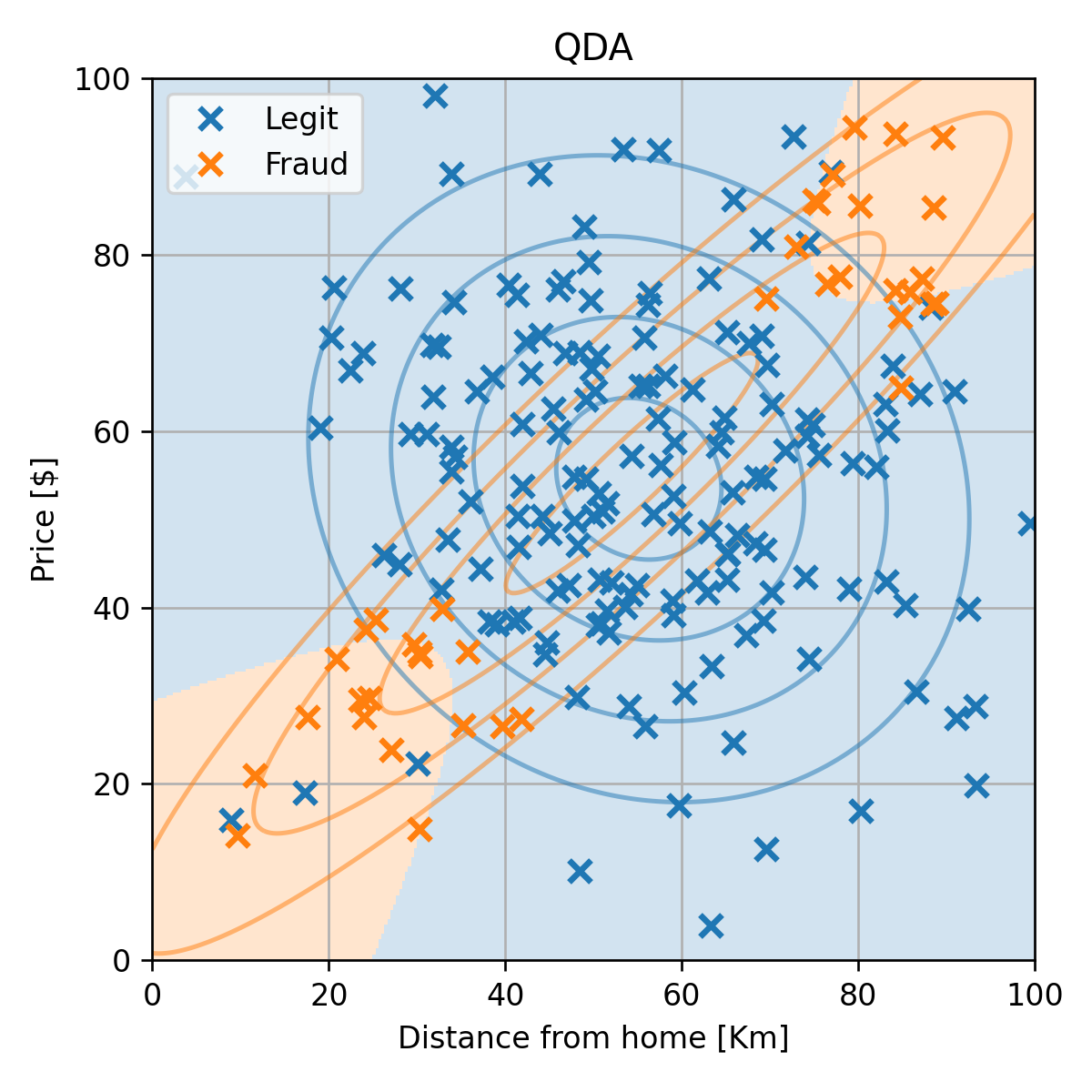
דוגמא
נסתכל שוב על הבעיה של חיזוי עסקאות שחשודות כהונאות:
התאמה של מודל QDA
p y ( 0 ) = ∣ I 0 ∣ N = 0.81 p_{\text{y}}(0)=\frac{|\mathcal{I}_0|}{N}=0.81 p y ( 0 ) = N ∣ I 0 ∣ = 0 . 8 1 p y ( 1 ) = ∣ I 1 ∣ N = 0.19 p_{\text{y}}(1)=\frac{|\mathcal{I}_1|}{N}=0.19 p y ( 1 ) = N ∣ I 1 ∣ = 0 . 1 9 μ 0 = 1 ∣ I 0 ∣ ∑ i ∈ I 0 x ( i ) = [ 55.1 , 54.6 ] ⊤ \boldsymbol{\mu}_0 = \frac{1}{|\mathcal{I}_0|}\sum_{i\in \mathcal{I}_0}\boldsymbol{x}^{(i)}=[55.1,54.6]^{\top} μ 0 = ∣ I 0 ∣ 1 i ∈ I 0 ∑ x ( i ) = [ 5 5 . 1 , 5 4 . 6 ] ⊤ μ 1 = 1 ∣ I 1 ∣ ∑ i ∈ I 1 x ( i ) = [ 54.4 , 55.2 ] ⊤ \boldsymbol{\mu}_1 = \frac{1}{|\mathcal{I}_1|}\sum_{i\in \mathcal{I}_1}\boldsymbol{x}^{(i)}=[54.4,55.2]^{\top} μ 1 = ∣ I 1 ∣ 1 i ∈ I 1 ∑ x ( i ) = [ 5 4 . 4 , 5 5 . 2 ] ⊤ Σ 0 = 1 ∣ I 0 ∣ ∑ i ( x ( i ) − μ y ( i ) ) ( x ( i ) − μ y ( i ) ) T = [ 350.9 − 42.9 − 42.9 336 ] \Sigma_0 = \frac{1}{|\mathcal{I}_0|}\sum_{i}\left(\boldsymbol{x}^{(i)}-\boldsymbol{\mu}_{y^{(i)}}\right)\left(\boldsymbol{x}^{(i)}-\boldsymbol{\mu}_{y^{(i)}}\right)^T
=\begin{bmatrix}
350.9 & -42.9 \\
-42.9 & 336
\end{bmatrix} Σ 0 = ∣ I 0 ∣ 1 i ∑ ( x ( i ) − μ y ( i ) ) ( x ( i ) − μ y ( i ) ) T = [ 3 5 0 . 9 − 4 2 . 9 − 4 2 . 9 3 3 6 ] Σ 1 = 1 ∣ I 1 ∣ ∑ i ( x ( i ) − μ y ( i ) ) ( x ( i ) − μ y ( i ) ) T = [ 817.9 730.5 730.5 741.7 ] \Sigma_1 = \frac{1}{|\mathcal{I}_1|}\sum_{i}\left(\boldsymbol{x}^{(i)}-\boldsymbol{\mu}_{y^{(i)}}\right)\left(\boldsymbol{x}^{(i)}-\boldsymbol{\mu}_{y^{(i)}}\right)^T
=\begin{bmatrix}
817.9 & 730.5 \\
730.5 & 741.7
\end{bmatrix} Σ 1 = ∣ I 1 ∣ 1 i ∑ ( x ( i ) − μ y ( i ) ) ( x ( i ) − μ y ( i ) ) T = [ 8 1 7 . 9 7 3 0 . 5 7 3 0 . 5 7 4 1 . 7 ]
התאמה של מודל QDA
שגיאת החיזוי (miscalssification rate) על ה test set הינה 0.08.
התוצאה סבירה, אך ניתן לראות שגאוסיאן לא מאד מתאים לפילוג של ההונאות.
הבעיה של הגישה הגנרטיבית הפרמטרית
הינו רוצים מודל אשר יכול לייצג בנפרד את שני האיזורים.
לצערינו המבחר של המודלים בהם אנו יכולים לא גדול.
המגבלה הזו נובעת מהצורך שהמודל ייצג פילוג חוקיים.
הערה : קיימות הרבה הרחבות שנידונות במקורסים מתקדמים יותר, למשל, תערובת של גאוסיאניים.
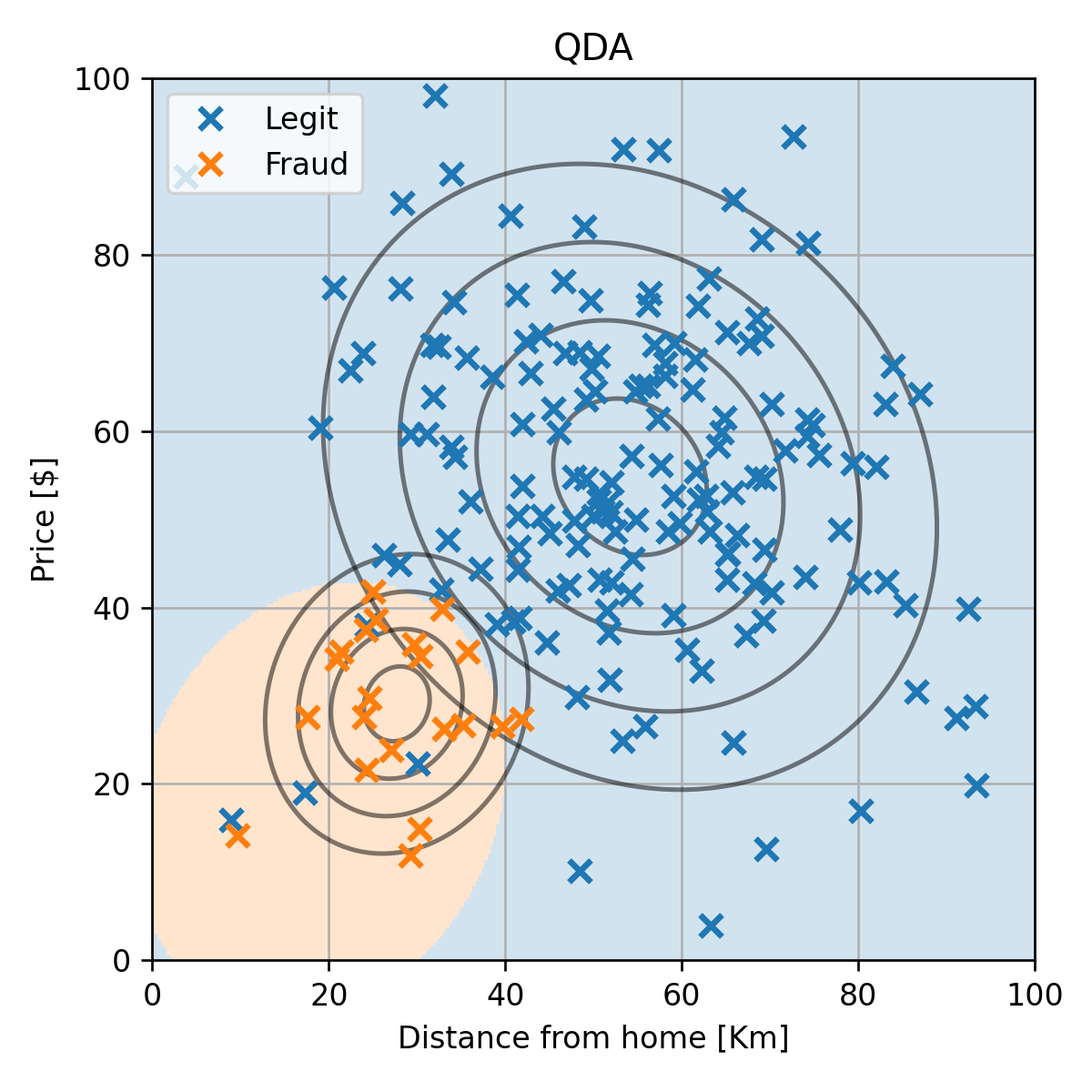
דוגמא למדגם שמתאים למודל של QDA
לצורך הדגמה נסתכל על גירסא של המדגם שבה יש רק איזור אחד של ההונאות:
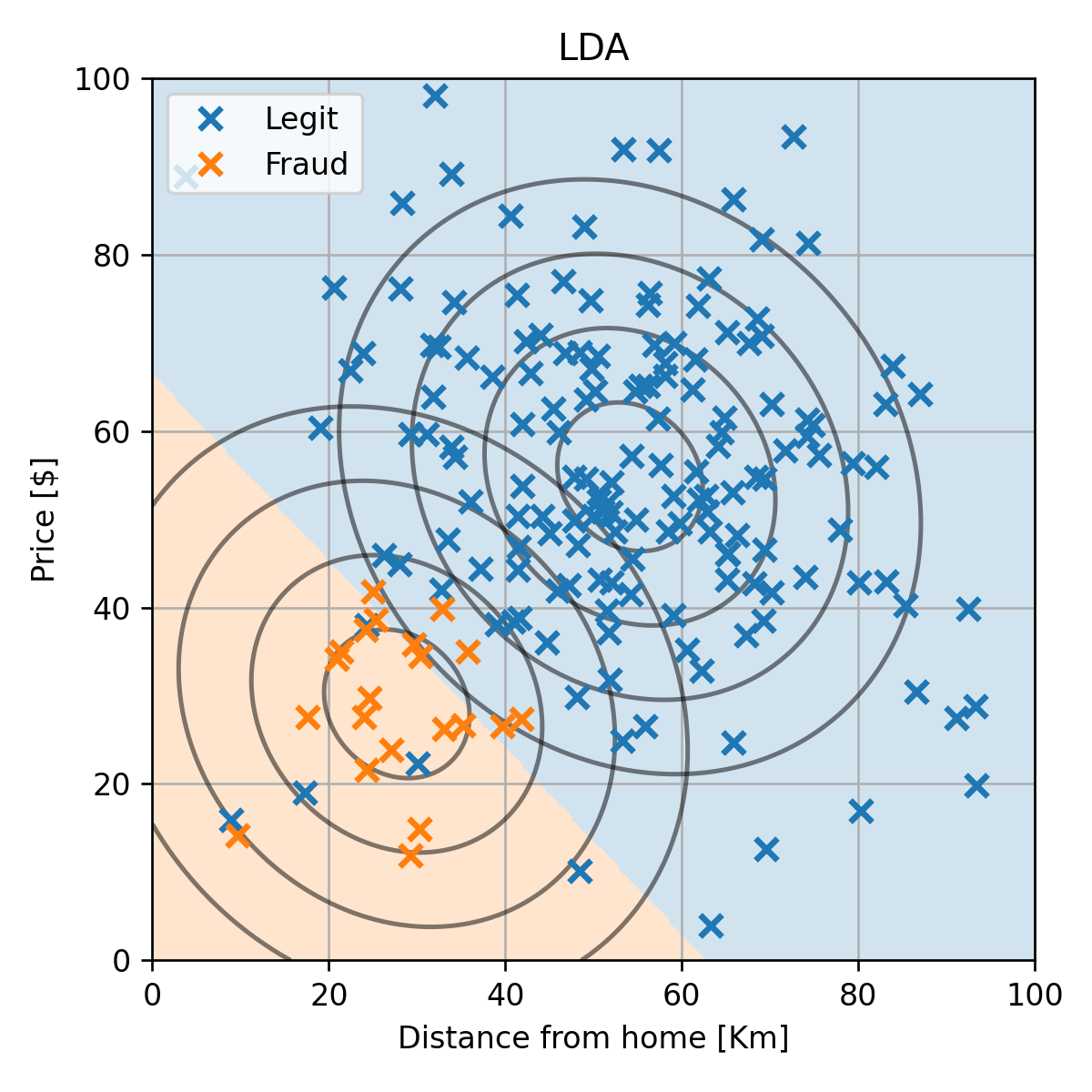
מודל LDA
נציג גם את התוצאה המתקבלת ממודל ה LDA: