הרצאה 7 - שיערוך פילוג בשיטות לא פרמטריות

מה נלמד היום

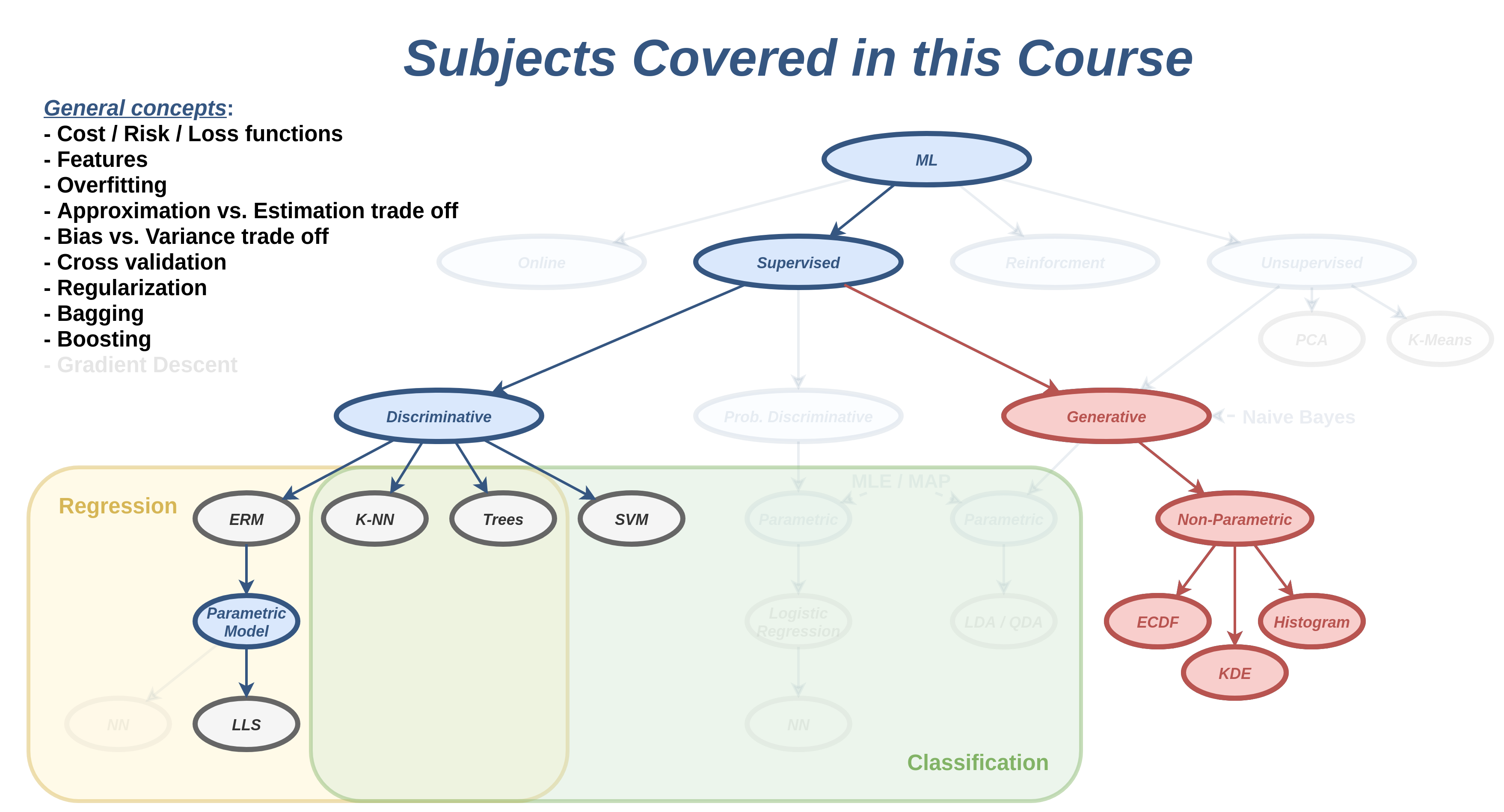
דיסקרימינטיבי vs. גנרטיבי

הגישה הדיסקרימינטיבית

הגישה הגנרטיבית

הקשר לבעיות unsupervised learning

• בקורס זה לא נעסוק כמעט בבעיות unsupervised learning.
• בבעיות unsupervised learning המדגם מכיל סוג אחד של משתנים $\mathbf{x}$.
• ננסה ללמוד מהם התכונות שמאפיינות את הדגימות במדגם.
• אחת הדרכים הטובות ביותר לעשות זאת היא על ידי שיערוך הפילוג שלהם.

שיערוך הפילוג

הבעיה של בניית מודל הסתברותי של משתנים אקראיים מתוך מדגם מכונה בעיית שיערוך (estimation). את המודל ההסתברותי אנו נבטא בעזרת אחת מהפונקציות הבאות:

• פונקציית ההסתברות (probablity mass function - PMF)
• פונקציית צפיפות ההסתברות (probability density function - PDF)
• פונקציית הפילוג המצרפית (cumulative distribution function CDF).

חיזוי (prediction) ושיערוך (estimation)

• בבעיות חיזוי אנו מועניינים לחזות את ערכו של משתנה אקראי, לרוב על סמך משתנה / וקטור אקראי בודד (דגימה יחידה).
• בבעיות שיערוך אנו מעוניינים לבנות מודל הסתברותי של משתנה / משתנים אקראיים לרוב על סמך הרבה דגימות.

דוגמא

נסתכל לדוגמא על המדגם של הונאות אשראי מהרצאה הקודמת:

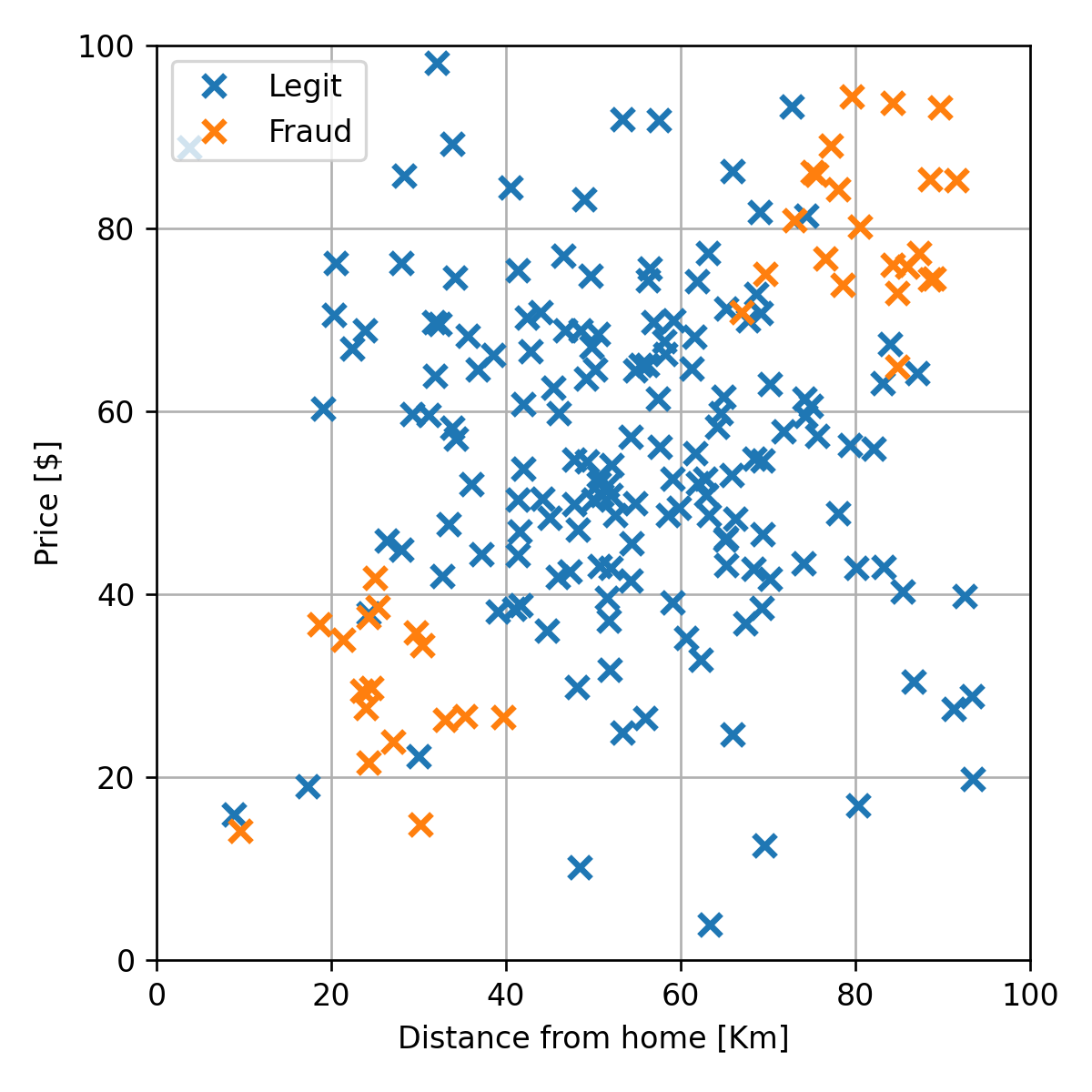
נרצה לשערך את הפילוג של המשתנים על פי מדגם זה

דוגמא

לדוגמא היינו רוצים למצוא פונקציות אשר יתארו את הפילוג של הדגימות החוקיות ושל ההונאות:

שיערוך א-פרמטריות

בהרצאה הקרובה נעסוק בשיטות שיערוך אשר מכונות שיטות לא פרמטריות או א-פרמטריות, מהות השם תהיה ברורה יותר אחרי שנציג בהרצאה הבאה את הנושא של שיטות פרמטריות.

שיערוך ההסתברות של מאורע

דוגמא

נניח שיש בידינו את המדגם הבא של מדידות של זמני נסיעה (בדקות) מחיפה לתל אביב על כביש החוף:

ברצונינו לשערך את ההסתברות של המאורע שנסיעה מסויימת תיקח פחות משעה, $A=\{x<60\}$.

שיערוך ההסתברות של מאורע

דוגמא

נשערך שהסתברות זו שווה למספר הפעמים היחסי שמאורע זה קרה במדגם הנתון:

• נשתמש בסימון "כובע" לציון גודל שאותו אנו חוזים / משערכים באופן אמפירי.
• נציין את העובדה שמשערך תלוי במדגם שבו השתמשנו על ידי הוספת $\mathcal{D}$ מתחת למשערך.

מדידה אמפירית (empirical measure)
/ משערך הצבה

בהינתן מדגם מסויים $\mathcal{D}=\{\boldsymbol{x}^{(i)}\}_{i=0}^N$, המדידה האמפירית, $\hat{p}_{A,\mathcal{D}}$, הינה שיערוך של הההסתברות, $Pr\left(A\right)$, והיא מחושבת באופן הבא:

נוכל כעת להשתמש בשיטה זו על מנת לנסות ולשערך את הפילוג של משתנים אקראיים.

משתנה אקראי דיסקרטי

דוגמא 1 - משתנה בינארי

• $\text{x}$ תוצאת הטלה של מטבע לא הוגן.
• הטלנו את המטבע 10 פעמים וקיבלנו:

מה ה PMF של $\text{x}$?

משתנה אקראי דיסקרטי

דוגמא 1 - משתנה בינארי

גם כאן נשערך את ההסתברויות של הערכים ש $\text{x}$ מקבל על פי השכיחות שלהם במדגם:

• זו למעשה מדידה אמפירית של המאורע ש $\{\text{x}=x\}$.

משתנה אקראי דיסקרטי

דוגמא 2 - משתנה לא בינארי

• $\text{x}$ תוצאת הטלה של קוביה לא הוגנת.
• הטלנו את הקוביה 10 פעמים וקיבלנו:

מה ה PMF של $\text{x}$?

משתנה אקראי דיסקרטי

דוגמא 2 - משתנה לא בינארי

בדיוק כמו קודם, נשערך את ההסתברות לקבל כל ערך לפי השכיחות שלו במדגם:

ניסוח פורמאלי

בהינתן מדגם מסויים $\mathcal{D}=\{\boldsymbol{x}^{(i)}\}_{i=0}^N$, נוכל לשערך את ה PMF של משתנה / וקטור אקראי דיסקרטי באופן הבא:

שימו לב שמובטח לנו שנקבל פונקציית הסתברות חוקית (חיובית שהסכום עליה שווה ל1).

שיערוך הפילוג המצרפי

נזכור כי פונקציית הפילוג המצרפי (ה CDF) מוגדרת באופן הבא:

נוכל אם כן לשערך גודל זה על ידי שימוש במדידה האמפירית בעבור המאורע של $A=\{\text{x}_j\leq {x}_j \, \forall j\}$ באופן הבא:

משערך זה נקרא empirical cumulative distribtuion function (ECDF).

ECDF - דוגמא

נשערך את הפילוג המצרפי של זמני הנסיעה בכביש החוף

ECDF - דוגמא

זוהי למעשה פונקציה קבועה למקוטעין אשר נראית כך:

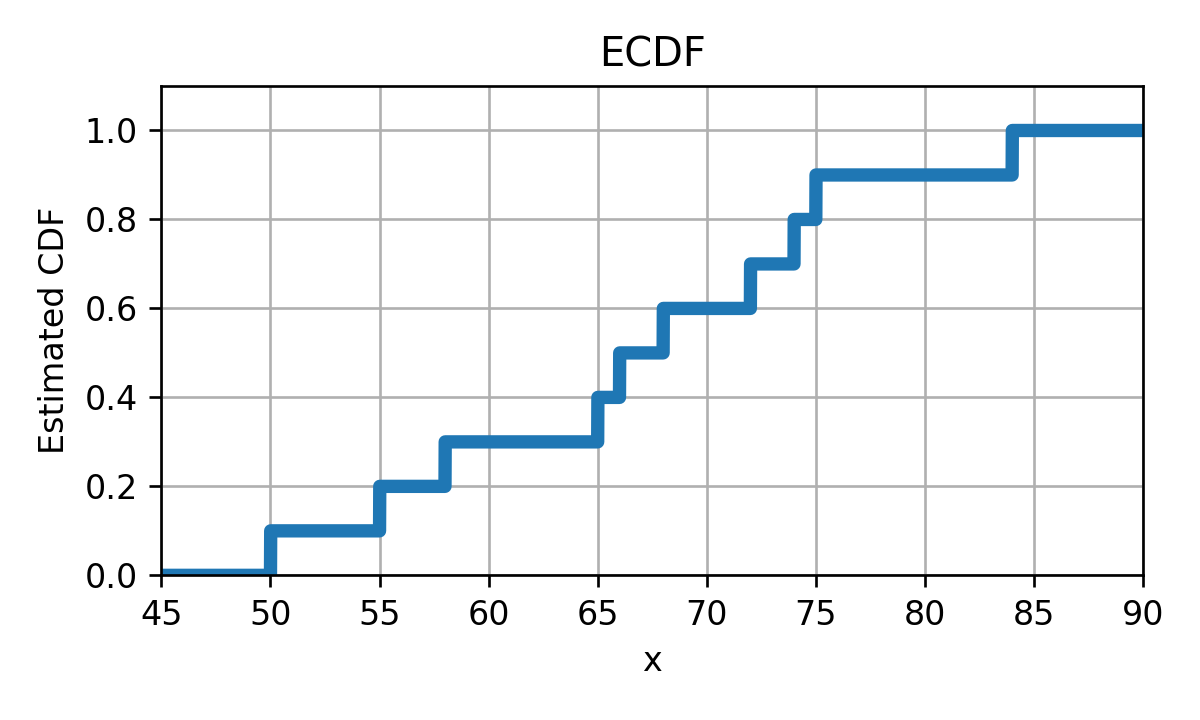
בעיה: איך נראה ה PDF?

ECDF - דוגמא

ככה:

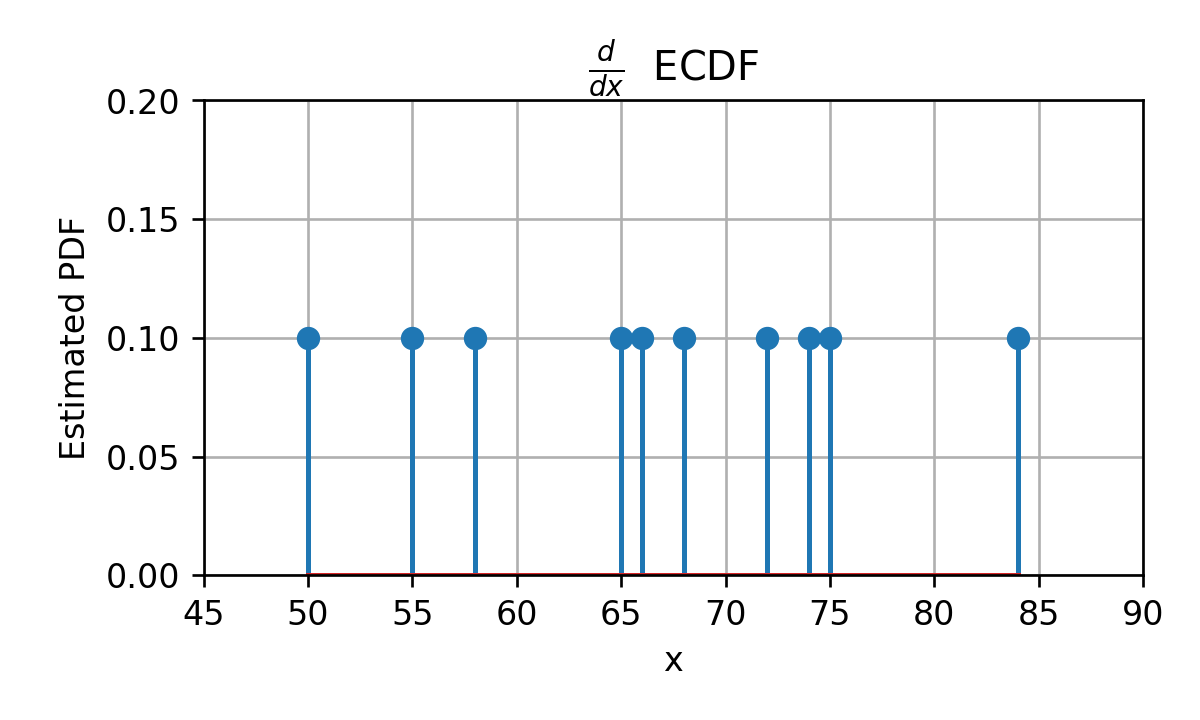
פונקציה כזו היא לא מאד שימושית.

היסטוגרמה

נסיון לשערך PDF על ידי קוונטיזציה של משתנה רציף.

• נחלק את טווח הערכים למספר סופי של חלקים המכוונים bins (תאים).
• נשתמש במדידה אמפירת על מנת לשערך את ההסתברות להימצא בכל תא.

היסטוגרמה - דוגמא

נחלק את התחום ל 5 קטעים:

ההסתברות להיות בכל bin הינה:

יש לבחור את ה bins כך שיכסו את התחום ולא יחפפו.

היסטוגרמה

בכדי להפוך את ההסתברויות לצפיפות הסתברות נרצה "למרוח" את ההסתברות שקיבלנו באופן אחיד על פני ה bin.

היסטוגרמה - דוגמא

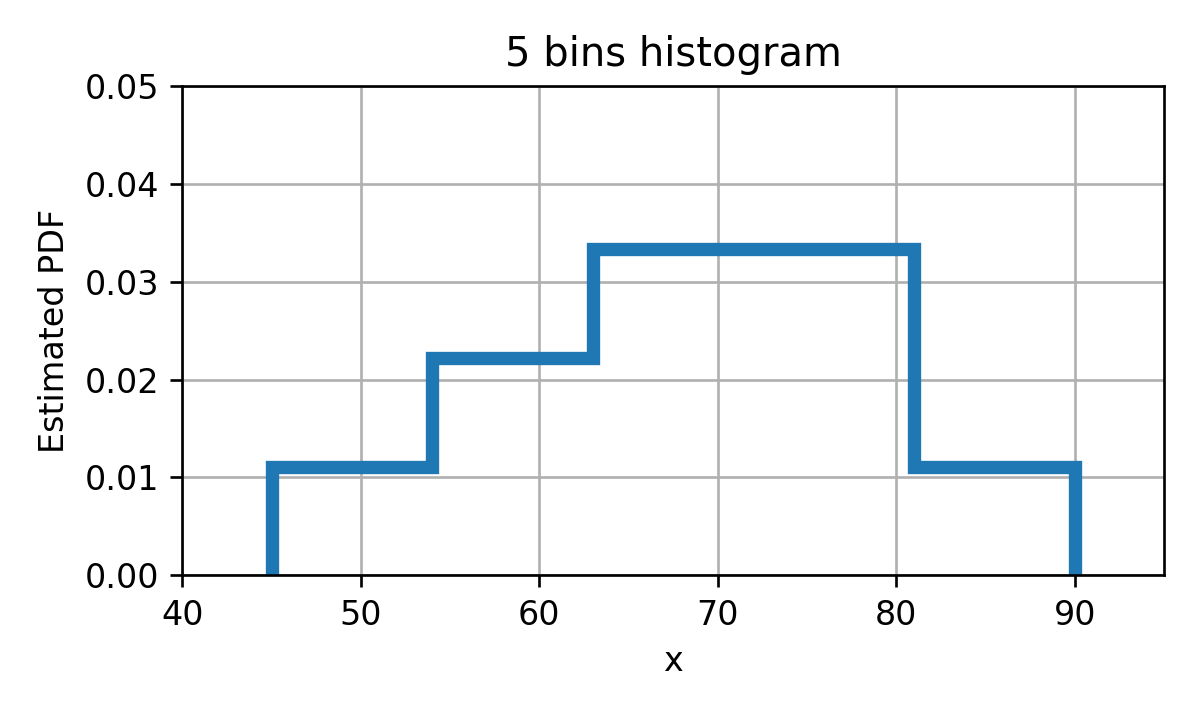
היסטוגרמה - ניסוח פורמאלי

בהינתן מדגם מסויים $\mathcal{D}=\{\boldsymbol{x}^{(i)}\}_{i=0}^N$, ההיסטוגרמה הינה שיערוך של ה PDF של משתנה / וקטור אקראי והיא מחושבת באופן הבא:

1. מחלקים את תחום הערכים ש $\mathbf{x}$ יכול לקבל ל bins (תאים) לא חופפים אשר מכסים את כל התחום.
2. לכל bin משערכים את ההסתברות של המאורע שבו $\mathbf{x}$ יהיה בתוך התא.
3. הערך של פונקציית הצפיפות בכל תא תהיה ההסתברות המשוערכת להיות בתא חלקי גודל התא.

לבחירת ה bins יש השפעה גדולה על איכות השיערוך שנקבל. ננסה להבין את השיקולים בבחירת ה bins.

היסטוגרמה - המקרה הסקלרי

• $B$ מספר התאים.
• $l_b$ ו $r_b$ את הגבול השמאלי והימני התא ה $b$.

Overfitting ו underfitting של היסטוגרמה

דוגמא - שני מקרים קיצוניים

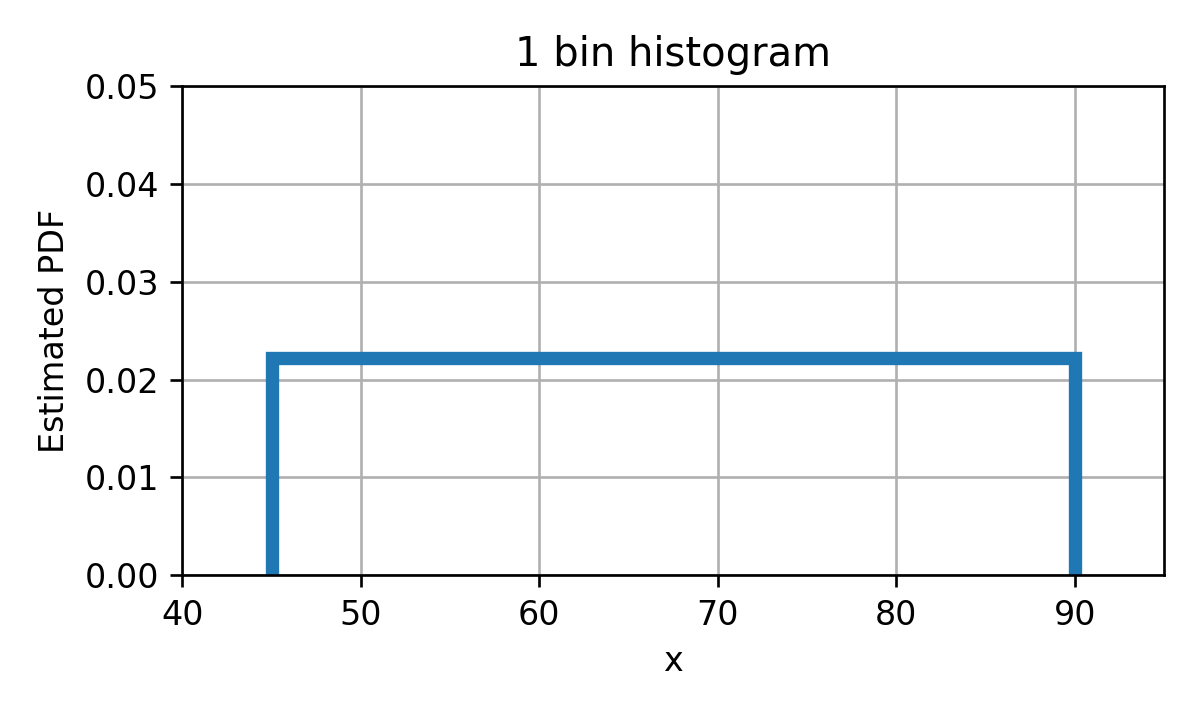
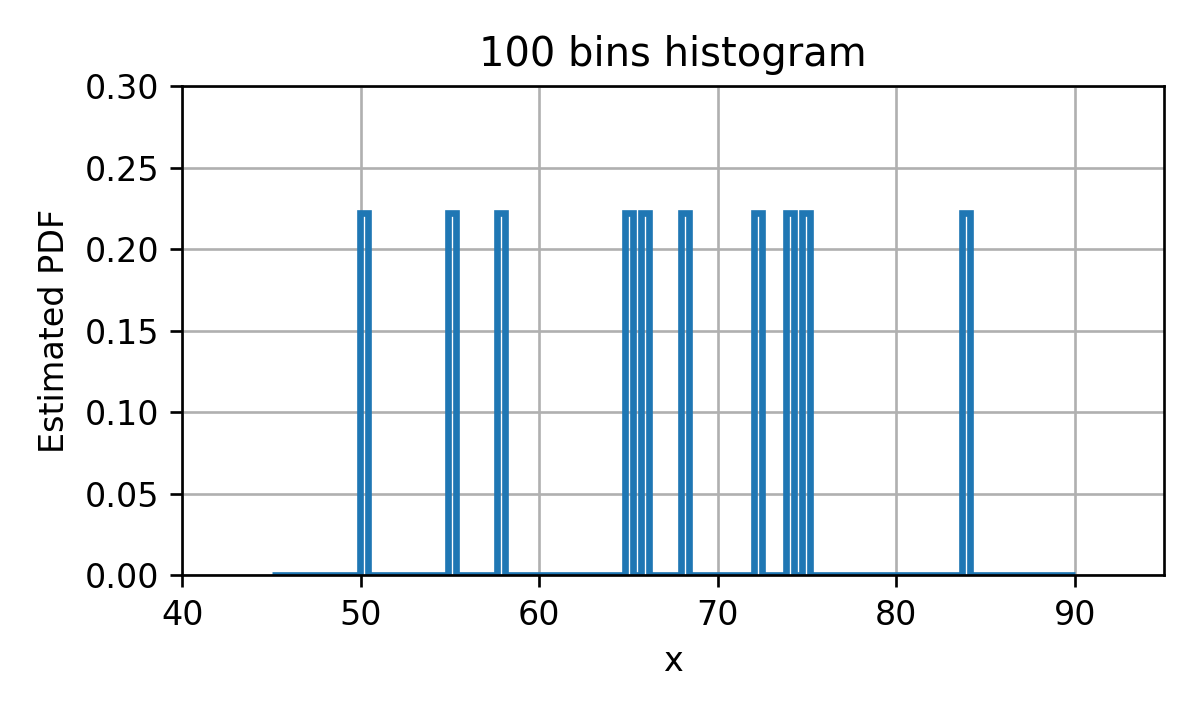
Overfitting ו underfitting של היסטוגרמה

מספר תאים קטן

Underfitting: יכולת מוגבלת לקרב את ה PDF האמיתי.

מספר תאים גדול

Overfitting: ההיסטוגרמה תתאר בצורה טובה את הדגימות אך לא את הפילוג האמיתי.

בחירת התאים

• מקובל לחלק ל $k$ תאים אחידים בגודלם.
• מכיוון שה $k$ האופטימאלי ישתנה מבעיה לבעיה, נאלץ לרוב לבחור אותו בעזרת ניסוי וטעיה.
• ישנם מספר כללי אצבע אשר במרבית המקרים יתנו תוצאה לא רעה.
• הכלל הנפוץ ביותר הינו לבחור את $k$ להיות שורש מספר הדגימות במדגם (מעוגל כלפי מעלה): $k=\left\lceil\sqrt{N}\right\rceil$

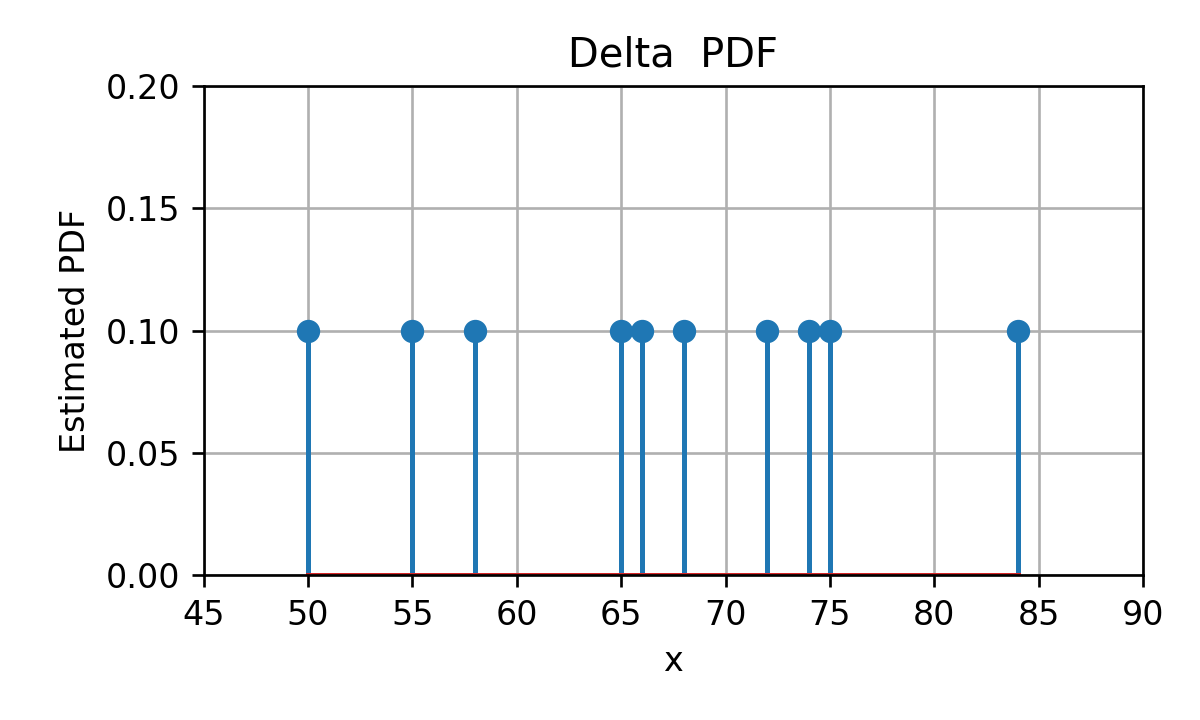
Kernel Density Estimation (KDE)

נתחיל מ PDF שבו אנו ממקמים פונקציית דלתא בגובה $\frac{1}{N}$ בכל נקודה אשר מופיעה במדגם.

לדוגמא, בעבור זמני הנסיעה בכביש החוף נקבל:

Kernel Density Estimation (KDE)

נחליף כל דלתא בפונקציית גרעין בעלת רוחב גדול מ-0.

לדוגמא גאוסיאנים:

Kernel Density Estimation (KDE)

נסכום את כל פונקציות הגרעין לקבלת ה PDF המשוערך:

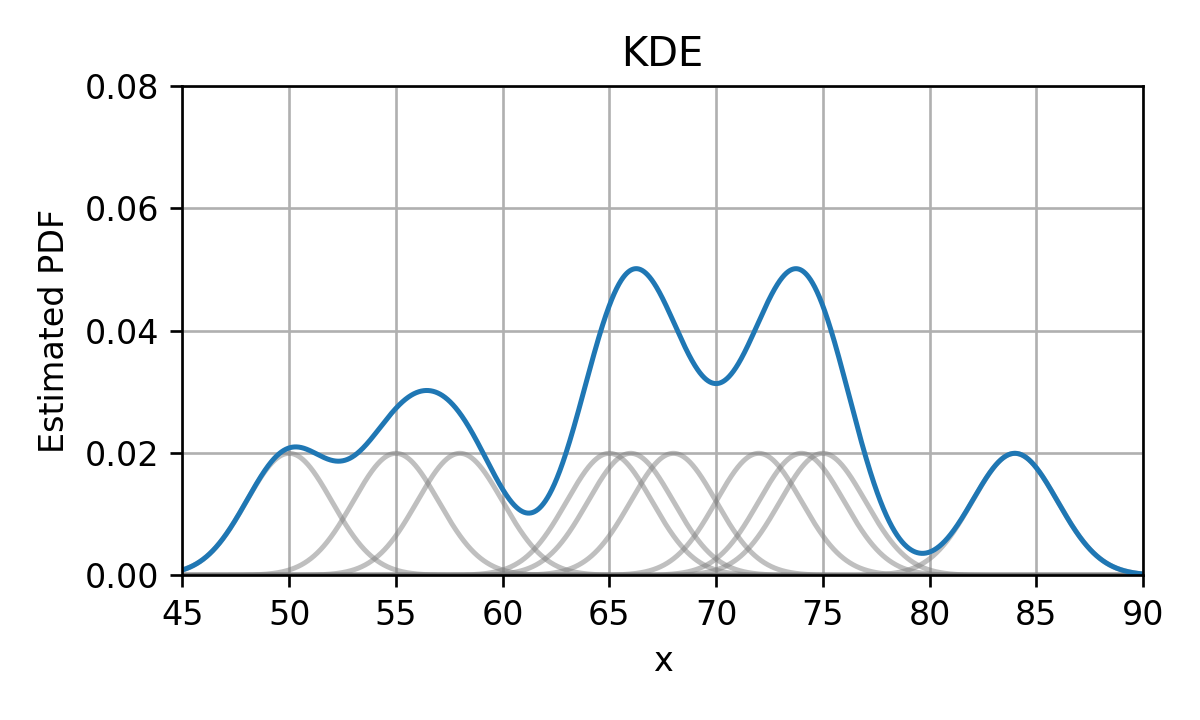
Kernel Density Estimation (KDE)

• פונקציות הגרעין (kernel) מכונות גם Parzen window.
• ומקובל לסמנם ב $\phi(\boldsymbol{x})$.

אם כן, משערך ה KDE נתון על ידי:

הערה: תנאי מספיק והכרחי בכדי שנקבל PDF חוקי, הינו שפונקציית הגרעיון תהיה בעצמה PDF חוקי.

בהקשר של עיבוד אותות: למעשה אנו מבצעים קונבולוציה בין פונקציית הדלתאות לבין פונקציית הגרעין. נרצה שהגרעין ישמש כמעיין low pass filter.

הוספת פרמטר רוחב

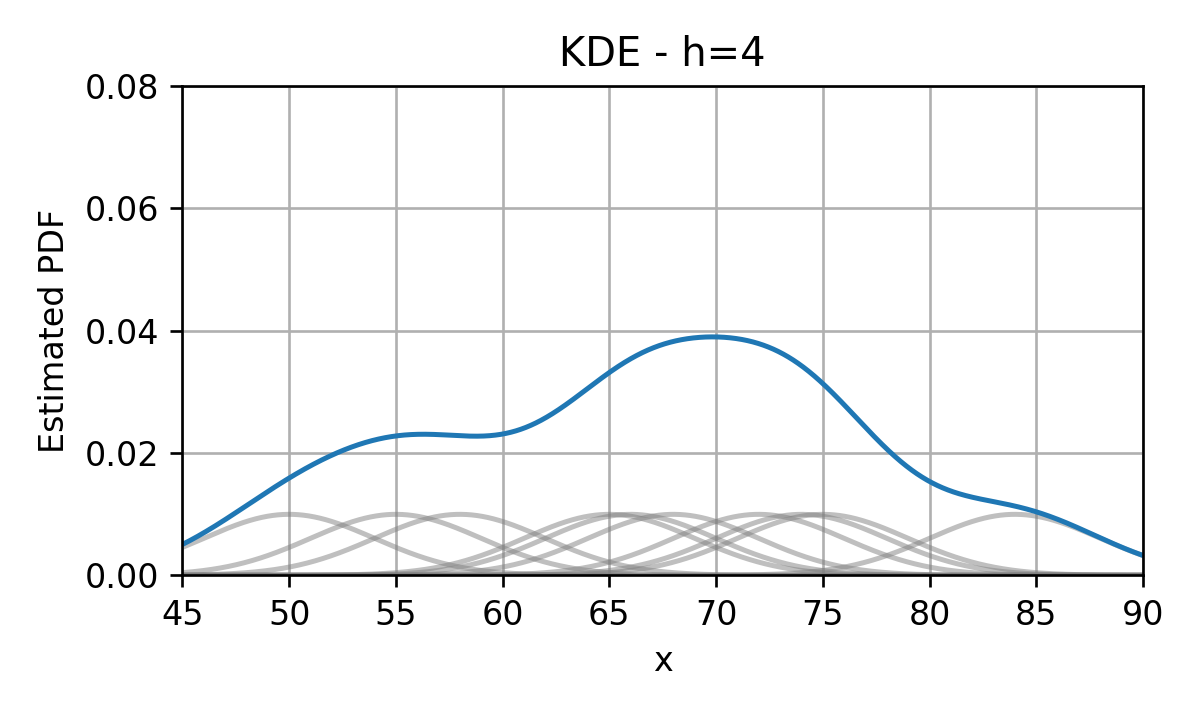
מקובל להוסיף פרמטר $h$ אשר שולט ברוחב של הגרעין:

בתוספת פרמטר זה המשערך יהיה:

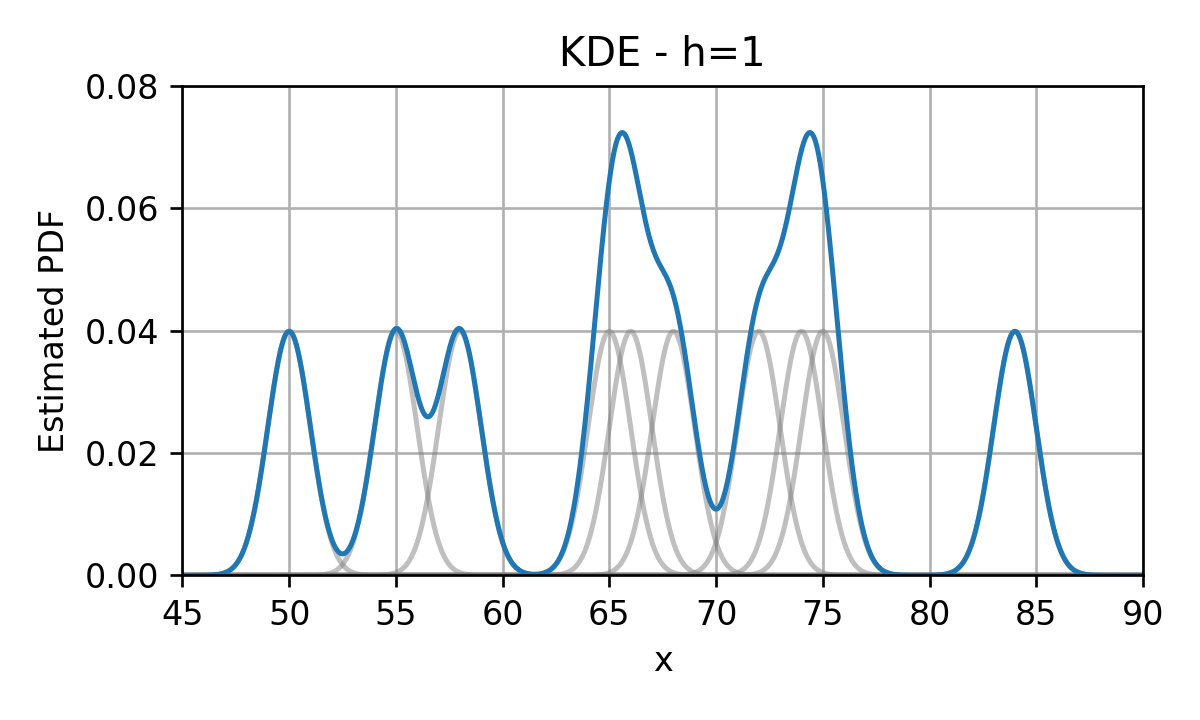
פונקציות גרעין נפוצות

שתי הבחירות הנפוצות ביותר לפונקציית הגרעין הינן:

1. חלון מרובע:

   $\phi_h(\boldsymbol{x})=\frac{1}{h^D}I\{|x_j|\leq \tfrac{h}{2}\quad\forall j\}$

כלל אצבע עבור חלון ריבועי: נבחר את גודל החלון אדפטיבית כך שיכלול $\sqrt{N}$ דגימות מסביב לנקודה הנחקרת.

2. גאוסיאן:

   $\phi_{\sigma}\left(x\right)=\frac{1}{\sqrt{2\pi}\sigma^D}\exp\left(-\frac{\lVert x\rVert_2^2}{2\sigma^2}\right)$

כלל אצבע לבחירת רוחב הגרעין במקרה הגאוסי הסקלרי:

$\sigma=\left(\frac{4\cdot\text{std}(\text{x})^5}{3N}\right)^\frac{1}{5}\approx1.06\ \text{std}(\text{x})N^{-\tfrac{1}{5}}$

שיערוך של פילוגים מעורבים

• נניח שאנו רוצים לשערך את הפילוג המשותף של $\text{x}$ ו $\text{y}$ כאשר $\text{x}$ הוא משתנה רציף ו $\text{y}$ הוא משתנה בדיד.
• במקרים כאלה נוח לפרק את פונקציית הפילוג המשותף באופן הבא:

ולהפריד את בעיית השיערוך לשני חלקים:

1. השיערוך של $p_{\text{y}}(y)$
2. השיערוך של $p_{\mathbf{x}|\text{y}}(\boldsymbol{x}|y)$ - כאן נשערך את הפילוג בנפרד לכל ערך של $\text{y}$.

שיערוך של פילוגים מעורבים - דוגמא

נחזור לדוגמא של הונאות האשראי:

שיערוך של פילוגים מעורבים - דוגמא

נתחיל בשיערוך של $\text{y}$.

• $\text{y}$ בדיד ולכן נוכל לשערך את ה PMF שלו על פי השכיחות של הערכים במדגם.
• מתוך ה 200 עסקאות ישנם 160 עסקאות חוקיות ו 40 עסקאות שחשודות כהונאה. לכן:

שיערוך של פילוגים מעורבים - דוגמא

נמשיך לשיערוך של $p_{\mathbf{x}|\text{y}}(\boldsymbol{x}|y)$.

• נשערך בנפרד את $p_{\mathbf{x}|\text{y}}(\boldsymbol{x}|0)$ ואת $p_{\mathbf{x}|\text{y}}(\boldsymbol{x}|1)$.

נתחיל מ $p_{\mathbf{x}|\text{y}}(\boldsymbol{x}|0)$. בשביל לשערך פילוג זה נסתכל רק על הדגימות השייכות של $\text{y}=0$:

שיערוך של פילוגים מעורבים - דוגמא

נשתמש ב KDE על מנת לשערך את $p_{\mathbf{x}|\text{y}}(\boldsymbol{x}|0)$:

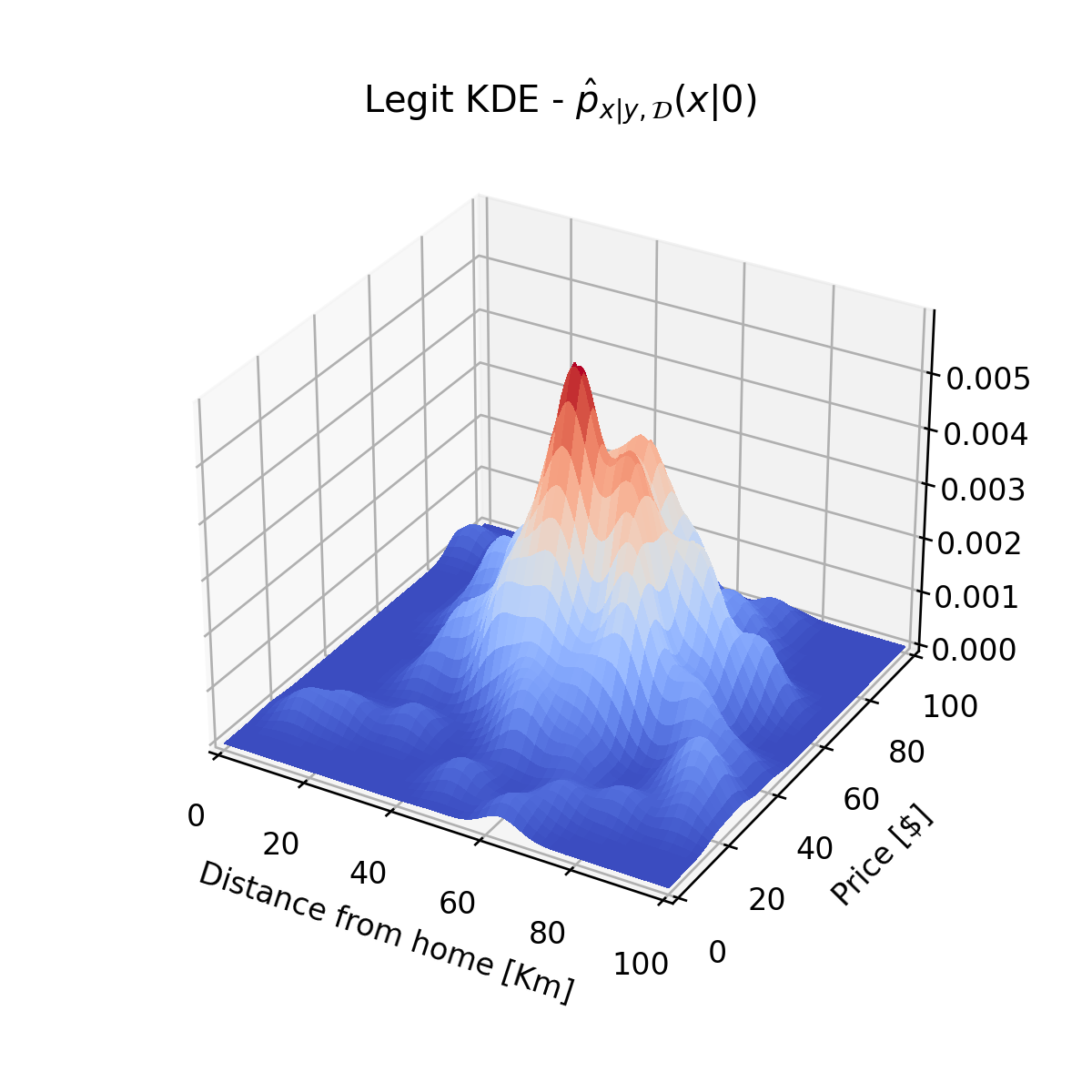
שיערוך של פילוגים מעורבים - דוגמא

באופן דומה נשערך גם את $p_{\mathbf{x}|\text{y}}(\boldsymbol{x}|1)$:

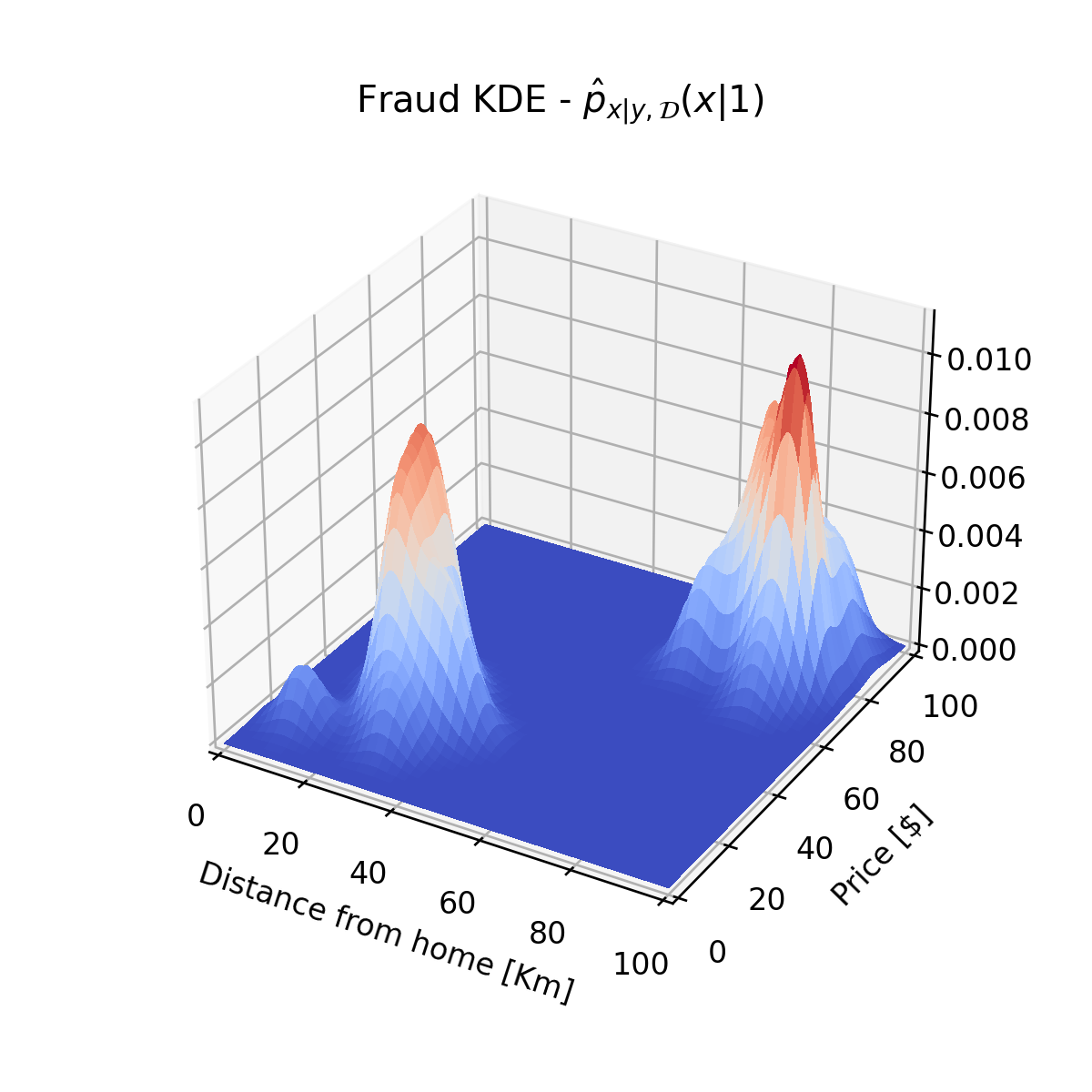
שיערוך של פילוגים מעורבים - דוגמא

שלושת הפילוגים ששיערכנו מרכיבים את הפילוג המשותף על פי:

שימוש בפילוג המשוערך לפתרון בעיות supervised learning

הגישה הגנרטיבית

עשינו את השלב הראשון, נעשה כעת את השלב השני.

חזאים אופטימאליים של פונקציות מחיר מוכרות - תזכורת

• MSE: התוחלת המותנית:

  $$h^*(\boldsymbol{x})=\mathbb{E}[y|x]$$

• MAE: החציון של הפילוג המותנה:

  $$h^*(\boldsymbol{x})=y_{\text{median}}\qquad \text{s.t.}\ F_{\text{y}|\mathbf{x}}(y_{\text{median}}|\boldsymbol{x})=0.5$$

  (כאשר $F_{\text{y}|\mathbf{x}}$ היא פונקציית הפילוג המצרפי של $\text{y}$ בהינתן $\mathbf{x}$).

• Misclassification rate: הערך הכי סביר (ה mode):

  $$h^*(\boldsymbol{x})=\underset{y}{\arg\max}\ p_{\text{y}|\mathbf{x}}(y|\boldsymbol{x})$$

דוגמא

בעבור הפילוג שמצאנו נחפש את החזאי אשר ממזער את ה misclassification rate.

במקרה הבנארי חזאי זה שווה ל:

את $p_{\text{y}|\mathbf{x}}(y|\boldsymbol{x})$ נוכל לחשב מתוך הפילוג המשותף באופן הבא:

דוגמא

אם כן, בכדי לבדוק האם עסקה מסויימת הינה הונאה או לא, עלינו לבדוק האם:

דוגמא

נציב את פונקציות הפילוג ששיערכנו קודם לכן ונקבל את החזאי הבא:

ה misclassification rate של חזאי זה על ה test set הינו 0.12.

ה bias וה variance של משערך

• המשערכים תלויים בצורה חזקה במדגם שאיתו אנו עובדים.
• נסתכל על האקראיות של השיערוך הנובעת מהאקראיות של המדגם.
• נשתמש בסימון $\mathbb{E}_{\mathcal{D}}$ בכדי לסמן תוחלת על פני הפילוג של המדגם.
• נגדיר bias ו variance של משערך

ה bias וה variance של משערך

Bias

בעבור שיערוך של גודל כל שהוא $z$ בעזרת משערך $\hat{z}_{\mathcal{D}}$, ה bias (היסט) של השיערוך מוגדר כ:

כאשר ההטיה שווה ל-0, אנו אומרים שהמשערך אינו מוטה (Unbiased).

Variance

ה variance (שונות) של המשערך יהיה:

מספר ה bins במונחים של bias ו variance

• ננסה לשערך את ה PDF של משתנה אקראי נורמאלי בעזרת היסטוגרמות בעלות 3, 7 ו 21 bins.

ה bias

נשרטט את ההיסטוגרמה הממוצעת לצד ה PDF האמיתי.

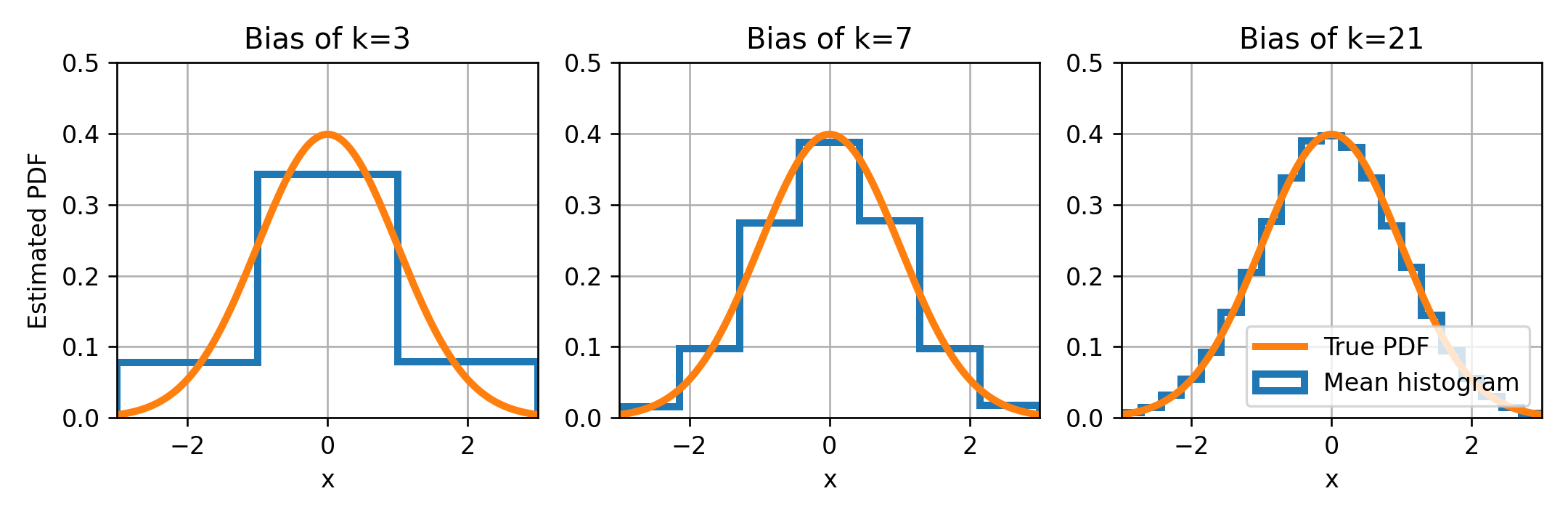
ה bias הוא ההפרש בין ההיסטוגרמה הממוצעת ל PDF האמיתי. ה bias קטן ככל שמספר ה bins גדל.

מספר ה bins במונחים של bias ו variance

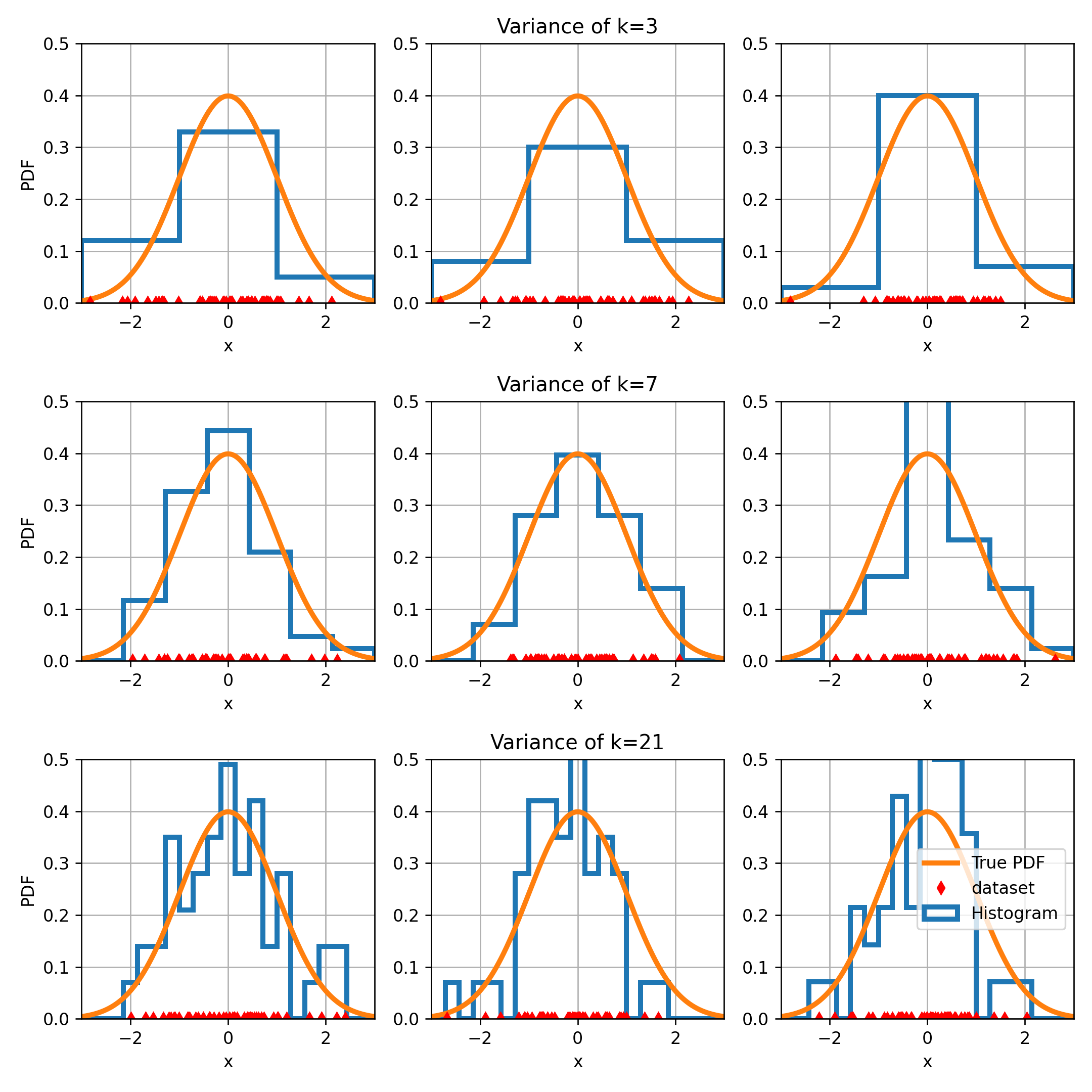
מספר ה bins במונחים של bias ו variance

ה variance

• בכל שורה בגרף הקודם מגרילים שלושה מדגמים ומחשבים להם את ההיסטוגרמה.
• אנו מצפים שבעבור מקרים שבהם ה variance נמוך השינויים יהיו קטנים ובעבור variance גבוה השינויים יהיו גדולים.
• ה variance גדל ככל שאנו מגדילים את כמות ה bins.

בדומה לחזאים בגישה הדיסקרימינטיבית, גם בהיסטוגרמה ישנו bias-variance tradeoff.