הרצאה 6 - SVM ושיטות גרעין

PDF

מה נלמד היום

סיווג לינארי

בפרק זה נעסוק בבעיית סיווג בינארי.
נסמן את שתי המחלקות ב $\text{y}=\pm1$ .
נעסוק במסווגים מהצורה:
$h(\boldsymbol{x})= \text{sign}(\boldsymbol{w}^{\top}\boldsymbol{x}+b) =\begin{cases} 1 & \boldsymbol{w}^{\top}\boldsymbol{x}+b>0\\ -1 & \text{else} \end{cases}$
חלוקה של המרחב לשני צידיו של על-מישור (hyperplane):
$\boldsymbol{w}^{\top}\boldsymbol{x}+b=0$
מישור זה מכונה מישור ההפרדה.

על-מישור (hyperplane)

הרחבה של מושג המישור למימדים שונים מ2.
במרחב ממימד $D$ , על-המישור יהיה ממימד $D-1$ .
בקורס זה נשתמש בשם מישור גם כדי להתייחס לעל-מישורים.
לא להתבלבל בין $\boldsymbol{w}^{\top}\boldsymbol{x}+b=0$ לבין $ax+b=y$ .

פרידות לינארית (linear separability)

במקרה שבו קיים מישור מפריד אשר מסווג את המדגם בצורה מושלמת (בלי טעויות סיווג) נאמר שהמדגם פריד לינארית.

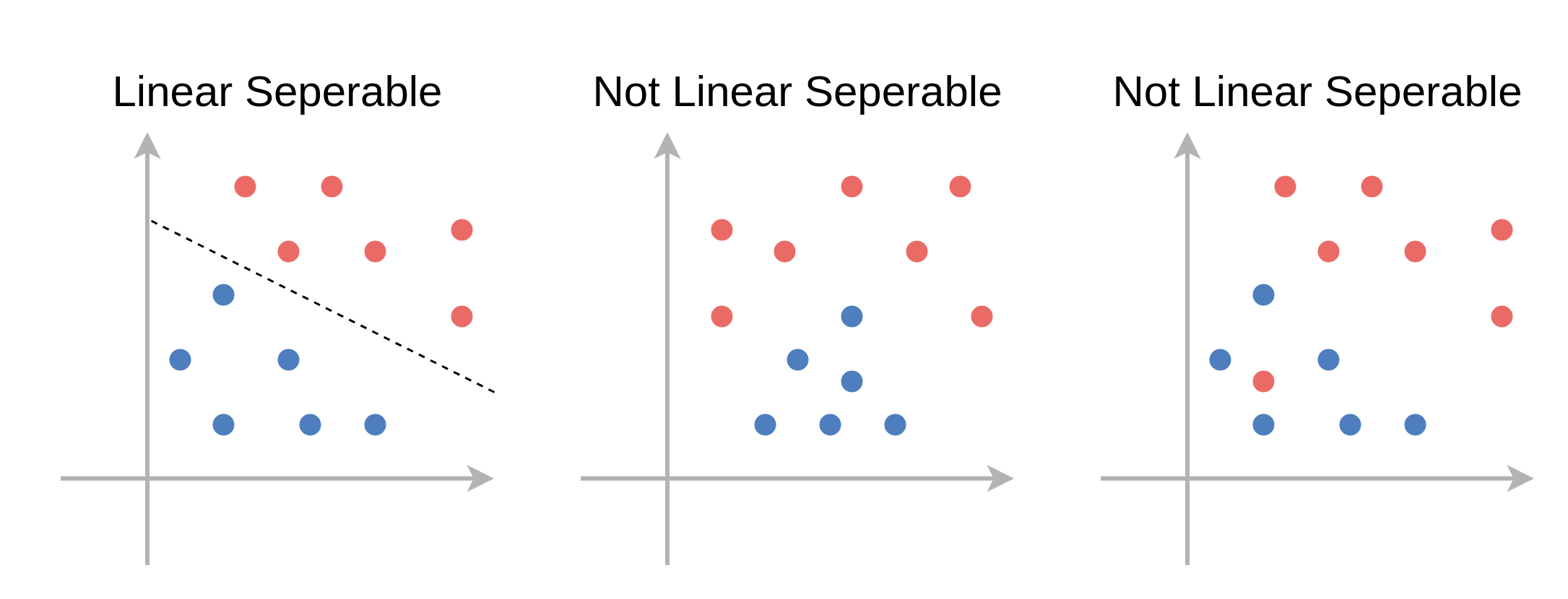
לרוב לא נוכל לדעת מראש האם מדגם הוא פריד לינארית או לא.

פרידות לינארית (linear separability)

למדגם פריד לינארית יהיה תמיד יותר ממשטח הפרדה אחד:

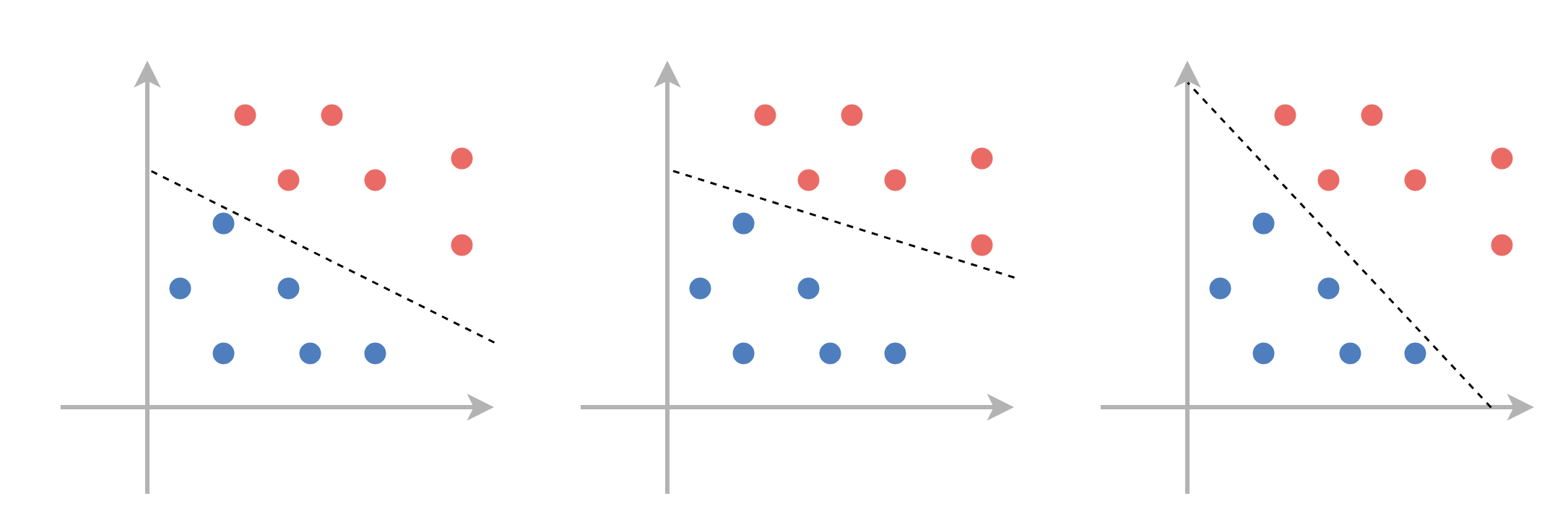
תזכורת - גאומטריה של המישור

נסתכל על הפונקציה $f(\boldsymbol{x})=\hat{\boldsymbol{w}}^{\top}\boldsymbol{x}$ . משוואה זו מטילה נקודות במרחב על המישור המוגדר על ידי $\hat{\boldsymbol{w}}$ (וקטור יחידה בכיוון של $\boldsymbol{w}$ ), ומודדת את האורך של הטלה זו.

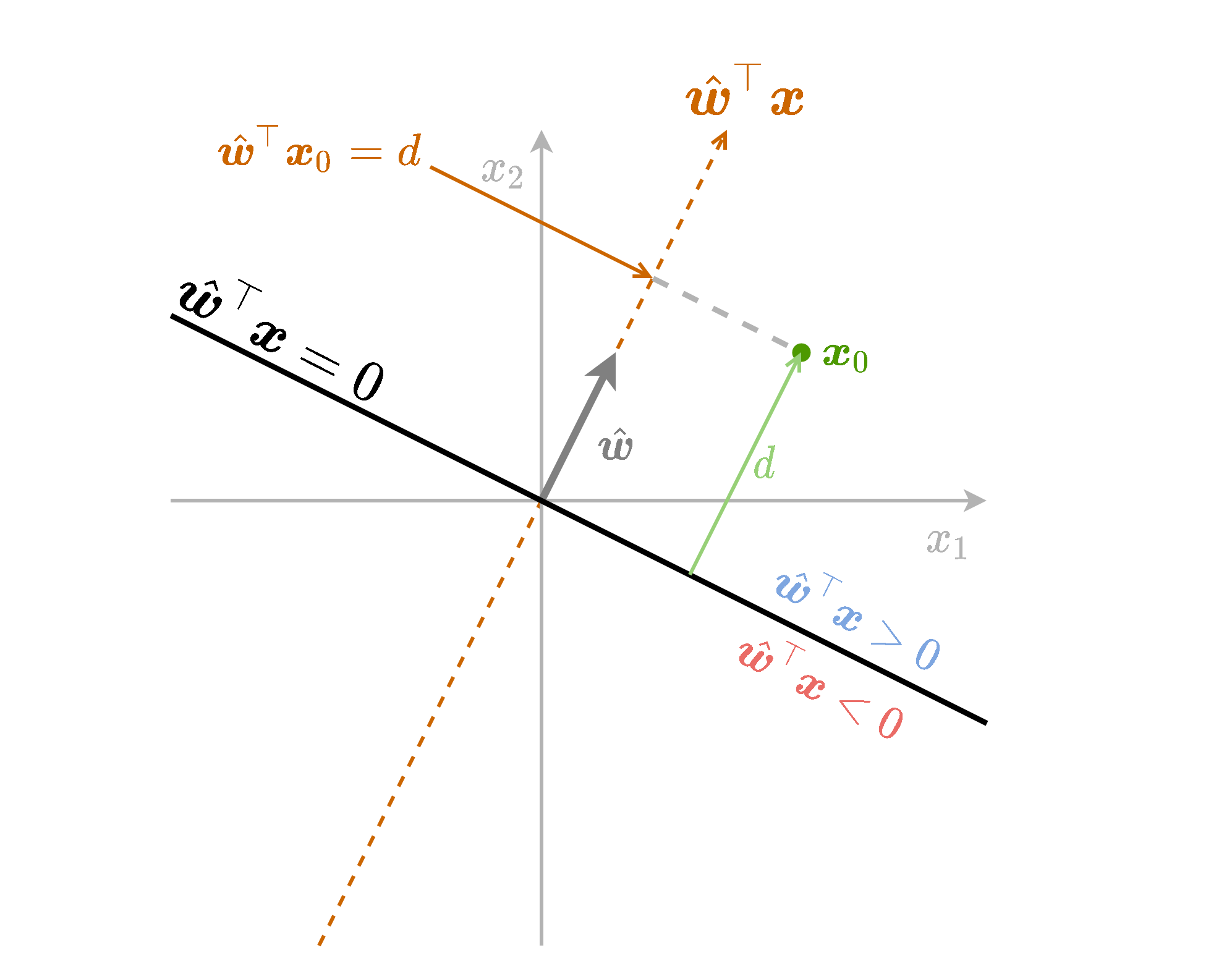
תזכורת - גאומטריה של המישור

מודדת את המרחק מהמישור $\hat{\boldsymbol{w}}^{\top}\boldsymbol{x}$ בתוספת של סימן אשר מציין את הצד של המישור.
נשתמש בשם signed distance (מרחק מסומן) כדי להתייחס לשילוב של המרחק מהמישור בתוספת הסימן.

תזכורת - גאומטריה של המישור

נחליף את הוקטור $\hat{\boldsymbol{w}}$ בוקטור $\boldsymbol{w}$ . נקבל פונקציה זהה המוכפלת ב $\lVert\boldsymbol{w}\rVert_2$ .

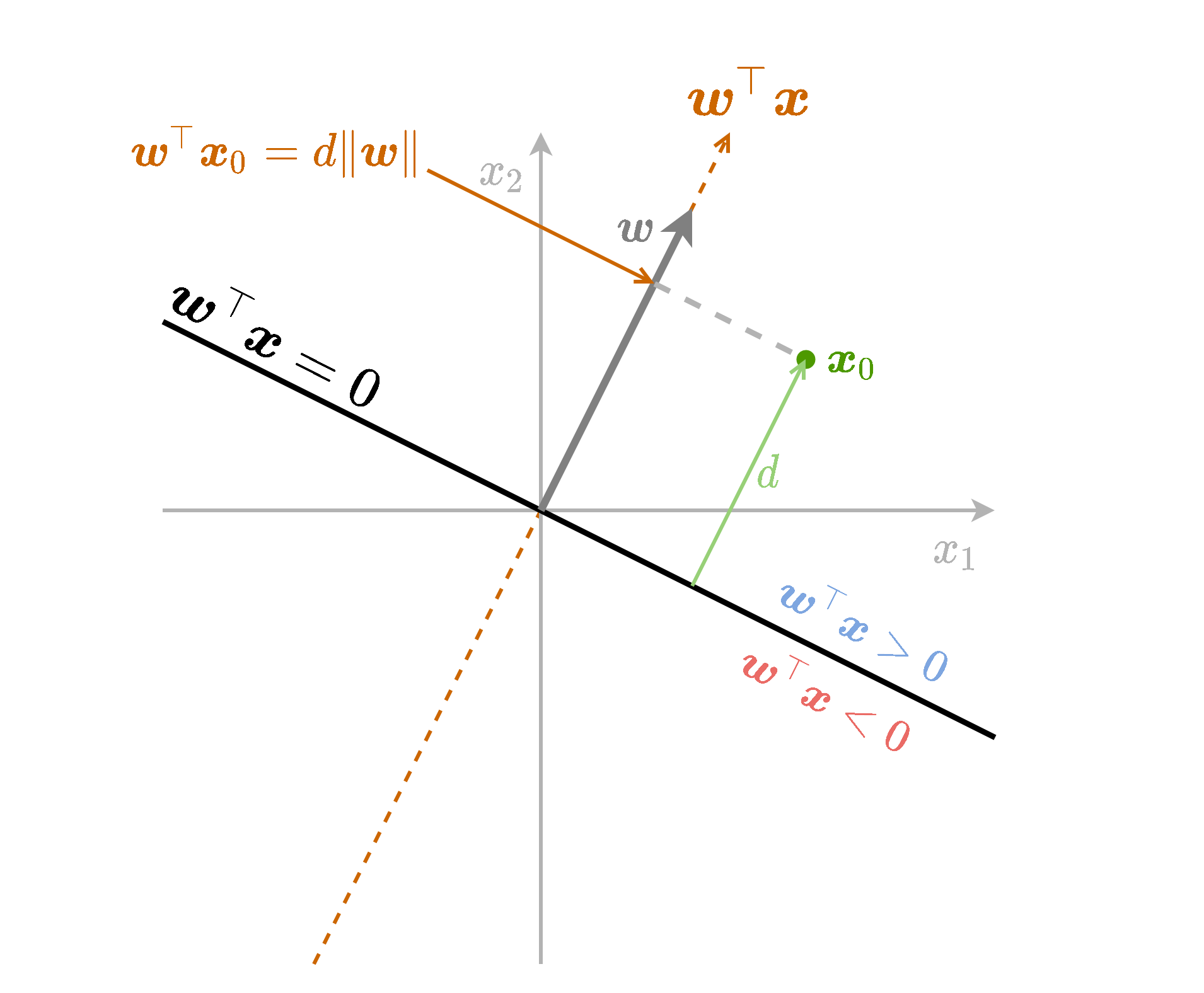
ה signed distance יהיה $d=\frac{1}{\lVert\boldsymbol{w}\rVert}\boldsymbol{w}^{\top}\boldsymbol{x}_0$ .

תזכורת - גאומטריה של המישור

נוסיף לפונקציה גם איבר היסט $b$ . ההוספה של הקבוע שקולה להזזה של נקודת ה-0.

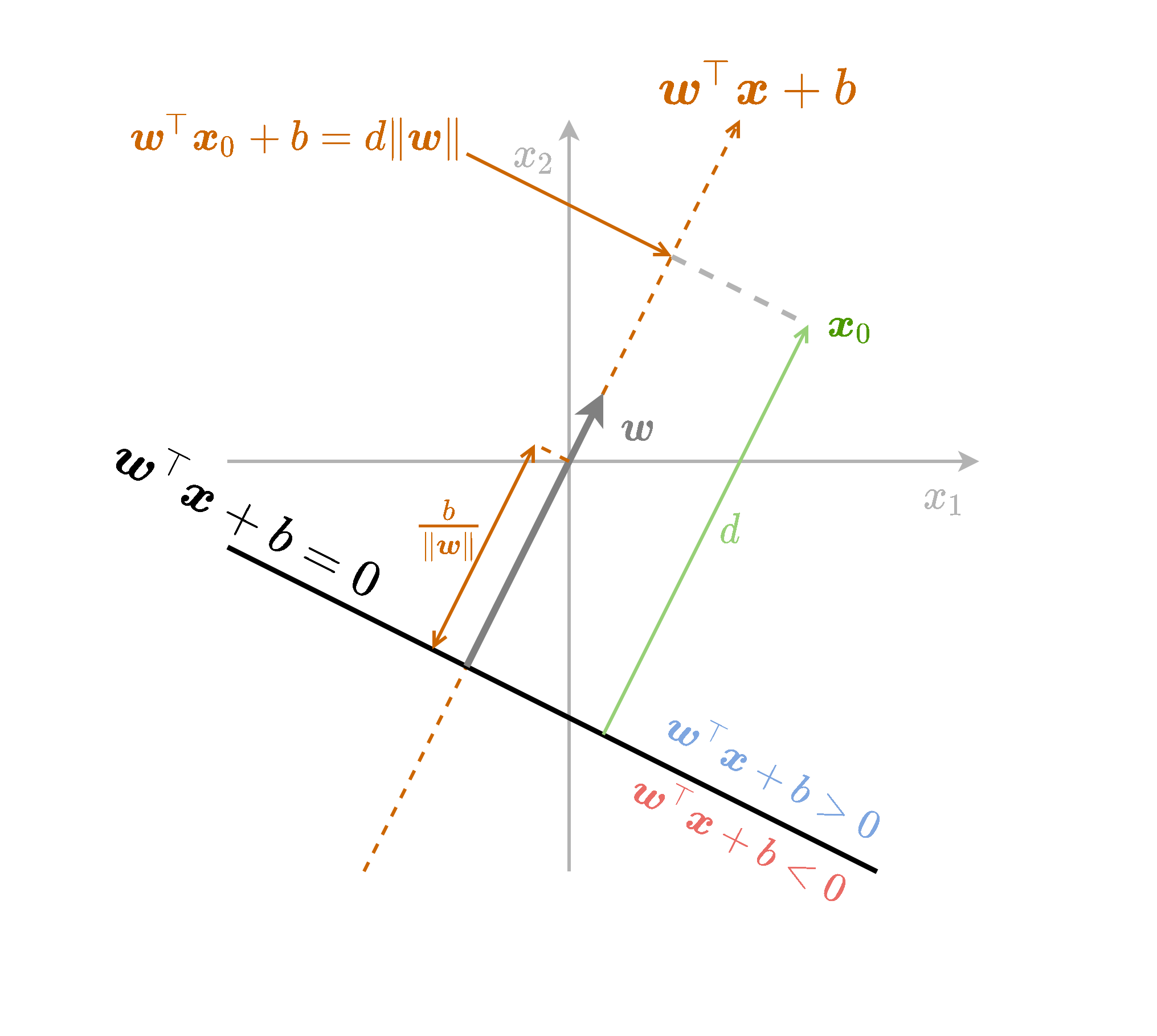
ה signed distance יהיה $d=\frac{1}{\lVert\boldsymbol{w}\rVert}(\boldsymbol{w}^{\top}\boldsymbol{x}_0+b)$

תזכורת - גאומטריה של המישור

נסכם את כל הנאמר לעיל בשרטוט הבא:

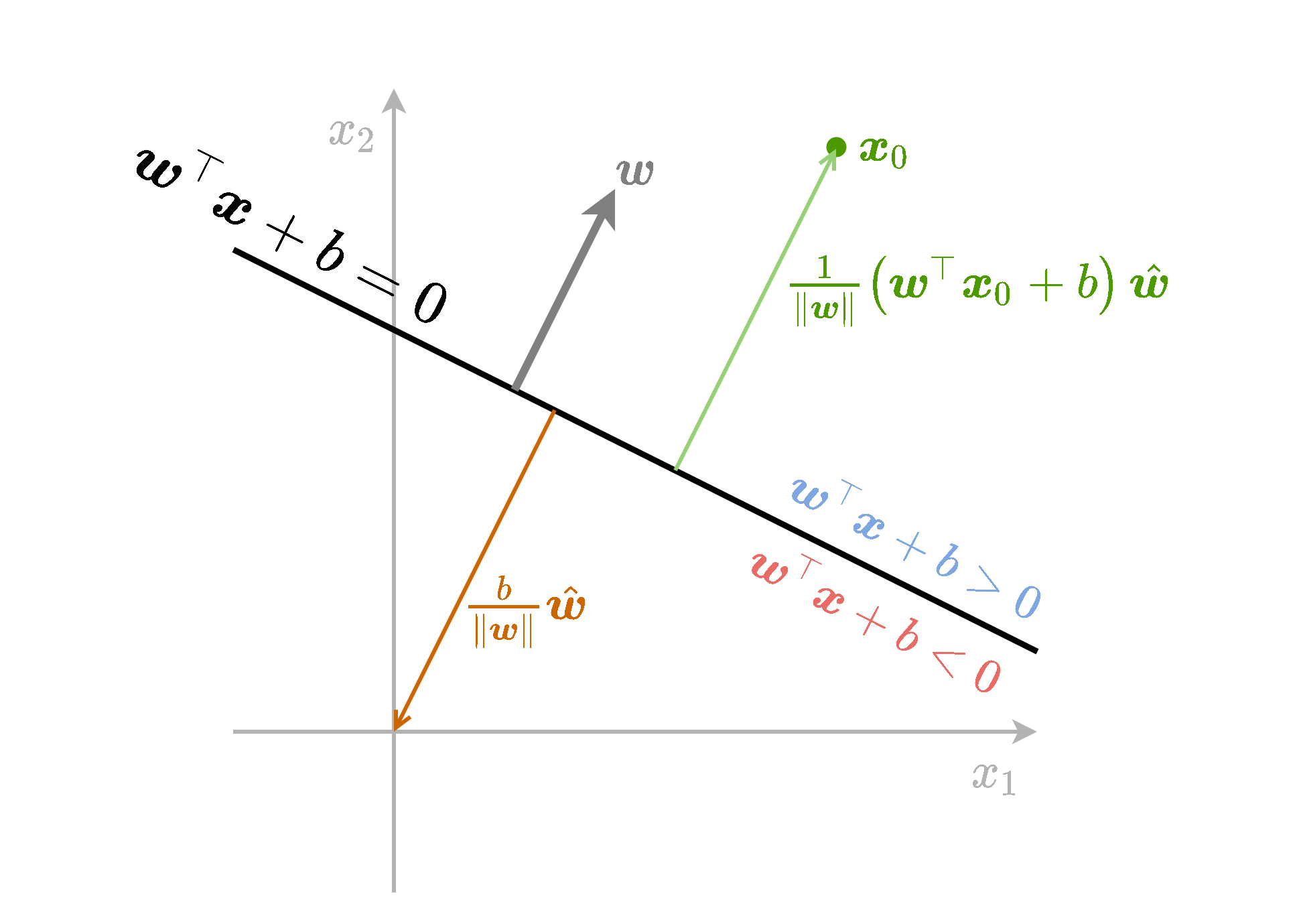
אינווריאנטיות לכפל בסקלר

אם נכפיל את גם את $\boldsymbol{w}$ וגם את $b$ בקבוע כל שהוא $\alpha$ שונה מאפס לא נשנה את מיקומו של המישור במרחב, זאת משום ש:

\begin{aligned} (\alpha\boldsymbol{w})^{\top}\boldsymbol{x}+(\alpha b)&=0\\ \Leftrightarrow\boldsymbol{w}^{\top}\boldsymbol{x}+b&=0 \end{aligned}

המשמעות הינה שיש מספר דרכים להגדיר את אותו מסווג לינארי.

Support Vector Machine (SVM)

אלגוריתם דיסקרימינטיבי לסיווג בינארי (מחפש מסווג טוב על המדגם).
Hard SVM מחפש מסווג לינארי למדגם שהוא פריד לינארית.
Soft SVM מרחיב את האלגוריתם למקרה שבו המדגם לא פריד לינארית.

Hard SVM

נרצה למצוא מישור הפרדה אשר יכליל בצורה טובה.
הנחה סבירה הינה שהפילוג של הנקודות יתרכז סביב הנקודות מהמדגם.

Hard SVM

Hard SVM מנסה למצוא מישור הפרדה אשר יהיה רחוק ככל האפשר מהנקודות שבמדגם.
או: נרצה שהמרחק מהמישור לנקודה הקרובה אליו ביותר יהיה מקסימאלי.

שאלה: למה זה רעיון טוב אינטואיטיבית?

Hard SVM

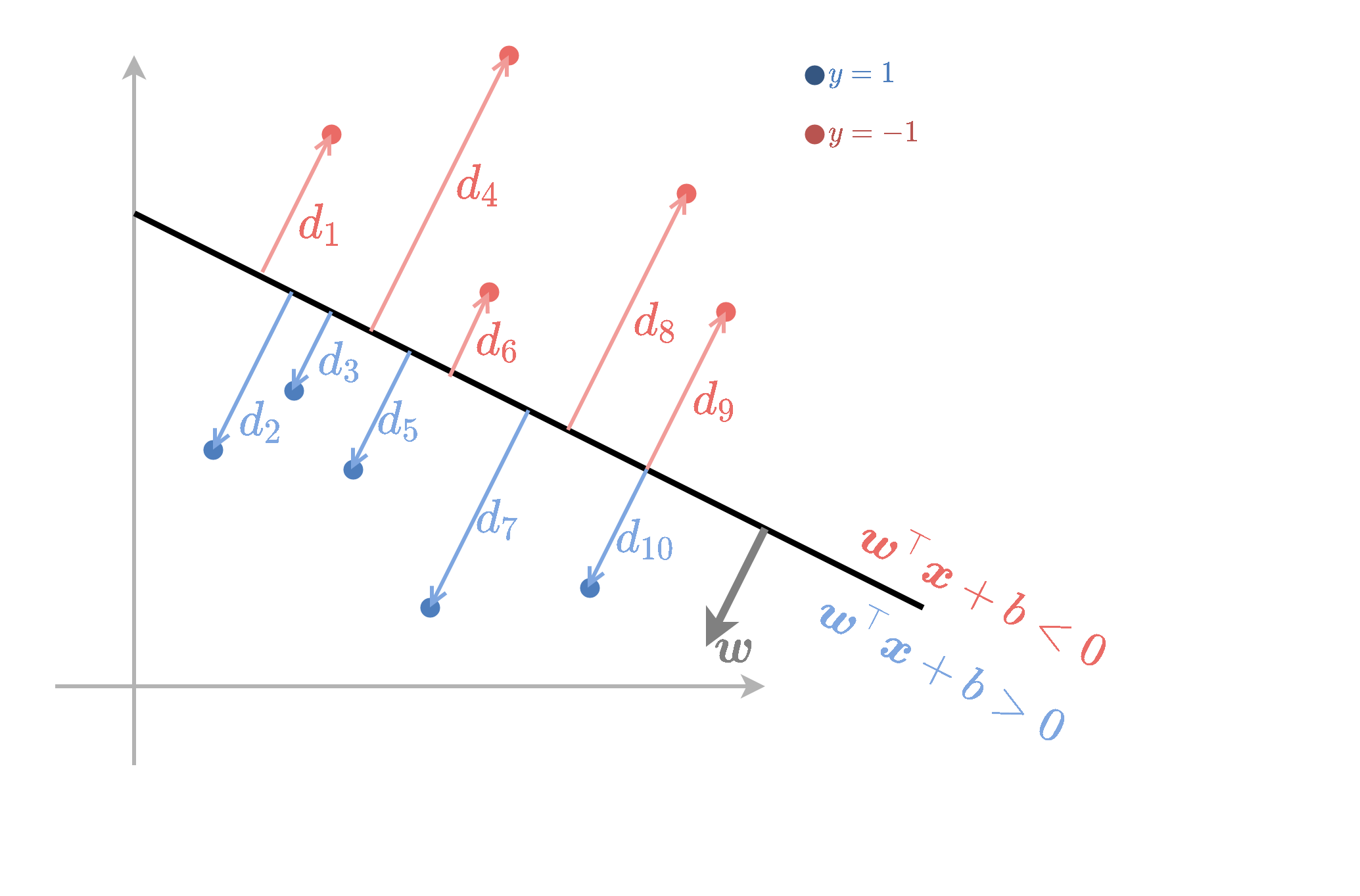
נסתכל על המכפלה בין המרחקים המסומנים של הנקודות לתוויות שלהם $\frac{1}{\lVert\boldsymbol{w}\rVert}(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)}+b)y^{(i)}$ .

כדי לקבל סיווג מושלם נרצה שכל המכפלות יהיו חיוביות.
בנוסף ננסה למקסם את המינימום של מכפלות אלו.

Hard SVM

בעיית האופטימיזציה שנרצה לפתור אם כן הינה:

\boldsymbol{w}^*,b^*=\underset{\boldsymbol{w},b}{\arg\max}\quad \underset{i}{\min}\left\{\frac{1}{\lVert\boldsymbol{w}\rVert}(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)}+b)y^{(i)}\right\}

ניתן לנסות לפתור באופן ישיר על ידי gradient descent.
בפועל העובדה שבבעיה מופיע $\min$ על כל המדגם מאד מקשה.
ניתן לפשט את הבעיה ולמצוא בעיה שקולה, שאותה נכנה הבעיה הפרימאלית.
את הבעיה הפרימאלית יהיה ניתן לפתור באופן יעיל בשיטות נומריות אחרות.

הפיתוח של הבעיה הפרימאלית

נוכל לבחור באופן שרירותי קבוע כפלי להכפיל בו את $\boldsymbol{w}$ ו- $b$ .
בפרט נוכל להוסיף דרישה ש:

\underset{i}{\min}\left\{(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)}+b)y^{(i)}\right\}=1

הפיתוח של הבעיה הפרימאלית

אם נוסיף את האילוץ הזה לבעיית האופטימיזציה נקבל:

\begin{aligned} \boldsymbol{w}^*,b^* =\underset{\boldsymbol{w},b}{\arg\max}\quad&\underset{i}{\min}\left\{\frac{1}{\lVert\boldsymbol{w}\rVert}(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)}+b)y^{(i)}\right\}\\ \text{s.t.}\quad&\underset{i}{\min}\left\{(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)}+b)y^{(i)}\right\}=1\\ =\underset{\boldsymbol{w},b}{\arg\max}\quad&\frac{1}{\lVert\boldsymbol{w}\rVert}\underset{i}{\min}\left\{(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)}+b)y^{(i)}\right\}\\ \text{s.t.}\quad&\underset{i}{\min}\left\{(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)}+b)y^{(i)}\right\}=1\\ =\underset{\boldsymbol{w},b}{\arg\max}\quad&\frac{1}{\lVert\boldsymbol{w}\rVert}\\ \text{s.t.}\quad&\underset{i}{\min}\left\{(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)}+b)y^{(i)}\right\}=1\\ =\underset{\boldsymbol{w},b}{\arg\min}\quad&\frac{1}{2}\lVert\boldsymbol{w}\rVert^2\\ \text{s.t.}\quad&\underset{i}{\min}\left\{(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)}+b)y^{(i)}\right\}=1\\ \end{aligned}

הפיתוח של הבעיה הפרימאלית

נוכל גם להחליף את האילוץ של $\underset{i}{\min}\left\{(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)}+b)y^{(i)}\right\}=1$ באילוץ:

(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)}+b)y^{(i)}\geq1\quad\forall i

מובטח שלפחות עבור אחת מהנקודות האילוץ יתקיים בשיוויון: אם זה לא המצב, תמיד נוכל לכפול את $\boldsymbol{w}$ ו- $b$ בקבוע חיובי קטן מספיק כך שהשיוויון יתקיים, וגם נשתפר בפתרון בעיית האופטימיזציה (שמנסה להקטין את $||\boldsymbol{w}||$ ).

הפיתוח של הבעיה הפרימאלית

קיבלנו את בעיית האופטימיזציה השקולה הבאה, היא הבעיה הפרימאלית:

\begin{aligned} \boldsymbol{w}^*,b^* =\underset{\boldsymbol{w},b}{\arg\min}\quad&\frac{1}{2}\lVert\boldsymbol{w}\rVert^2\\ \text{s.t.}\quad&(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)}+b)y^{(i)}\geq1\quad\forall i \end{aligned}

שימו לב למספר הגדול של האילוצים!

פרשנות

האילוץ דורש שהנקודות מהמדגם יהיו מחוץ לתחום:

1>\boldsymbol{w}^{\top}\boldsymbol{x}+b>-1

אשר נקרא השוליים (margin).

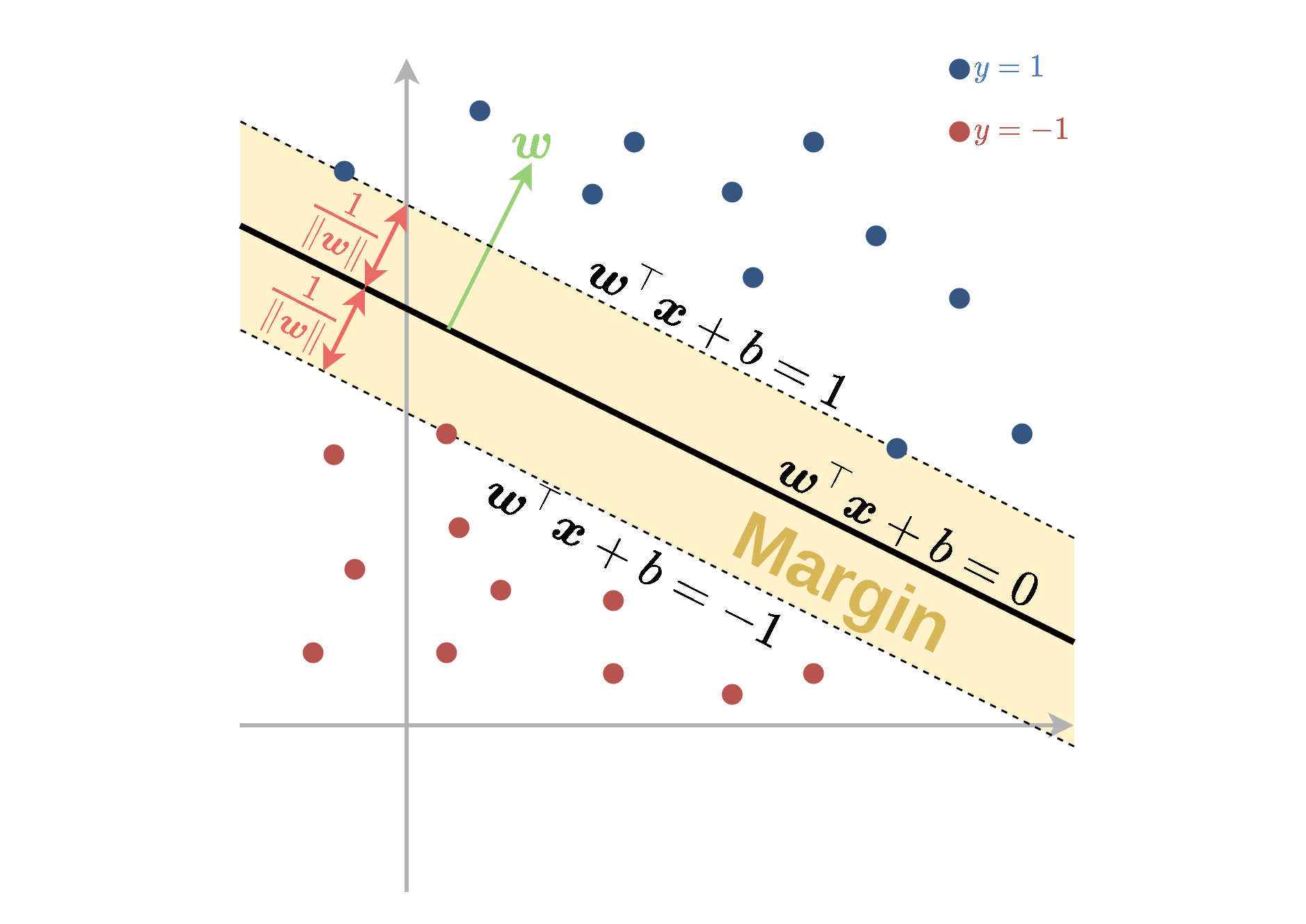
פרשנות

המרחק בין מישור ההפרדה לשפה של ה margin שווה ל $\frac{1}{\lVert\boldsymbol{w}\rVert}$ .
בעיית האופטימיזציה מנסה למזער את $\lVert\boldsymbol{w}\rVert$ ותתכנס למסווג בעל ה margin הגדול ביותר.

Support Vectors

ה support vectors הן הנקודות שיושבות על ה-margin והן מקיימות $y^{(i)}\left(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)}+b\right)=1$ .
רק נקודות אלו ישפיעו על הפתרון של בעיית האופטימיזציה.

הבעיה הדואלית

דרך שקולה נוספת לרישום של בעיית האופטימיזציה (ללא הוכחה):

נגדיר $N$ משתני עזר נוספים $\{\alpha_i\}_{i=1}^N$ בעזרתם ניתן לרשום את הבעיה הדואלית באופן הבא:

\begin{aligned} \left\lbrace\alpha_i\right\rbrace^* =\underset{\left\lbrace\alpha_i\right\rbrace}{\arg\max}\quad&\biggl[\sum_i\alpha_i-\frac{1}{2}\sum_{i,j}y^{(i)}y^{(j)}\alpha_i\alpha_j\boldsymbol{x}^{(i)\top}\boldsymbol{x}^{(j)}\biggr] \\ \text{s.t.}\quad &\alpha_i\geq0\quad\forall i\\ &\sum_i\alpha_iy^{(i)}=0 \end{aligned}

יש מספר גדול של משתנים, אך מעט אילוצים.

במודל ניתן למצוא נספח עם הסבר מפורט על אופטימיזציה קמורה בהקשר של SVM.

הבעיה הדואלית

\begin{aligned} \left\lbrace\alpha_i\right\rbrace^* =\underset{\left\lbrace\alpha_i\right\rbrace}{\arg\max}\quad&\biggl[\sum_i\alpha_i-\frac{1}{2}\sum_{i,j}y^{(i)}y^{(j)}\alpha_i\alpha_j\boldsymbol{x}^{(i)\top}\boldsymbol{x}^{(j)}\biggr] \\ \text{s.t.}\quad &\alpha_i\geq0\quad\forall i\\ &\sum_i\alpha_iy^{(i)}=0 \end{aligned}

שימו לב שהתלות במאפיינים רק דרך מכפלות פנימיות.

מתוך המשתנים $\{\alpha_i\}_{i=1}^N$ ניתן לשחזר את $\boldsymbol{w}$ אופן הבא:

\boldsymbol{w}=\sum_i\alpha_iy^{(i)}\boldsymbol{x}^{(i)}

רק נקודות המדגם שעבורן $\alpha$ חיובי תורמות לסכום.
הערה (הרחבה למתעניינים): המשתנים $\alpha$ הם כופלי לגרנז' מהבעיה הפרימאלית.

הקשר בין $\alpha_i$ ו support vectors.

.	.	.
נקודות רחוקות מה margin	$y^{(i)}\left(\boldsymbol{w}^{\top}x^{(i)}+b\right)>1$	$\alpha_i=0$
נקודות על ה margin (שהם support vectors)	$y^{(i)}\left(\boldsymbol{w}^{\top}x^{(i)}+b\right)=1$	$\alpha_i\geq0$

חישוב $b$

נבחר נקודה מסויימת שעבורה $\alpha_i>0$ .
נקודה כזו בהכרח תהיה support vector ותקיים $y^{(i)}\left(\boldsymbol{w}^{\top}x^{(i)}+b\right)=1$ .
מתוך משוואה זו ניתן לחלץ את $b$ .

Soft SVM

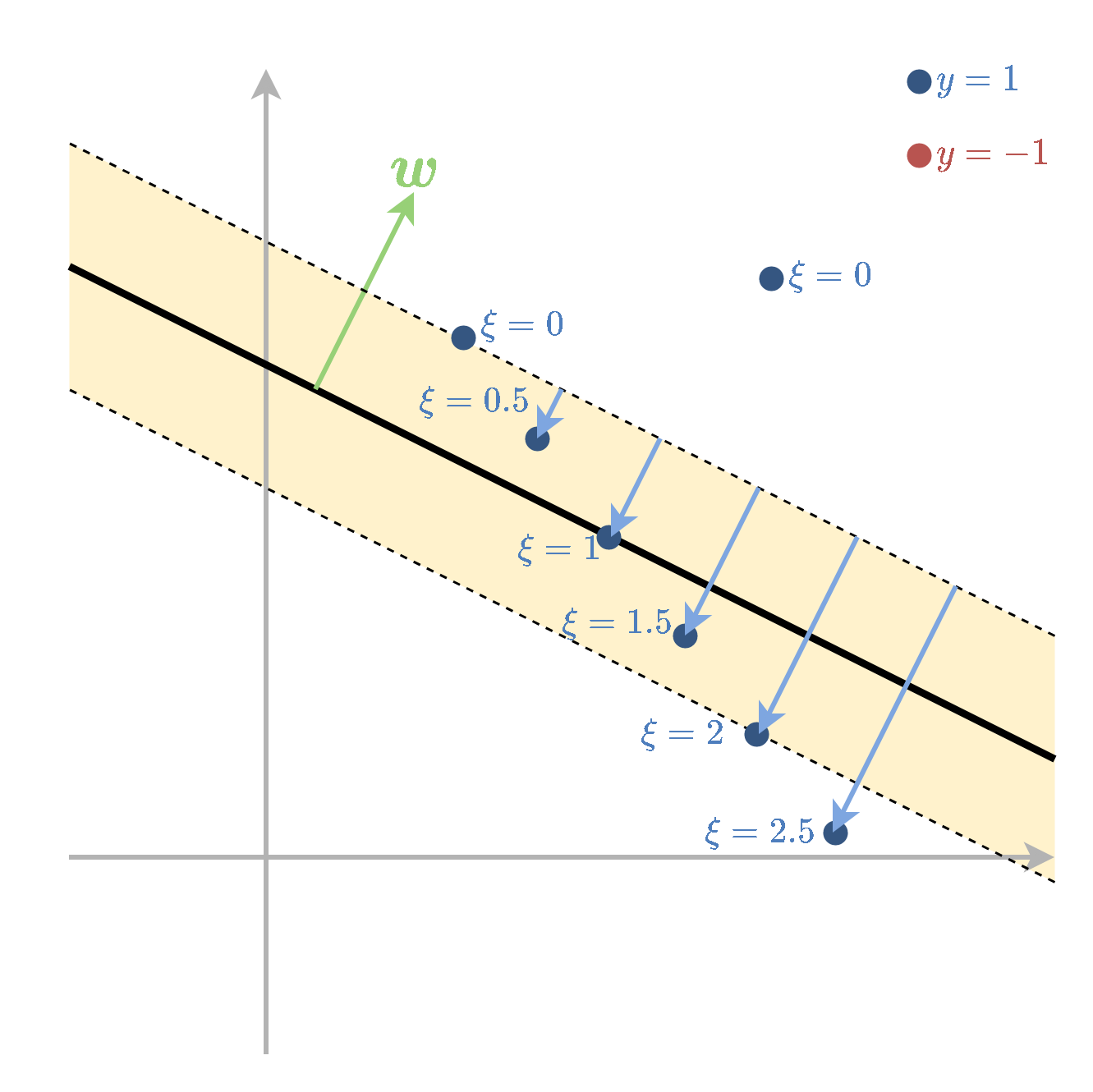
מתייחס למקרה שבו המדגם אינו פריד לינארית.
מאפשרים לנקודות המדגם להיכנס לתוך השוליים ואף לחצות אותם.
על כל חריגה כזו משלמים קנס בפונקציית המטרה.

Soft SVM

את החריגה של הדגימה ה $i$ נסמן ב $\frac{1}{\lVert\boldsymbol{w}\rVert}\xi_i$ .
המשתנים $\xi_i$ נקראים slack variables.

Soft SVM

ובעיית האופטימיזציה הפרימאלית תהיה

\begin{aligned} \boldsymbol{w}^*,b^*,\{\xi_i\}^*= \underset{\boldsymbol{w},b,\{\xi_i\}}{\arg\min}\quad&\biggl[\frac{1}{2}\left\lVert\boldsymbol{w}\right\rVert^2+C\sum_{i=1}^N\xi_i\biggr] \\ \text{s.t.}\quad &y^{(i)}\left(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)}+b\right)\geq1-\xi_i\quad\forall i\\ &\xi_i\geq0\quad\forall i \end{aligned}

כאשר $C$ הוא היפר-פרמטר אשר קובע את גודל הקנס בפונקציית המחיר על כל חריגה. בבעיה הפרימאלית לא היה היפר-פרמטר.

שאלה: מה ההשפעה של ערכים שונים של המשתנים $\xi_i$ ?

Soft SVM

הבעיה הדואלית הינה

\begin{aligned} \left\lbrace\alpha_i\right\rbrace^* =\underset{\left\lbrace\alpha_i\right\rbrace}{\arg\max}\quad&\biggl[\sum_i\alpha_i-\frac{1}{2}\sum_{i,j}y^{(i)}y^{(j)}\alpha_i\alpha_j\boldsymbol{x}^{(i)\top}\boldsymbol{x}^{(j)}\biggr] \\ \text{s.t.}\quad &0\leq\alpha_i\leq C\quad\forall i\\ &\sum_i\alpha_iy^{(i)}=0 \end{aligned}

Soft SVM

עבור ה support vectors מתקיים: $y^{(i)}\left(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)}+b\right)=1-\xi_i$

תכונות:

.	.	.
נקודות שמסווגות נכון ורחוקות מה margin	$y^{(i)}\left(\boldsymbol{w}^{\top}x^{(i)}+b\right)>1$	$\alpha_i=0$
נקודות על ה margin (שהם support vectors)	$y^{(i)}\left(\boldsymbol{w}^{\top}x^{(i)}+b\right)=1$	$0\leq\alpha_i\leq C$
נקודות שחורגות מה margin (גם support vectors)	$y^{(i)}\left(\boldsymbol{w}^{\top}x^{(i)}+b\right)=1-\xi_i$	$\alpha_i=C$

כאשר המקרה האחרון כולל נקודות המסווגות נכון ולא נכון.

מאפיינים: תזכורת

סיווג לינארי מוגבל, ולכן נרצה להרחיב לסיווג לא לינארי.

נוכל תמיד להחליף את וקטור המשתנים $\boldsymbol{x}$ בוקטור חדש:
$\boldsymbol{x}_{\text{new}}=\Phi(\boldsymbol{x})$
$\Phi$ היא פונקציה אשר נבחרה מראש ונקראת פונקציית המאפיינים.
אם הממד של $\Phi$ מספיק גבוה, ניתן תמיד להגיע להפרדה לינארית במרחב הרב-ממדי (דורש הוכחה).

מאפיינים: דוגמה

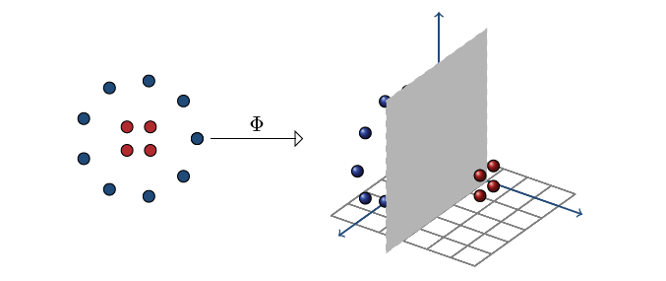
נשים לב שהמסווג האופטימלי הוא ריבועי במרחב המקורי.

נשתמש בפונקציית המאפיינים

\Phi(x) = (x_1,x_2,x_1x_2,x_1^2,x_2^2,1)

ונקבל $w^\top\Phi(x)$ שהוא לינארי ב- $w$ .

האיור מתוך, Mohri et-al, Foundation of Machine Learning

פונקציות גרעין

במקרים רבים החישוב של $\Phi(\boldsymbol{x})$ יכול להיות מסובך אך קיימת דרך לחשב בצורה יעילה את הפונקציה $K(\boldsymbol{x}_1,\boldsymbol{x}_2)=\Phi(\boldsymbol{x}_1)^{\top}\Phi(\boldsymbol{x}_2)$ .
הפונקציה $K$ נקראת פונקציית גרעין.
יתרה מזאת, ייתכנו מצבים שבהם וקטור המאפיינים הוא אינסופי אך פונקציית הגרעין היא פשוטה לחישוב.

נציג שתי פונקציות גרעין נפוצות:

גרעין גאוסי: $K(\boldsymbol{x}_1,\boldsymbol{x}_2)=\exp\left(-\frac{\lVert\boldsymbol{x}_1-\boldsymbol{x}_2\rVert_2^2}{2\sigma^2}\right)$ כאשר $\sigma$ פרמטר שיש לקבוע.
גרעין פולינומיאלי: $K(\boldsymbol{x}_1,\boldsymbol{x}_2)=(1+\boldsymbol{x}_1^{\top}\boldsymbol{x}_2)^p$ כאשר $p\geq1$ פרמטר שיש לקבוע.

Kernel Trick in SVM

הרעיון ב kernel trick הינו לעשות שימוש בפונקציית הגרעין על מנת להשתמש ב SVM עם מאפיינים מבלי לחשב את $\Phi$ באופן ישיר.

עבור פונקציית מאפיינים $\Phi$ עם פונקציית גרעין $K$ הבעיה הדואלית של SVM הינה:

\begin{aligned} \left\lbrace\alpha_i\right\rbrace^* =\underset{\left\lbrace\alpha_i\right\rbrace}{\arg\max}\quad&\sum_i\alpha_i-\frac{1}{2}\sum_{i,j}y^{(i)}y^{(j)}\alpha_i\alpha_j\textcolor{blue}{K(\boldsymbol{x}^{(i)},\boldsymbol{x}^{(j)})} \\ \text{s.t.}\quad &\alpha_i\geq0\quad\forall i\\ &\sum_i\alpha_iy^{(i)}=0 \end{aligned}

Kernel Trick in SVM

\begin{aligned} \left\lbrace\alpha_i\right\rbrace^* =\underset{\left\lbrace\alpha_i\right\rbrace}{\arg\max}\quad&\sum_i\alpha_i-\frac{1}{2}\sum_{i,j}y^{(i)}y^{(j)}\alpha_i\alpha_j\textcolor{blue}{K(\boldsymbol{x}^{(i)},\boldsymbol{x}^{(j)})} \\ \text{s.t.}\quad &\alpha_i\geq0\quad\forall i\\ &\sum_i\alpha_iy^{(i)}=0 \end{aligned}

שאלה: מה הקשר לבעיה הדואלית בשקף 25?

בעיית אופטימיזציה זו מגדירה את המשתנים $\{\alpha_i\}$ בלי צורך לחשב את $\Phi$ באופן מפורש בשום שלב.

Kernel Trick in SVM

באופן כללי, הפרמטר $\boldsymbol{w}$ נתון על ידי:

\boldsymbol{w}=\sum_i\alpha_iy^{(i)}\Phi(\boldsymbol{x}^{(i)})

אשר מצריך חישוב של $\Phi$ . ניתן להימנע מכך על ידי הצבה של $\boldsymbol{w}$ כמו שהוא ישירות לחזאי.

\begin{aligned} h(\boldsymbol{x}) &=\text{sign}(\boldsymbol{w}^{\top}\Phi(\boldsymbol{x})+b)\\ &=\text{sign}(\sum_i\alpha_iy^{(i)}\Phi(\boldsymbol{x}^{(i)})^{\top}\Phi(\boldsymbol{x})+b)\\ &=\text{sign}(\sum_i\alpha_iy^{(i)}K(\boldsymbol{x}^{(i)},\boldsymbol{x})+b)\\ \end{aligned}

בדרך זו אנו יכולים לאמן להשתמש בחזאי אשר אומן בעבור וקטור מאפיינים $\Phi$ מבלי לחשב בשום שלב את $\Phi$ באופן מפורש.

סיכום: תכונות מסווג SVM

במקרה הפריד לינארית:

איטואיטיבי וקל להבנה - ייצוג פשוט של הפתרון
מבטיח ביצועי הכללה טובים בזכות השוליים הרחבים (לא הראינו) - סוג של רגולריזציה
יעיל חישובית

במקרה הלא פריד לינארית:

מתווסף היפר-פרמטר שיש לכוון
הבנה אינטואיטיבית פחותה
מעבר פשוט ונוח למסווגים לא לינאריים ע"י שיטות גרעין

הרצאה 6 - SVM ושיטות גרעין

מה נלמד היום

סיווג לינארי

על-מישור (hyperplane)

פרידות לינארית (linear separability)

פרידות לינארית (linear separability)

תזכורת - גאומטריה של המישור

תזכורת - גאומטריה של המישור

תזכורת - גאומטריה של המישור

תזכורת - גאומטריה של המישור

תזכורת - גאומטריה של המישור

אינווריאנטיות לכפל בסקלר

Support Vector Machine (SVM)

Hard SVM

Hard SVM

Hard SVM

Hard SVM

הפיתוח של הבעיה הפרימאלית

הפיתוח של הבעיה הפרימאלית

הפיתוח של הבעיה הפרימאלית

הפיתוח של הבעיה הפרימאלית

פרשנות

פרשנות

Support Vectors

הבעיה הדואלית

הבעיה הדואלית

הקשר בין αi\alpha_iαi​ ו support vectors.

חישוב bbb

Soft SVM

Soft SVM

Soft SVM

Soft SVM

Soft SVM

מאפיינים: תזכורת

מאפיינים: דוגמה

פונקציות גרעין

Kernel Trick in SVM

Kernel Trick in SVM

Kernel Trick in SVM

סיכום: תכונות מסווג SVM

הקשר בין $\alpha_i$ ו support vectors.

חישוב $b$