הרצאה 5 - Bagging and Boosting

PDF

מה נלמד היום

Ensemble Methods

בהרצאה הזו נציג שתי שיטות אשר בעזרתן ניתן לשפר את הביצועים של אלגוריתמים קיימים על ידי שימוש בסט של חזאים. סט זה מכונה לרוב ensemble (מכלול).

תזכורת הטיה ושונות

  • מתייחסים לפילוג של שגיאת החיזוי על פני מדגמים שונים.
  • נתייחס למדגם כאל משתנה אקראי.

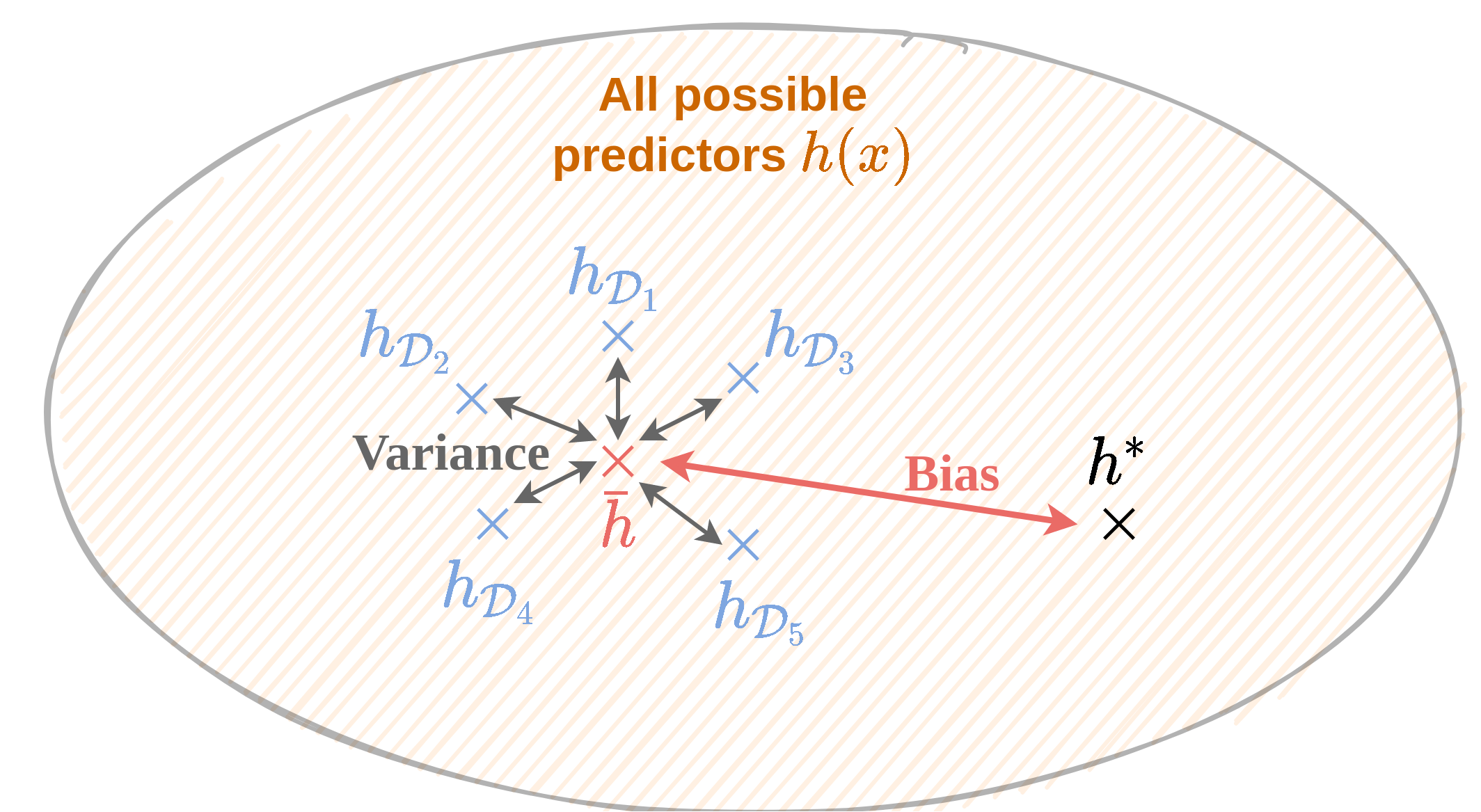
תזכורת הטיה ושונות

  • החיזוי הממוצע: hˉ(x)=ED[h(x)]\bar{h}(\boldsymbol{x})=\mathbb{E}_{\mathcal{D}}\left[h(\boldsymbol{x})\right]
  • החיזוי האופטימלי h∗(x)h^*(\boldsymbol{x}).
  • ההטיה היא ההפרש בין החיזוי הממוצע לחיזוי האופטימלי.
  • השונות היא ED[(hD(x)−hˉ(x))2]\mathbb{E}_{\mathcal{D}}\left[(h_{\mathcal{D}}(\boldsymbol{x})-\bar{h}(\boldsymbol{x}))^2\right]

תזכורת הטיה ושונות

  • מודלים בעלי יכולת ייצוג נמוכה יסבלו לרוב מהתאמת חסר אשר יתבטא בהטיה גבוהה ושונות נמוכה
  • מודלים בעלי יכולת ייצוג גבוהה יסבלו לרוב מהתאמת יתר אשר יתבטא בשונות מאד גבוהה והטיה נמוכה

Bagging ו Boosting

כעת נוכל להסביר מה bagging ו boosting מנסים לעשות:

  • ב bagging ננסה לקחת מכלול של חזאים עם שונות גבוהה ולשלב ביניהם כדי ליצור חזאי עם שונות נמוכה יותר.
  • ב boosting ננסה לקחת מכלול של חזאים עם הטיה גבוהה ולשלב ביניהם כדי ליצור חזאי עם הטיה נמוכה יותר.

שאלה: דוגמאות לכל אחד מהמקרים

Bagging

נהיה מעוניינים לייצר מכלול (ensemble) של חזאים בעלי הטיה נמוכה אך שונות גבוהה ואז לשלב ביניהם על מנת להקטין את השונות.


אחת הבחירות הנפוצות לחזאים שכאלה ב bagging היא עצי החלטה עמוקים (ללא pruning).


השם Bagging הוא הלחם של המילים bootstrapping ו aggregation, שהם שני שלבי השיטה.

גישה נאיבית

  • לו יכלנו לייצר כמה מדגמים בלתי תלויים, היינו יכולים לבנות חזאי עבור כל מדגם ולמצע על החזאים על מנת להקטין את השונות של השגיאת החיזוי.
  • בפועל לרוב יהיה בידינו רק מדגם יחיד שאיתו נצטרך לעבוד.
  • ניתן לייצר מספר מדגמים על ידי חלוקת המדגם הקיים, אך לרוב העובדה שהמדגמים הם משמעותית קטנים מהמדגם המקורי תגדיל את השונות.

Bootstrapping

אופציה חלופית אשר שומרת על גודל המדגם, אך מתפשרת על דרישת חוסר התלות בין המדגמים ובין הדגימות.


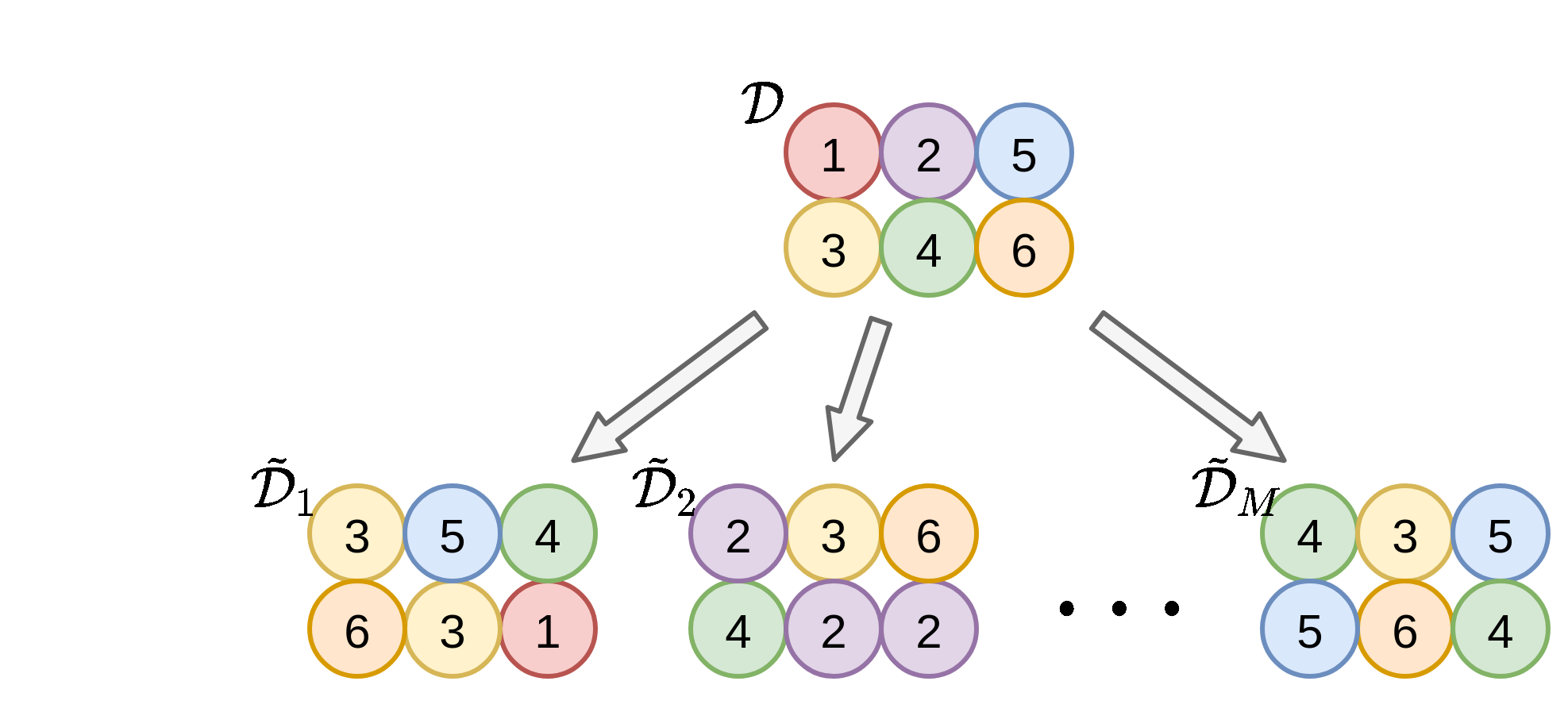
Bootstrapping

בשיטה זו אנו נייצר מדגמים חדשים על ידי דגימה מחדש של המדגם הנתון. הדגימה הינה עם חזרות.

שאלה: מהי דגימה עם חזרות ודגימה ללא חזרות? מה ניתן לומר על התלות בין הדגימות המתקבלות?

Bootstrapping

  • הסיכוי של דגימה כלשהיא להופיע ב D~\tilde{\mathcal{D}} הינה 1−(1−1N)N~1-(1-\frac{1}{N})^{\tilde{N}}.
  • כאשר N~=N\tilde{N}=N ו N→∞N\rightarrow\infty, סיכוי זה הולך ל 1−e−1≈63%1-e^{-1}\approx63\%.

Aggregation: שילוב חזאים לחזאי יחיד

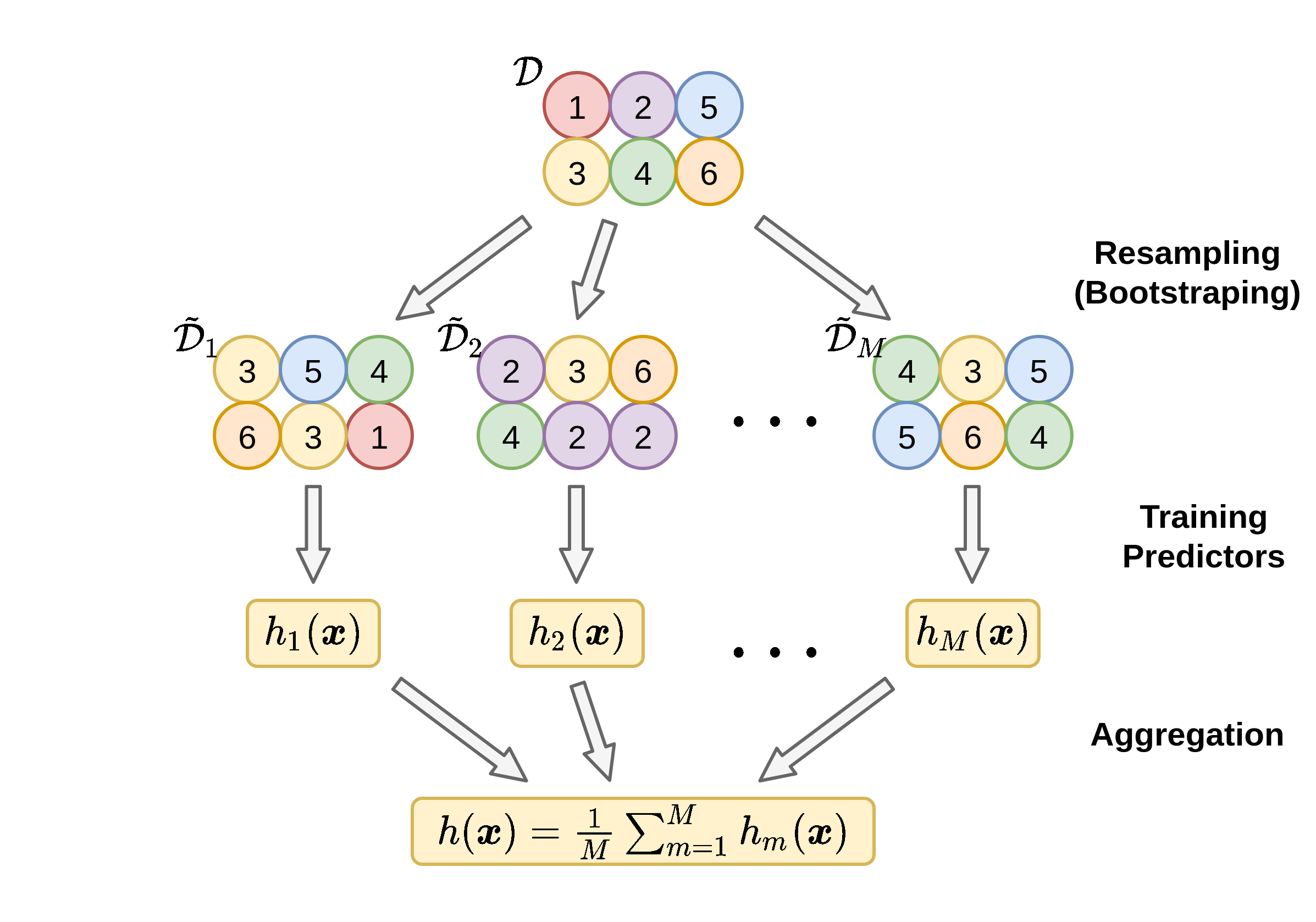
  • נייצר MM מדגמים חדשים בגודל זהה למדגם המקורי N~=N\tilde{N}=N.
  • עבור כל אחד מהמדגמים D~m\tilde{\mathcal{D}}_m נבנה חזאי h~m\tilde{h}_m.
  • נקבץ את כל החזאים על מנת לקבל את החזאי הכולל.

Aggregation: שילוב חזאים לחזאי יחיד

  • עבור בעיות רגרסיה: נמצע את תוצאת החיזוי של כל החזאים:
h(x)=1M∑m=1Mh~m(x)h(\boldsymbol{x})=\frac{1}{M}\sum_{m=1}^M \tilde{h}_m(\boldsymbol{x})
  • עבור בעיות סיווג: נבצע majority voting:
h(x)=majority({h~1(x),h~2(x),…,h~M(x)})h(\boldsymbol{x})=\text{majority}(\{\tilde{h}_1(\boldsymbol{x}),\tilde{h}_2(\boldsymbol{x}),\dots,\tilde{h}_M(\boldsymbol{x})\})

Aggregation: שילוב חזאים לחזאי יחיד

  • מספר המדגמים MM נע בין עשרות מדגמים לאלפים.
  • לרוב נשתמש באותה השיטה על מנת לבנות את כל החזאים.
  • כל מסווג יכול להיות עץ החלטה מלא!

Out Of Bag Error Estimation (לקריאה עצמית - לא למבחן)

  • ניתן להעריך את ביצועי המודל ללא צורך ב test / validation set.
  • הרעיון הינו להשתמש בעובדה שכל אחד מהמדגמים מכיל רק חלק מהדגימות.

Random Forest (לקריאה עצמית - לא למבחן)

  • שילוב של עצי החלטה עם bagging + תוספת.
  • תוספת - בחירה אקראית של תת-קבוצות של רכיבים בפיצולים בצומת - מקטין את הקורלציה בין העצים השונים.

  • שיטה מאד יעילה ונפוצה.

Random Forest (לקריאה עצמית - לא למבחן)

מדוע השיטה עובדת?

  • הפחתה בהתאמת יתר
  • דיוק גבוה
  • חסינות בפני נתונים בעייתים (כגון נתונים חסרים, ouliers)
  • קיימות הבטחות תאורטיות (לא נדון)
  • מה החסרון לעומת עצי החלטה?

Boosting

  • ננסה להשתמש במכלול של חזאים בעלי הטיה גבוהה אך שונות נמוכה כדי ליצור חזאי כולל בעל שונות נמוכה.
  • נתמקד בבעיות סיווג בינארי.
  • התוויות בבעיה הן (מטעמי סימטריה) y=±1\text{y}=\pm1.

בעיית ה boosting המקורית
(לקריאה עצמאית - לא למבחן)

  • מהו לומד חזק?
  • מהו לומד חלש?
  • האם כל לומד הוא בעצם גם לומד חזק?

הרחבה ברשימות

AdaBoost (adaptive-boosting)

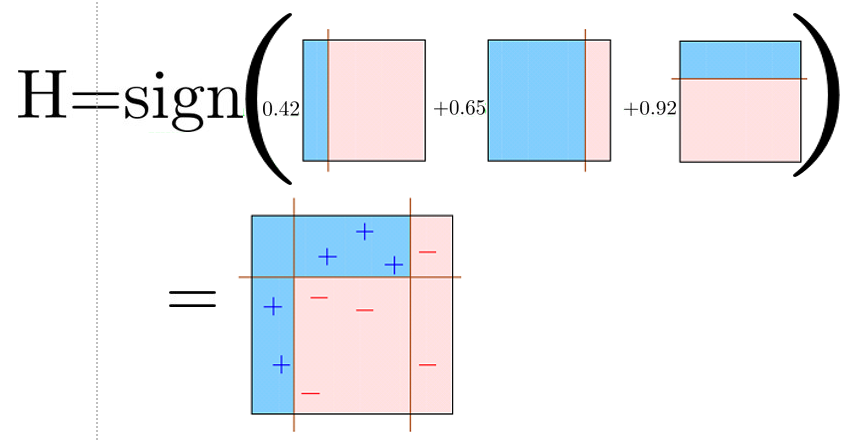
בהינתן אוסף של חזאים "חלשים" h~(x)\tilde{h}(\boldsymbol{x}) בעלי הטיה גבוהה, שיטה זו מנסה לבנות חזאי מהצורה

h(x)=sign(∑m=1Mαmh~m(x))h(\boldsymbol{x})=\text{sign}\left(\sum_{m=1}^M\alpha_m \tilde{h}_m(\boldsymbol{x})\right)

כך ש h(x)h(\boldsymbol{x}) יהיה בעל הטיה נמוכה.

  • בחירה פופולרית של מסווגים כאלה הינה עצי החלטה בעומק 1 המכונים stumps (עצים עם פיצול יחיד).

החסם על ה misclassification rate

נראה שעבור חזאי מהצורה של

h(x)=sign(∑m=1Mαmh~m(x))h(\boldsymbol{x})=\text{sign}\left(\sum_{m=1}^M\alpha_m \tilde{h}_m(\boldsymbol{x})\right)

שגיאת 0-1 האמפירית חסומה מלמעלה על ידי:

1N∑i=1Nexp⁡(−∑m=1Mαmy(i)h~m(x(i)))\frac{1}{N}\sum_{i=1}^N\exp\left(-\sum_{m=1}^M\alpha_m y^{(i)}\tilde{h}_m(\boldsymbol{x}^{(i)})\right)

החסם על ה misclassification rate

נתחיל בעובדה שעבור y=±1y=\pm1 וערך כל שהוא zz מתקיים ש:

I{sign(z)≠y}=I{sign(yz)≠1}≤exp⁡(−yz)I\{\text{sign}(z)\neq y\}= I\{\text{sign}(yz)\neq 1\} \leq \exp(-yz)

ונשתמש באי השיוון הנ"ל על כל איבר בסכום בנוסחא לשגיאה האמפירית ונקבל כי:

1N∑iI{h(x(i))≠y(i)}=1N∑iI{sign(∑m=1Mαmh~m(x(i)))≠y(i)}≤1N∑i=1Nexp⁡(−∑m=1My(i)αmh~m(x(i)))\begin{aligned} \frac{1}{N}\sum_i I\{h(\boldsymbol{x}^{(i)})\neq y^{(i)}\} &=\frac{1}{N}\sum_i I\left\lbrace\text{sign}\left(\sum_{m=1}^M\alpha_m\tilde{h}_m(\boldsymbol{x}^{(i)})\right)\neq y^{(i)}\right\rbrace\\ &\leq\frac{1}{N}\sum_{i=1}^N\exp\left(-\sum_{m=1}^M y^{(i)}\alpha_m\tilde{h}_m(\boldsymbol{x}^{(i)})\right) \end{aligned}

בעיית האופטימיזציה של AdaBoost

על פי החסם שהצגנו לעיל נוכל להניח כי מזעור של בעיית האופטימיזציה הבאה:

arg⁡min⁡{αm,h~m}m=1M1N∑i=1Nexp⁡(−∑m=1Mαmy(i)h~m(x(i)))\underset{\{\alpha_m,\tilde{h}_m\}_{m=1}^M}{\arg\min}\quad \frac{1}{N}\sum_{i=1}^N\exp\left(-\sum_{m=1}^M\alpha_m y^{(i)}\tilde{h}_m(\boldsymbol{x}^{(i)})\right)

תגרום כנראה להקטנת השגיאה האמפירית ובכך להקטנת ההטיה.

  • אנו נראה בהמשך כי תחת תנאים מסויימים כאשר M→∞M\rightarrow\infty החסם ידעך ל-0.

בעיית האופטימיזציה של AdaBoost

arg⁡min⁡{αm,h~m}m=1M1N∑i=1Nexp⁡(−∑m=1Mαmy(i)h~m(x(i)))\underset{\{\alpha_m,\tilde{h}_m\}_{m=1}^M}{\arg\min}\quad \frac{1}{N}\sum_{i=1}^N\exp\left(-\sum_{m=1}^M\alpha_m y^{(i)}\tilde{h}_m(\boldsymbol{x}^{(i)})\right)
  • AdaBoost מנסה לפתור את בעיית האופטימיזציה בצורה חמדנית.
  • אנו נגדיל את MM בהדרגה כאשר בכל פעם נחפש את ה αm\alpha_m וה h~m\tilde{h}_m האופטימלים.

בעיית האופטימיזציה של AdaBoost

arg⁡min⁡{αm,h~m}m=1M1N∑i=1Nexp⁡(−∑m=1Mαmy(i)h~m(x(i)))\underset{\{\alpha_m,\tilde{h}_m\}_{m=1}^M}{\arg\min}\quad \frac{1}{N}\sum_{i=1}^N\exp\left(-\sum_{m=1}^M\alpha_m y^{(i)}\tilde{h}_m(\boldsymbol{x}^{(i)})\right)

נסתכל על המצב בו כבר מצאנו את כל ה αm\alpha_m וה h~m\tilde{h}_m עד ל M−1M-1, וכעת אנו רוצים למצוא את αM\alpha_M ו h~M\tilde{h}_M:

αM,h~M=arg⁡min⁡α,h~1N∑i=1Nexp⁡(−∑m=1M−1αmy(i)h~m(x(i))−αy(i)h~(x(i)))\alpha_M,\tilde{h}_M=\underset{\alpha,\tilde{h}}{\arg\min}\quad \frac{1}{N}\sum_{i=1}^N\exp\left(-\sum_{m=1}^{M-1}\alpha_m y^{(i)}\tilde{h}_m(\boldsymbol{x}^{(i)})-\alpha y^{(i)}\tilde{h}(\boldsymbol{x}^{(i)})\right)
  • αM\alpha_M יכול לקבל כל ערך.
  • את h~M\tilde{h}_M עלינו לבחור מתוך מאגר מסווגים נתון.

בעיית האופטימיזציה של AdaBoost

αM,h~M=arg⁡min⁡α,h~1N∑i=1Nexp⁡(−∑m=1M−1αmy(i)h~m(x(i))−αy(i)h~(x(i)))\alpha_M,\tilde{h}_M=\underset{\alpha,\tilde{h}}{\arg\min}\quad \frac{1}{N}\sum_{i=1}^N\exp\left(-\sum_{m=1}^{M-1}\alpha_m y^{(i)}\tilde{h}_m(\boldsymbol{x}^{(i)})-\alpha y^{(i)}\tilde{h}(\boldsymbol{x}^{(i)})\right)

הדרך לפתור את בעיית האופטימיזציה:

  1. רישום מחדש של בעיית האופטימיזציה בצורה יותר פשוטה.
  2. מציאת αM\alpha_M כפונקציה של h~M\tilde{h}_M על ידי גזירה והשוואה ל-0.
  3. הצבה של αM\alpha_M בחזרה לבעיית האופטימיזציה על מנת לקבל ביטוי פשוט שאותו יש למזער כתלות ב h~M\tilde{h}_M.

נציג כעת את הפתרון של בעיה זו, כאשר הפיתוח המלא של הפתרון מופיע בסוף ההרצאה.

בעיית האופטימיזציה של AdaBoost

αM,h~M=arg⁡min⁡α,h~1N∑i=1Nexp⁡(−∑m=1M−1αmy(i)h~m(x(i))−αy(i)h~(x(i)))\alpha_M,\tilde{h}_M=\underset{\alpha,\tilde{h}}{\arg\min}\quad \frac{1}{N}\sum_{i=1}^N\exp\left(-\sum_{m=1}^{M-1}\alpha_m y^{(i)}\tilde{h}_m(\boldsymbol{x}^{(i)})-\alpha y^{(i)}\tilde{h}(\boldsymbol{x}^{(i)})\right)

נגדיר את הגדלים הבאים:

w~i(M−1)=exp⁡(−∑m=1M−1αmy(i)h~m(x(i)))wi(M−1)=w~i(M−1)∑j=1Nw~j(M−1)משקל  גבוה  לדגימות  קשותε(h~,{wi})=∑i=1NwiI{y(i)≠h~(x(i))}\begin{aligned} \tilde{w}_i^{(M-1)}&=\exp\left(-\sum_{m=1}^{M-1}\alpha_m y^{(i)}\tilde{h}_m(\boldsymbol{x}^{(i)})\right)\\ w_i^{(M-1)}&=\frac{\tilde{w}_i^{(M-1)}}{\sum_{j=1}^N\tilde{w}_j^{(M-1)}} \qquad {משקל\;גבוה\;לדגימות\;קשות} \\ \varepsilon(\tilde{h},\{w_i\})&=\sum_{i=1}^N w_iI\{y^{(i)}\neq \tilde{h}(\boldsymbol{x}^{(i)})\} \end{aligned}

בעיית האופטימיזציה של AdaBoost

h~M\tilde{h}_M ו αM\alpha_M האופטימאליים בכל שלב יהיו נתונים על ידי:

h~M=arg⁡min⁡h~ ε(h~,{wi(M−1)})=arg⁡min⁡h~ ∑i=1Nwi(M−1)I{y(i)≠h~(x(i))}\tilde{h}_M =\underset{\tilde{h}}{\arg\min}\ \varepsilon(\tilde{h},\{w_i^{(M-1)}\}) =\underset{\tilde{h}}{\arg\min}\ \sum_{i=1}^N w_i^{(M-1)}I\{y^{(i)}\neq \tilde{h}(\boldsymbol{x}^{(i)})\}

ו

αM=12ln⁡(1−εMεM)\alpha_M=\frac{1}{2}\ln\left(\frac{1-\varepsilon_M}{\varepsilon_M}\right)

כאשר סימנו:

εM=ε(h~M,{wi(M−1)})\varepsilon_M=\varepsilon(\tilde{h}_M,\{w_i^{(M-1)}\})

כאשר h~M\tilde{h}_M הינו מסווג טוב לדגימות קשות. הוכחה מלאה ברשימות.

בעיית האופטימיזציה של AdaBoost

אם כן, בכל שלב עלינו לבצע את הפעולות הבאות:

  1. חישוב המשקלים {wi(M−1)}\{w_i^{(M-1)}\}.
  2. מציאת החזאי h~\tilde{h} אשר ממזער את שגיאת 0-1 האמפירית הממושקלת.
  3. חישוב המקדם αM\alpha_M.

בפועל ניתן לחשב את המשקלים של ה צעד ה MM כבר בסוף הצעד ה M−1M-1. בנוסף ניתן להשתמש בעובדה ש:

w~i(M)=w~i(M−1)exp⁡(−αMy(i)h~M(x(i)))\tilde{w}_i^{(M)}=\tilde{w}_i^{(M-1)}\exp\left(-\alpha_M y^{(i)}\tilde{h}_M(\boldsymbol{x}^{(i)})\right)

כדי להימנע מלחשב את הסכום על mm ולקצר את החישוב.

האלגוריתם של AdaBoost

נאתחל את המשקולות wi(0)=1Nw_i^{(0)}=\frac{1}{N}.

  1. נבחר את המסווג אשר ממזער את:

    h~M=arg⁡min⁡h~ ∑i=1Nwi(M−1)I{y(i)≠h~(x(i))}\tilde{h}_M=\underset{\tilde{h}}{\arg\min}\ \sum_{i=1}^N w_i^{(M-1)}I\{y^{(i)}\neq \tilde{h}(\boldsymbol{x}^{(i)})\}

  2. נחשב את המקדם αM\alpha_{M} של המסווג:

    εM=∑i=1Nwi(M−1)I{y(i)≠h~M(x(i))}αM=12ln⁡(1−εMεM)\begin{aligned} \varepsilon_M&=\sum_{i=1}^N w_i^{(M-1)}I\{y^{(i)}\neq \tilde{h}_{M}(\boldsymbol{x}^{(i)})\}\\ \alpha_M&=\frac{1}{2}\ln\left(\frac{1-\varepsilon_M}{\varepsilon_M}\right) \end{aligned}

האלגוריתם של AdaBoost

  1. נעדכן את וקטור המשקלים:

    w~i(M)=wi(M−1)exp⁡(−αMy(i)h~M(x(i)))wi(M)=w~i(M)∑j=1Nw~j(M)\begin{aligned} \tilde{w}_i^{(M)}&=w_i^{(M-1)}\exp\left(-\alpha_M y^{(i)}\tilde{h}_M(\boldsymbol{x}^{(i)})\right)\\ w_i^{(M)}&=\frac{\tilde{w}_i^{(M)}}{\sum_{j=1}^N \tilde{w}_j^{(M)}} \end{aligned}

המשמעות של המשקלים

המשקל ללא הנרמול של הדגימה ה ii שווה ל:

w~i(M)=exp⁡(−y(i)∑m=1Mαmh~m(x(i)))\tilde{w}_i^{(M)}=\exp\left(-y^{(i)}\sum_{m=1}^{M}\alpha_m\tilde{h}_m(\boldsymbol{x}^{(i)})\right)
  • משקל זה מציין עד כמה טוב האלגוריתם מסווג את הדגימה ה ii.
  • דגימות שלא מסווגות נכון יהיו בעלות משקל גדול.
  • התפקיד של המשקלים הוא לדאוג שהאלגוריתם יבחר בכל צעד את החזאי אשר ישפר את הסיווג בעיקר על הדגימות שעליהן החזאי הנוכחי טועה.

תנאי עצירה

  • בחלק גדול מהמקרים AdaBoost ילך ויקטין את שגיאת החיזוי על המדגם עד שהוא יגיע לסיווג מושלם.
  • AdaBoost ממשיך לשפר את יכולת ההכללה שלהו גם אחרי שהוא הגיע לסיווג מושלם.
  • כמות התאמת היתר גדלה בקצב מאד איטי (אם בכלל).
  • נרצה להריץ את האלגוריתם מספר רב של צעדים ולבדוק את הביצועים על validation set.

Before training

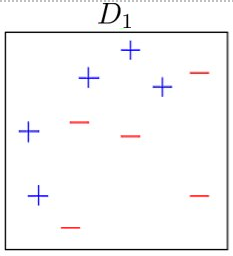
Round 1

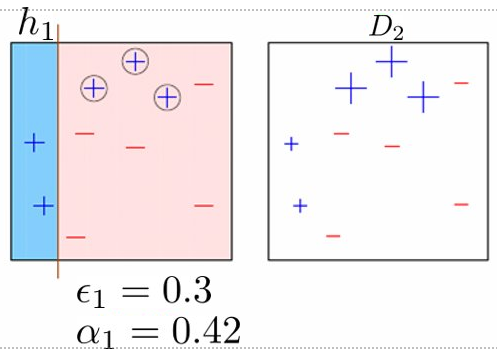
Round 2

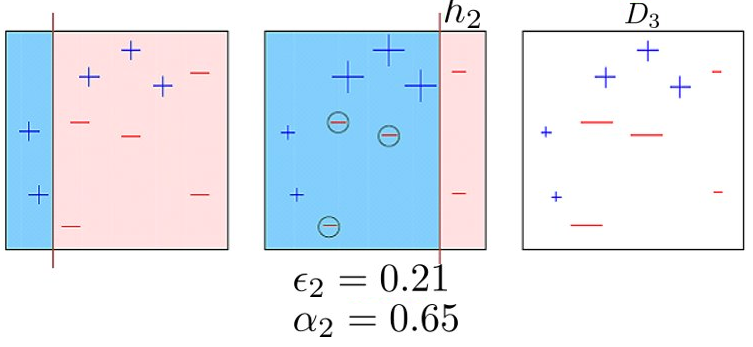
Round 3

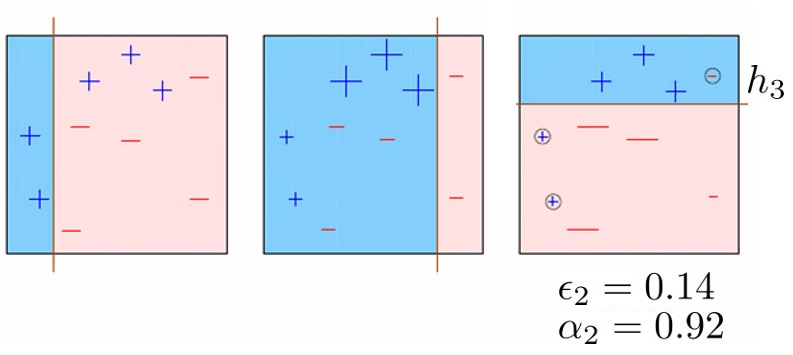
Final

קצב ההתכנסות של החסם

ראינו קודם כי שגיאת 0-1 האמפירית (הלא ממושקלת) של החזאי על המדגם חסומה על ידי הביטוי:

1N∑iI{h(x(i))≠y(i)}≤1N∑i=1Nexp⁡(−∑m=1My(i)αmh~m(x(i)))\frac{1}{N}\sum_i I\{h(\boldsymbol{x}^{(i)})\neq y^{(i)}\} \leq\frac{1}{N}\sum_{i=1}^N\exp\left(-\sum_{m=1}^M y^{(i)}\alpha_m\tilde{h}_m(\boldsymbol{x}^{(i)})\right)

נראה כעת כי תחת תנאים מסויימים מובטח כי חסם זה ידעך ל-0 ככל שנגדיל את MM.

טענה (הוכחה מלאה ברשימות)

נסמן את שגיאת 0-1 האמפירית הממושקלת בצעד ה mm ב εm=12−γm\varepsilon_m=\frac{1}{2}-\gamma_m. נטען כי מתקיים הקשר הבא:

1N∑i=1Nexp⁡(−∑m=1My(i)αmh~m(x(i)))≤exp⁡(−2∑m=1Mγm2)\frac{1}{N}\sum_{i=1}^N\exp\left(-\sum_{m=1}^M y^{(i)}\alpha_m\tilde{h}_m(\boldsymbol{x}^{(i)})\right) \leq\exp\left(-2\sum_{m=1}^M\gamma_m^2\right)

מכאן שבמידה וקיים γ\gamma אשר מקיים γm≥γ>0\gamma_m\geq\gamma>0 אזי מתקיים ש:

1N∑iI{h(x(i))≠y(i)}≤1N∑i=1Nexp⁡(−∑m=1My(i)αmh~m(x(i)))≤exp⁡(−2Mγ2)\begin{aligned} &\frac{1}{N}\sum_i I\{h(\boldsymbol{x}^{(i)})\neq y^{(i)}\} \\ &\qquad \leq\frac{1}{N}\sum_{i=1}^N\exp\left(-\sum_{m=1}^M y^{(i)}\alpha_m\tilde{h}_m(\boldsymbol{x}^{(i)})\right) \leq\exp\left(-2M\gamma^2\right) \end{aligned}

זאת אומרת, שקיים חסם לשגיאת 0-1 האמפירית אשר דועך באופן מעריכי עם MM.

יתרונות

  • הקטנת ההטיה
  • מימוש פשוט ויעיל
  • ניתן לשימוש עם מגוון מסווגים בסיסיים

חסרונות

  • התאמת יתר ורגישות לרעש (התמקדות בדוגמאות קשות)
  • קשה למימוש מקבילי
  • רגישות לבחירה של מסווגי בסיס
  • פרשנות מורכבת (למשל, ביחס לעצי החלטה)

הרחבות

  • רבות ומגוונות. בחלקו משלבות רגולריזציה, אפשרות לעיבוד מקבילי, שילוב עם bagging ועוד