הרצאה 4 - סיווג דיסקרימינטיבי

מה נלמד היום

בעיות סיווג

בעיות supervised learning שבהם $\text{y}$ משתנה אקראי בדיד אשר יכול לקבל סט ערכים סופי (לרוב קטן).

דוגמאות לבעיות סיווג:

• מערכת להתראה על מכשולים בכביש (הולך רגל, קרבה לרכב שמלפנים וכו') מתוך תמונות ממצלמת דרך.
• מערכת לסינון דואר זבל.
• מערכת לזיהוי כתב יד בתמונה.
• מערכות speech-to-text אשר הופכות קטע אודיו למילים.
• מערכת לזיהוי פנים בתמונות.

ההבדל מבעיות רגרסיה

• החזאי ייצר ערכים בדידים ולכן:

  • לא נוכל להשתמש במודלים רציפים כפי שהם.
  • אין נגזרת ולכן לא נוכל לגזור ולהשוות ל-0 או להשתמש ב gradient descent.
• לרוב לא תהיה משמעות למרחק בין $\hat{y}$ ל $y$, לכן לא רלוונטי להשתמש בפונקציות מחיר כמו MSE אשר מתייחסות לגודל שגיאת החיזוי.

גישה דיסקרימינטיבית - תזכורת

• אנו מנסים לבנות חזאי בעל ביצועים טובים ככל האפשר על המדגם.
• כדי ולהגביל את התאמת היתר (overfitting) אנו נשים מגבלות על פונקציית החיזוי.

בהרצאה הקרובה נכיר שתי שיטות דיסקרימינטיביות לפתרון בעיות סיווג.

בעיה לדוגמא - זיהוי הונאות בכרטיסי אשראי

נסיון לסווג עסקאות כחשודות בהונאה על סמך פרטי העסקה:

• הסכום.
• מרחק העיסקה (נניח המיקום של החנות) מהעיסקה האחרונה.
• מרחק העיסקה מהכתובת של הלקוח.
• השעה ביום.
• אופי המוצרים שהחנות מוכרת (מכולת, מוצרי חשמל, ביגוד, רכב, נדל"ן, וכו')

ניתן לעשות זאת בעזרת supervised learning על ידי שימוש במדגם דוגמאות מהעבר.

בעיה לדוגמא - המדגם

בהרצאה זו נשתמש בעיה זו כדוגמא. נתייחס למדגם הבא:

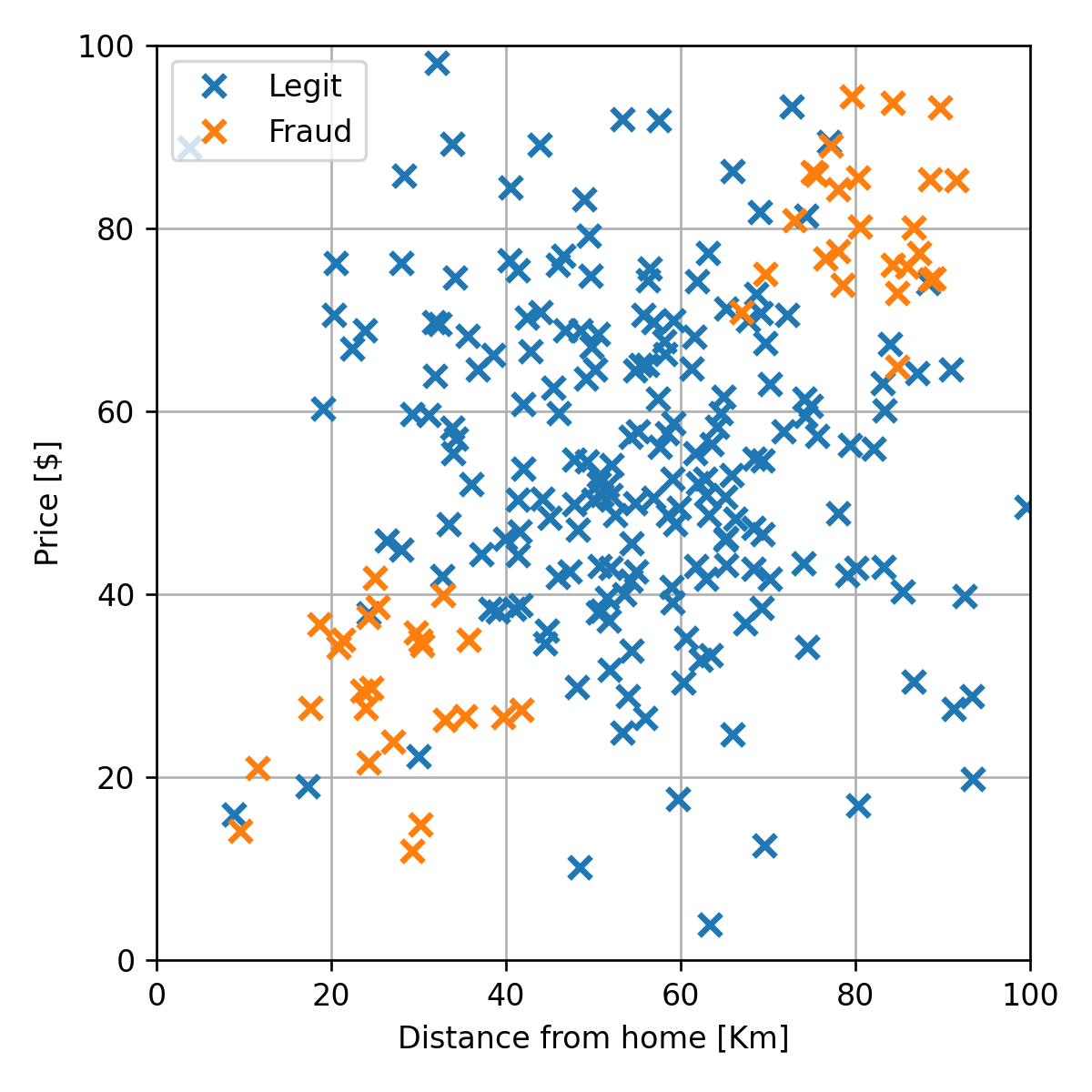
בעיה לדוגמא - החזאי

נרצה למצוא חזאי אשר יחזה עיסקאות חשודות על פי מרחק ומחיר. לדוגמא:

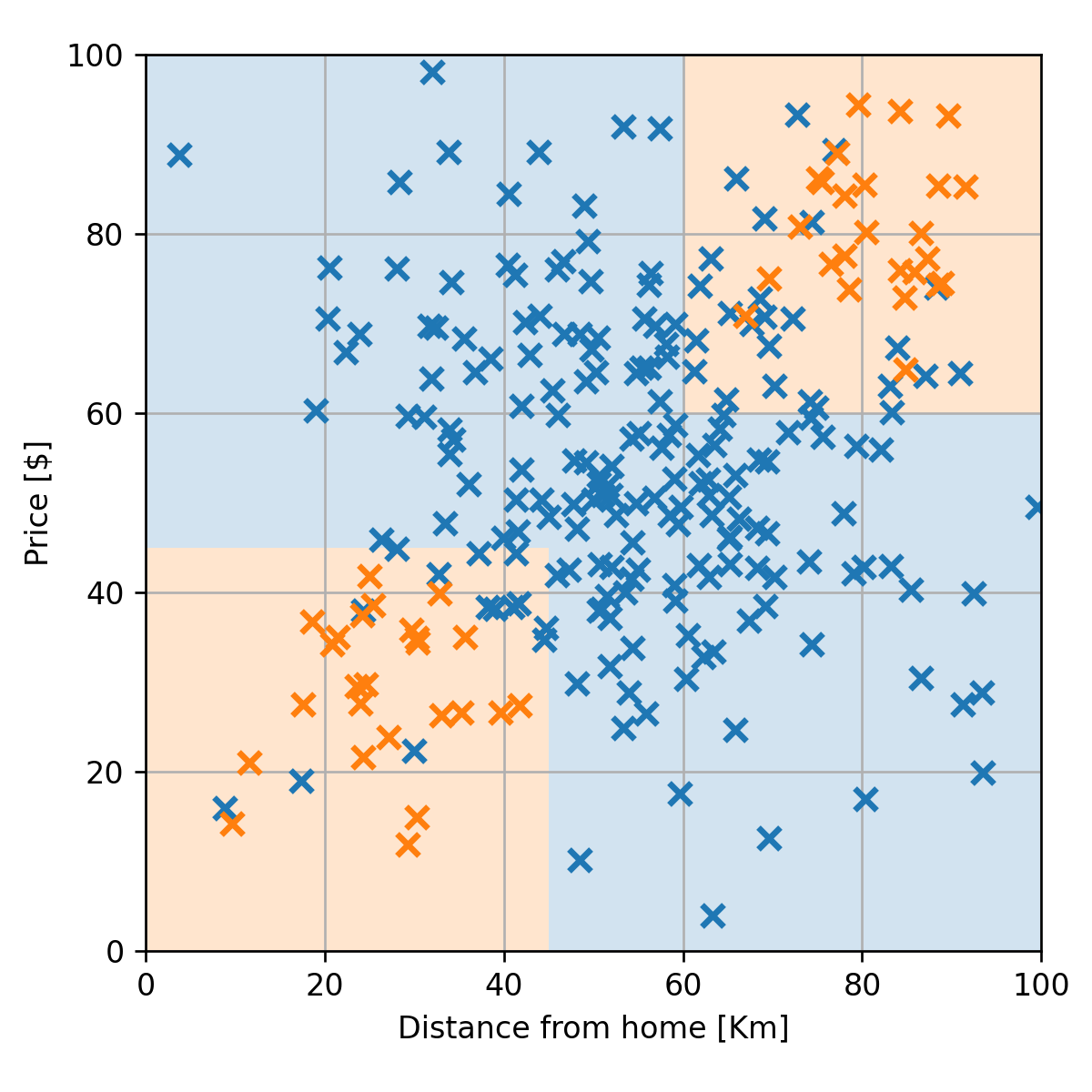
חלוקה ל train-test

נחלק את המדגם ל80% train ו 20% test:

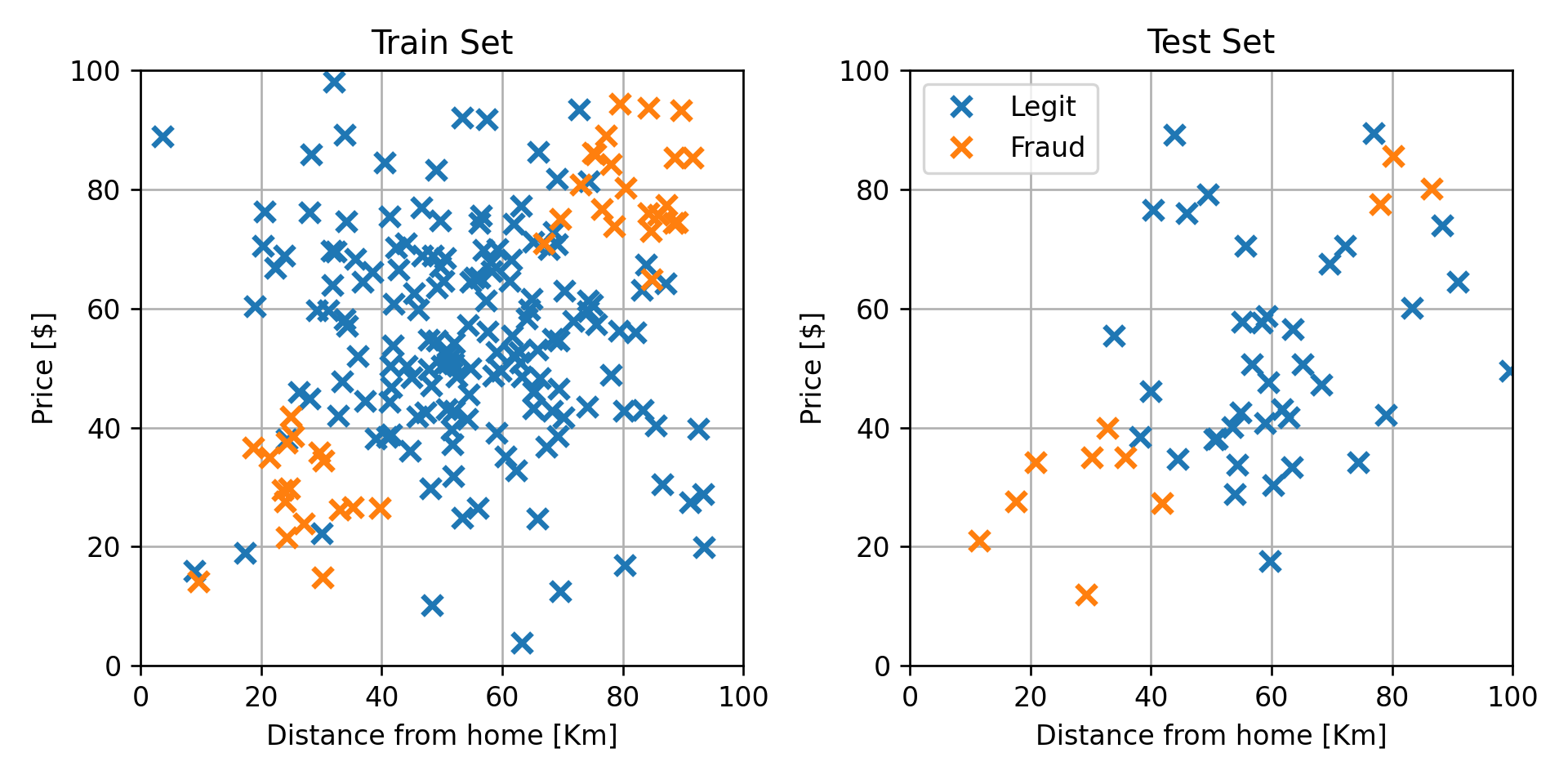
שמות וסימונים בבעיות סיווג

• חזאי = מסווג (classifier) = discriminator (מקטלג).
• מחלקות - הערכים השונים שאותם התוויות יכול לקבל.
• $C$ - מספר המחלקות.
• סיווג בינארי - בעיות בהם $C=2$.

• סימון המחלקות בסיווג בינארי:

  • $y\in\{0,1\}$ או $y\in\{-1,1\}$.

• סימון המחלקות בסיווג לא בינארי:

  • $y\in\{1,2,\dots,C\}$ או $y\in\{0,1,\dots,C-1\}$.

Misclassification rate - תזכורת

שאלה: מתי פונקציה כזו אינה סבירה?

• פונקציית המחיר הנפוצה בבעיות סיווג.
• מחשבת את התדירות שבה צפוי החזאי לבצע שגיאות חיזוי (ללא קשר לגודל השגיאה).

• פונקציית risk עם zero-one-loss:

  $$l(\hat{y},y)=I\{\hat{y}\neq y\}$$

החזאי האופטימאלי של miscalssification

בהינתן הפילוג המשותף של $\mathbf{x}$ ו $\text{y}$ ניתן לחשב את החזאי האופטימאלי:

• מחזיר את ה $\text{y}$ הכי סביר (הכי שכיח, ה mode) בהסתברות של $\text{y}$ בהינתן $\mathbf{x}$.

נקרא גם: "מסווג בייס" (Bayes Classifier).

אלגוריתם סיווג המבצע חיזוי על סמך השכן הכי קרוב במדגם:

נתון מדגם $\mathcal{D}=\{\boldsymbol{x}^{(i)},y^{(i)}\}$ ודגימה נוספת $\boldsymbol{x}$ (אשר אינה חלק מהמדגם) שעליה נרצה לבצע את החיזוי. נבצע חיזוי בשיטת ה 1-NN באופן הבא:

1. נמצא את האינדקס של השכן הקרוב $i=\underset{i}{\arg\min} \lVert \boldsymbol{x}^{(i)}-\boldsymbol{x}\rVert_2$
2. החיזוי יהיה התווית של השכן הקרוב ביותר $\hat{y}=y^{(i)}$

שאלה: איך שונה שיטת סיווג זו משיטות קודמות שדיברנו עליהן?

הערה: ניתן להחליף את המרחק האוקילידי (נורמת $l_2$) בממדי מרחק אחרים.

דוגמא

נפעיל את 1-NN על הדוגמא שלנו:

1-NN עושה התאמת יתר

• חיזוי מושלם על הנקודות מהמדגם.
• יוצר איים סביב נקודות בודדות שכנראה מתאימות רק למדגם הספציפי.

Voronoi Cells

• החזאי מורכב מאוסף של איזורים המכונים Voronoi cells המשוייכים לכל דגימה. לכן סיבוכיות החזאי גדלה עם מספר הדוגמאות.
• איזור שבו החיזוי שהוא שהעיסקה חשודה מורכב מאוסף כל התאים של הדגימות של עסקאות חשודות.

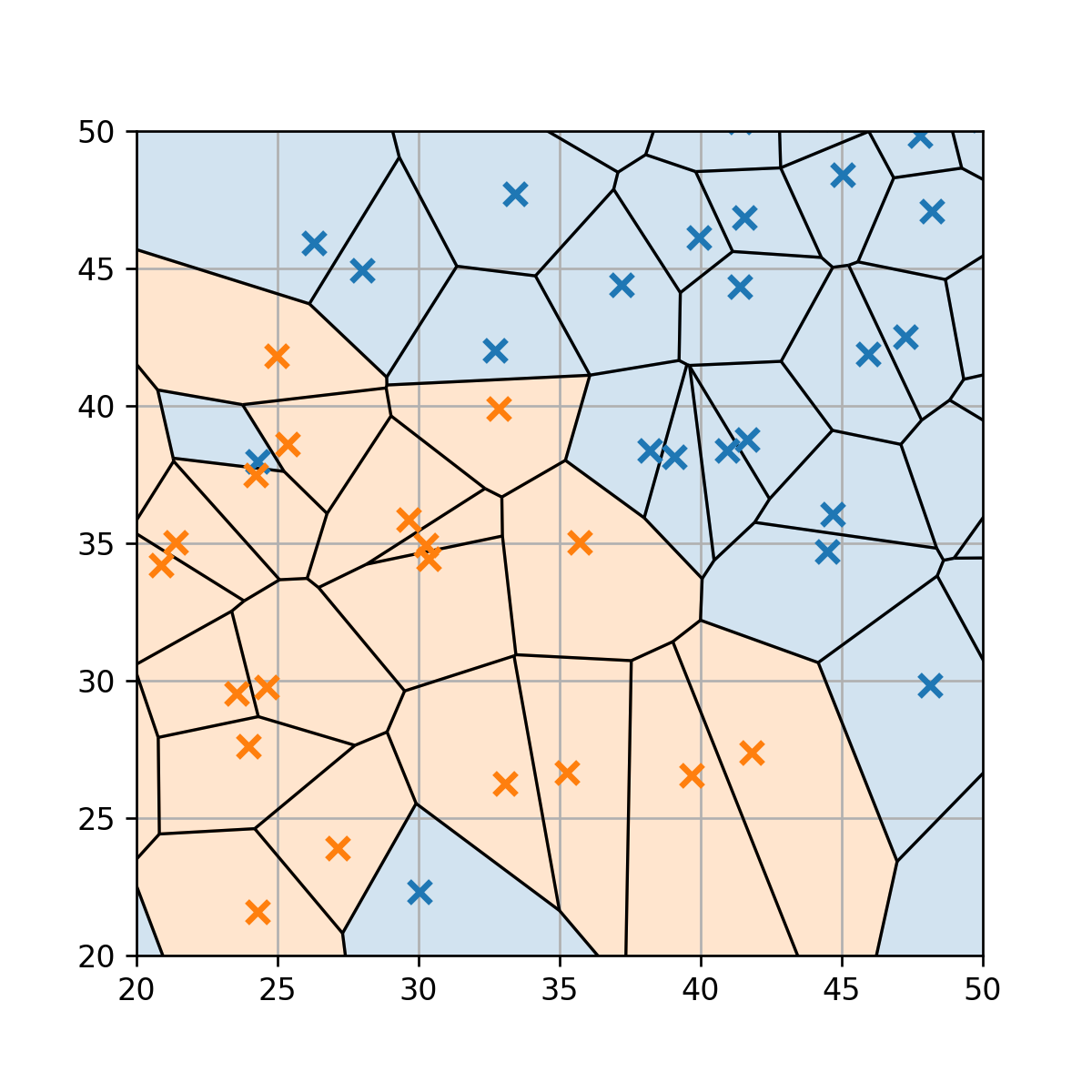
הערכת ביצועים

נבדוק את ביצועי החזאי על ה test set לפי פונקציית ה miscalssification rate:

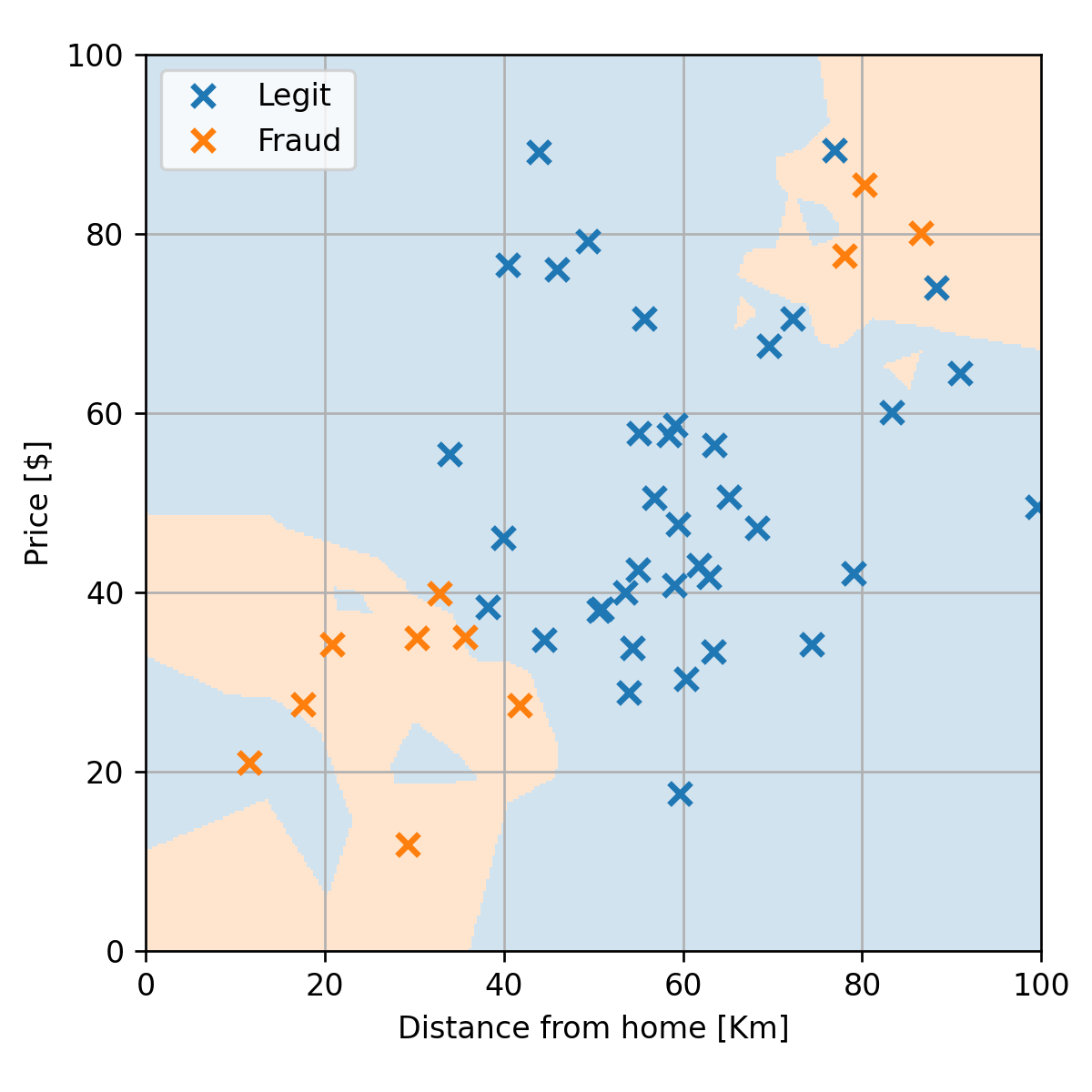
התלות ביחידות של $\mathbf{x}$

• האלגוריתם תלוי במרחקים בין נקודות ולכן ישנה חשיבות ליחידות, או יותר נכון לסדר הגדול, של הרכיבים של $\boldsymbol{x}$.
• רכיבים בעלי גודל אופייני גדול יותר יקבלו משקל גדול יותר.
• באלגוריתם זה יש לדאוג שהרכיבים של $\boldsymbol{x}$ יהיו בערך באותו סדר גודל.

לדוגמא אם היינו מודדים את המרחק במטרים:

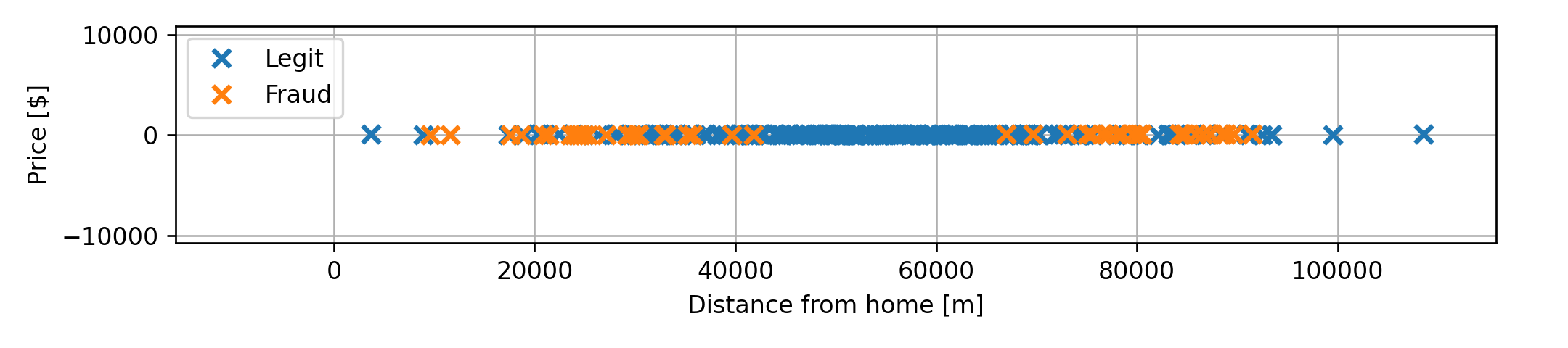
K-NN

שיפור של 1-NN על ידי שימוש במספר שכנים.

1. נמצא את $K$ השכנים בעלי ה $\boldsymbol{x}^{(i)}$ הקרובים ביותר ל $\boldsymbol{x}$.
2. תוצאת החיזוי תהיה התווית השכיחה ביותר (majority vote) מבין $K$ התוויות של הדגימות שנבחרו בשלב 1.

במקרה של שיוויון בשלב 2:

• נשווה גם את המרחק הממוצע בין ה $\boldsymbol{x}$-ים של כל תווית ונבחר לפי הקבוצה עם המרחק הממוצע הקצר ביותר.
• במקרה של שיווון גם בין המרחקים הממוצעים, נבחר אקראית.

דוגמא - 5-NN

• כמות האיים הצטמצמה.
• הגבולות בין האיזורים נעשו יותר חלקים.

הערכת ביצועים

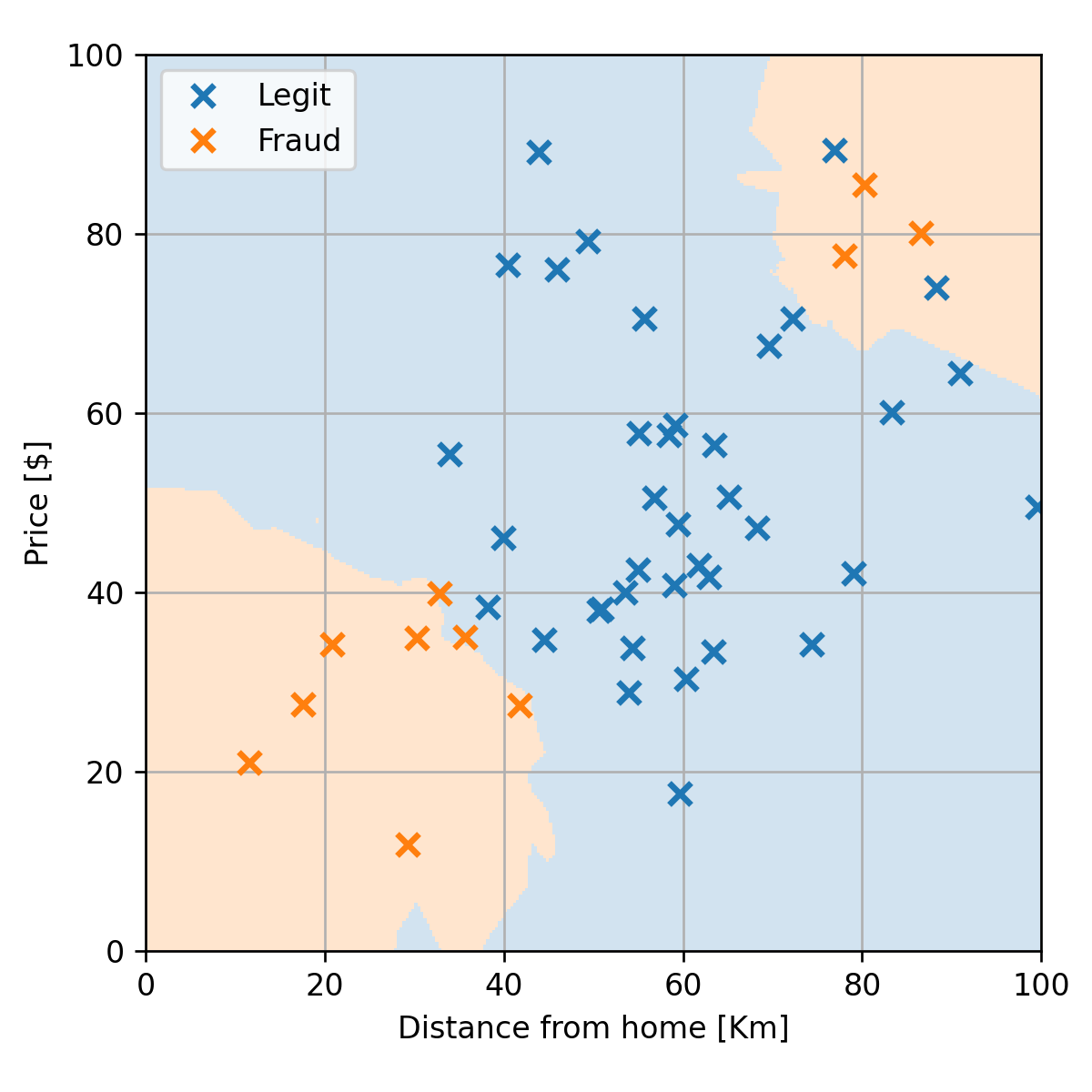
הורדנו את תדירות השגיאות ל10%.

בחירת ה $K$ האופטימאלי

נחלק את ה train set ל 75% train ו 25% validation:

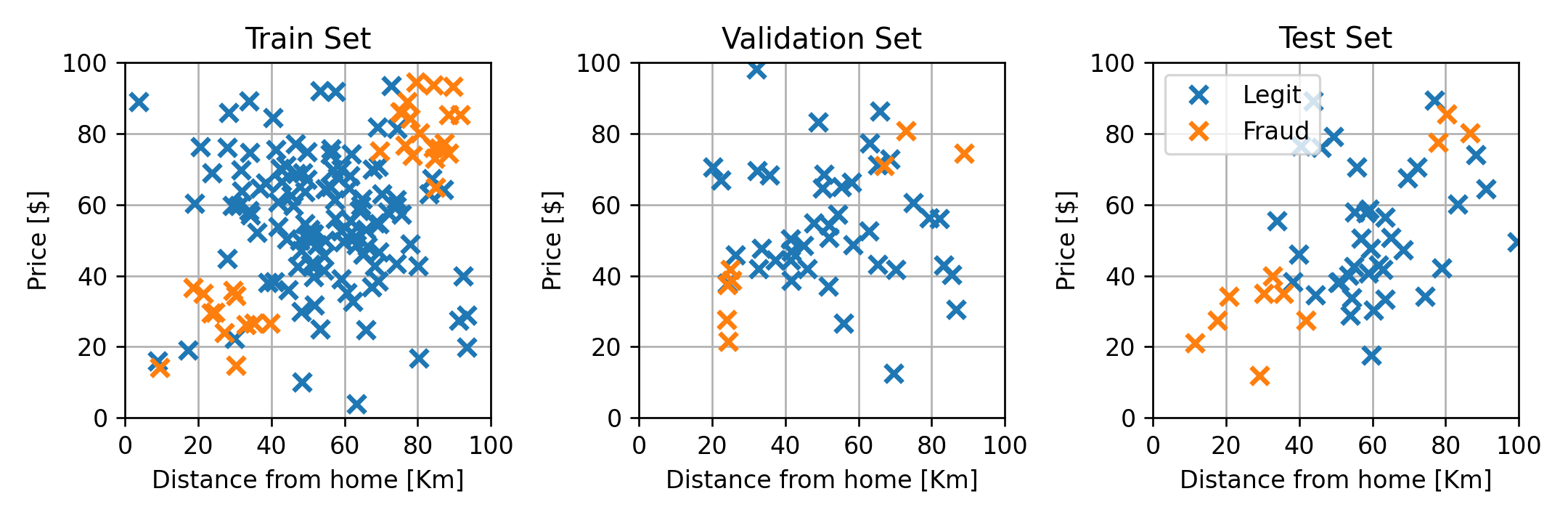
בחירת ה $K$ האופטימאלי

נחשב את הביצועים לכל $K$ על ה validation set:

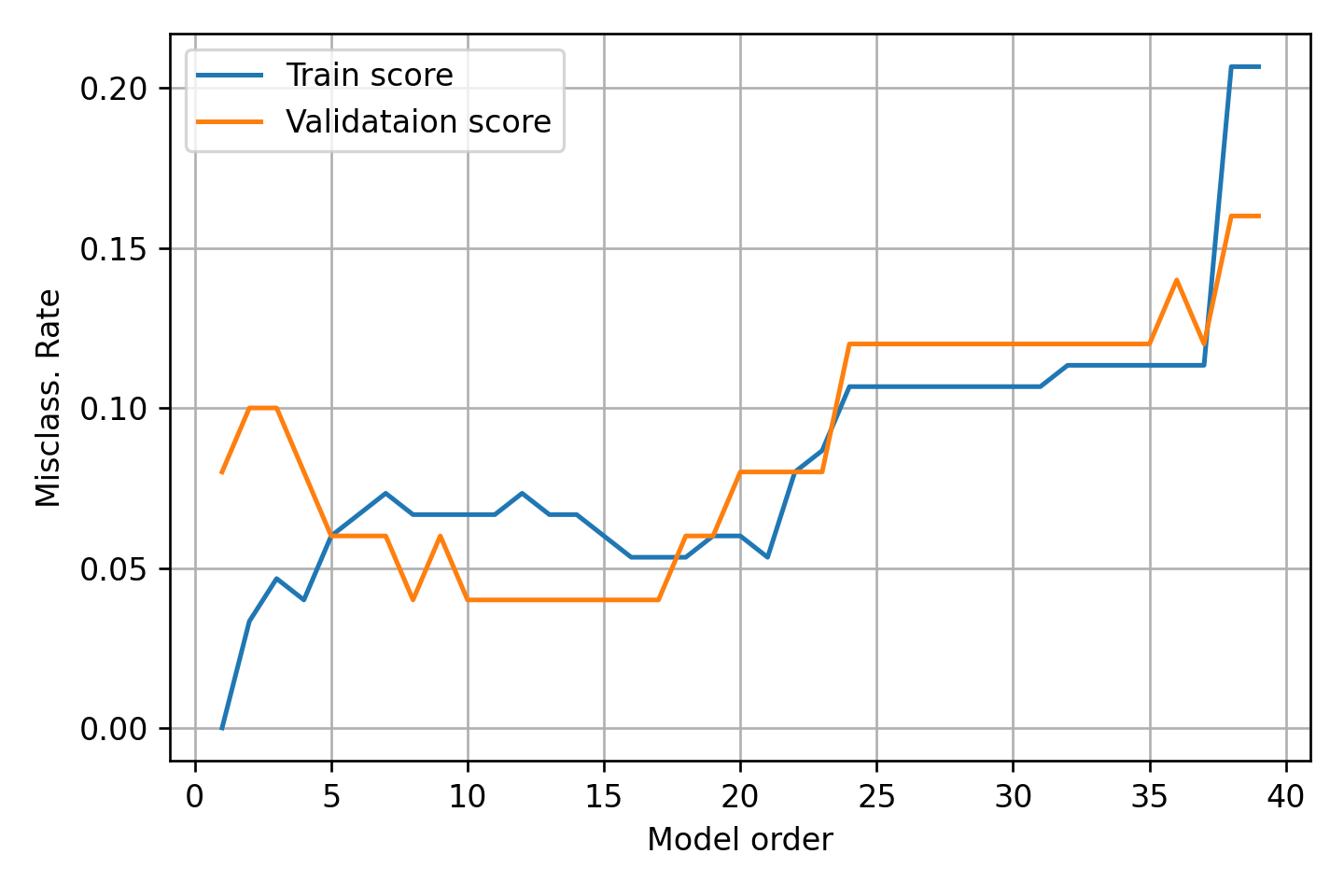
בחירת ה $K$ האופטימאלי

• זהו שוב ה bias-variance tradeoff (רק הפוך).
• בעבור 1-NN ישנה כמות גבוהה של התאמת יתר (ה train score יורד ל0).
• ככל שנגדיל את $K$ נמצע על איזור גדול יותר.
• מנקודה מסויימת יהיה רק איזור החלטה 1.

40-NN

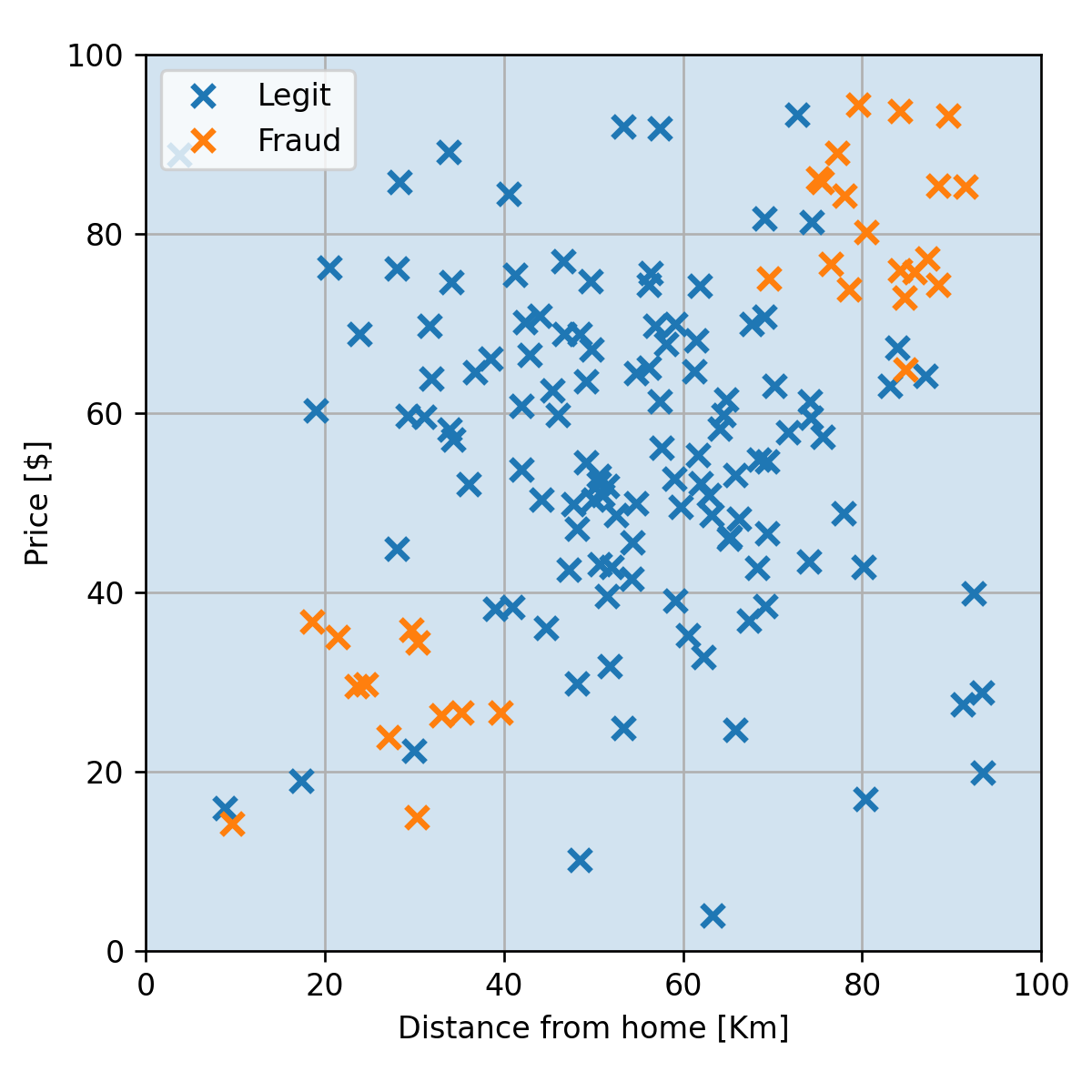
• כמובן מקרה קיצוני של underfitting.
• החזאי מתאים למדגם רק באופן מאד גס וניתן עוד לשפר את החיזוי על ידי בחירת חזאי יותר מתאים למדגם.

K-NN לבעיות רגרסיה

• ניתן להשתמש ב K-NN גם לפתרון בעיות רגרסיה, אם כי פתרון זה יהיה לרוב פחות יעיל.
• בבעיות רגרסיה אנו נבצע את החיזוי לפי הממוצע על התוויות של השכנים (במקום לבחור את תווית השכיחה).

Decision trees (עצי החלטה)

• כלי נפוץ לקבלת החלטות.
• מופיעים גם מחוץ לתחום של מערכות לומדות.

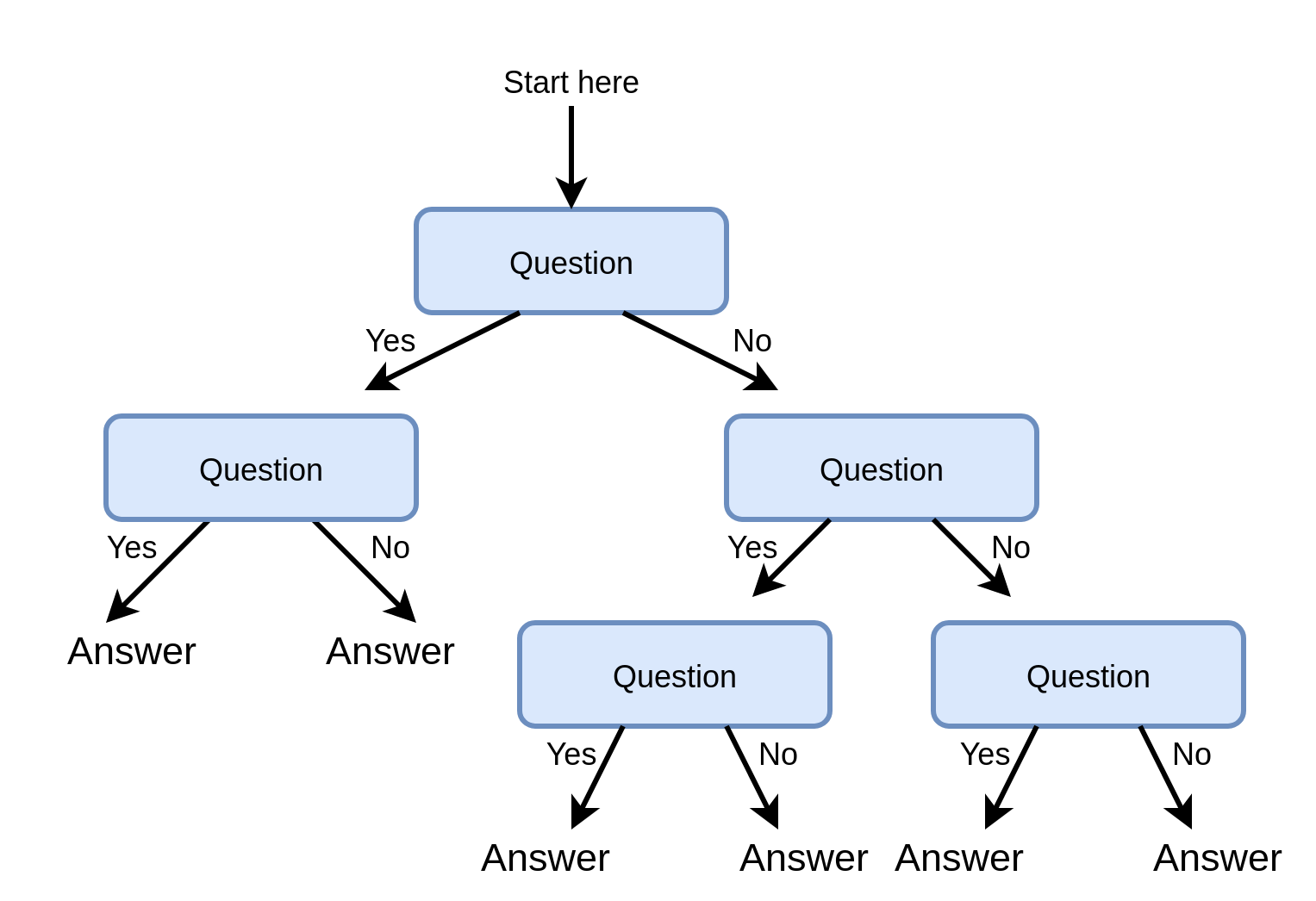
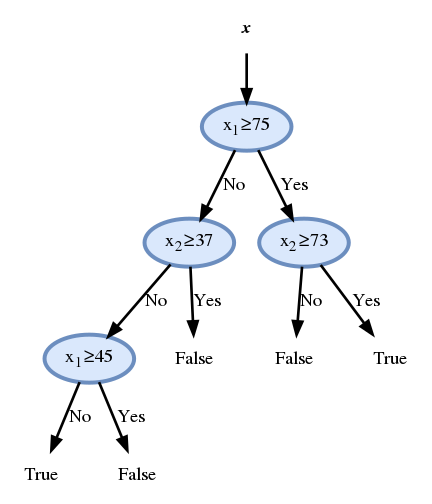
דוגמא לעץ החלטה

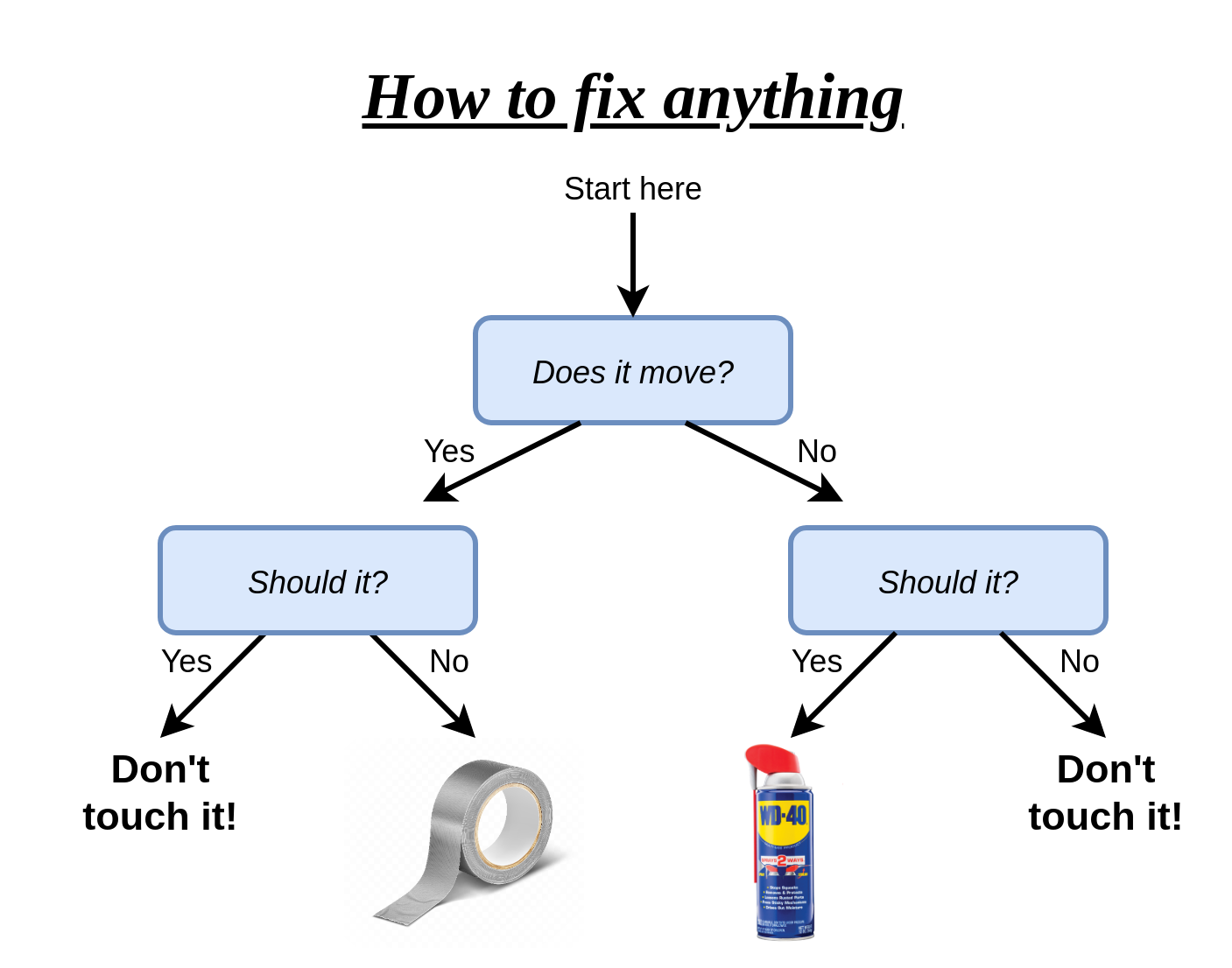
עצי החלטה ב supervised learning

נשתמש בעץ החלטה כחזאי.

יתרונות:

1. פשוט למימוש (אוסף של תנאי if .. else ..).
2. מתאים לעבודה עם משתנים קטגוריים (רכיבים של $\mathbf{x}$ שהם משתנים בדידים אשר מקבלים אחד מסט מצומצם של ערכים).
3. Explainable - ניתן להבין בדיוק מה היו השיקולים שלפיהם התקבל חיזוי מסויים.

טרמינולוגיה

• Root (שורש) - נקודת הכניסה לעץ.
• Node (צומת) - נקודות ההחלטה / פיצול של העץ - השאלות.
• Leaves (עלים) - הקצוות של העץ - התשובות.
• Branch (ענף) - חלק מתוך העץ המלא (תת-עץ).
• Depth (עומק) - מספר הצמתים במסלול הארוך ביותר.

הצמתים

לשם השמירה על הפשטות של העץ מקובל להגביל את השאלות בצמתים לתנאים פשוטים על רכיב בודד של $\mathbf{x}$:

• עבור רכיבים רציפים: נשתמש בתנאי מהצורה של $x_i>a$.
• עבור רכיבים קטגוריים: נפצל לכל אחד מהערכים שאותם יכול המשתנה לקבל.

דוגמא

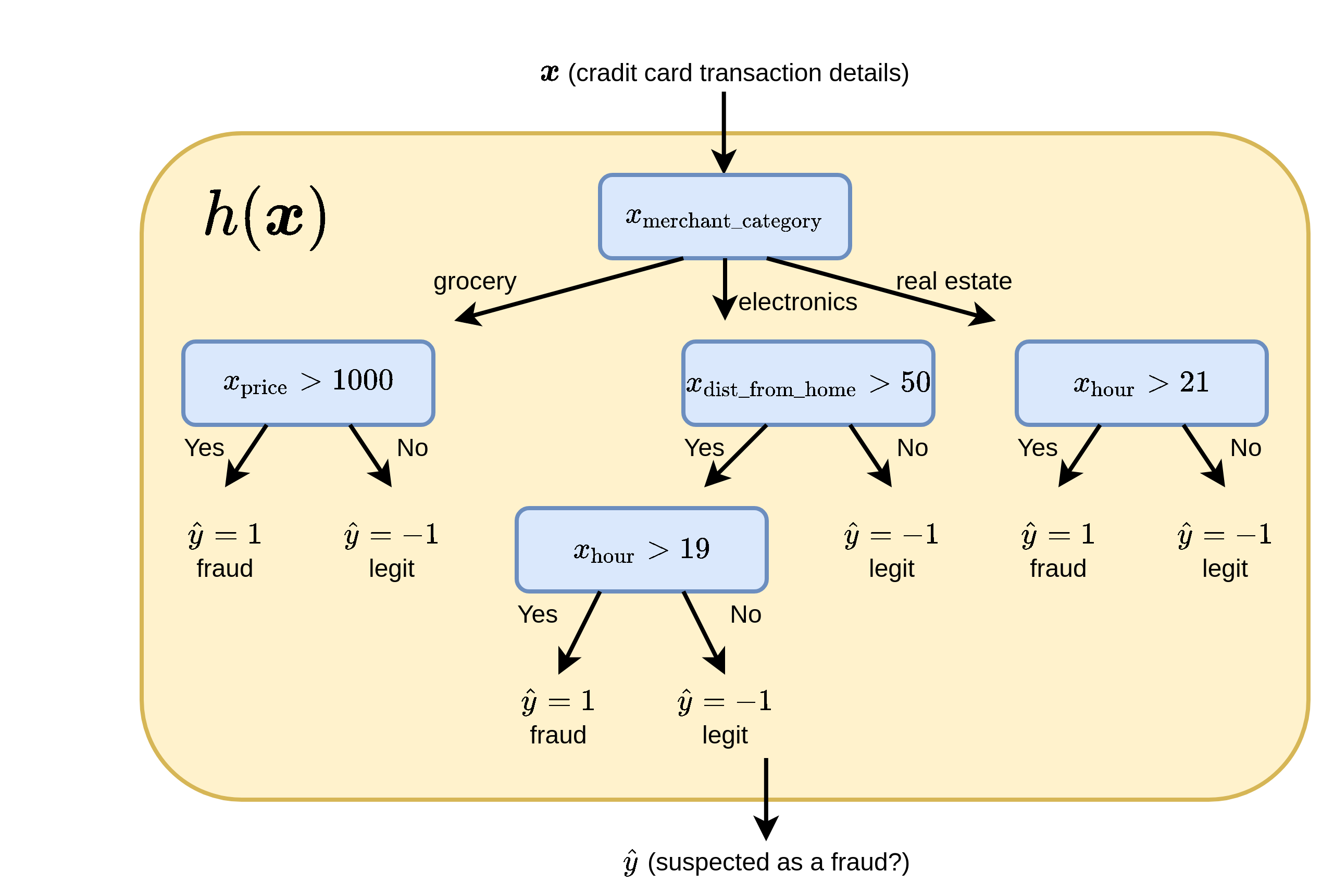
הפיצול הראשון בעץ הוא קטגורי לפי סוג המוצר ושאר הפיצולים הם לפי השוואה לסף מסויים.

בניית עץ החלטה לסיווג

• ככל שנגדיל את כמות הצמתים תגדל יכולת הביטוי ונוכל להקטין את שגיאת החיזוי על המדגם.
• ככל שנגדיל את כמות הצמתים תגדל יכולת הביטוי וכך תגדל גם כמות התאמת היתר.
• דרך אחת למניעת התאמת יתר הינה להגביל את כמות הצמתים.
• במקרים רבים אנו נרצה להגביל את הכמות הצמתים גם משיקולים מעשיים של חישוביות וזיכרון.

המטרה: לבנות עץ אשר מקטין את שגיאת החיזוי תוך שימוש בכמה שפחות צמתים.

בניית עץ החלטה לסיווג

• ישנם אלגוריתמים רבים לבניה של עץ החלטה. שני האלגוריתמים הנפוצים ביותר הם

  C4.5 (Ross Quinlan, 1986) ו CART (Breiman et al., 1984).

• בקורס זה נתאר גירסה אשר מערבת בין שניהם.
• קיימות גם הרבה גרסאות לבניית עצי החלטה אשר מבוססות על שיטות אלו.

בניית עץ החלטה לסיווג

נבנה את העץ בשני שלבים:

1. גידול העץ: ננסה לבנות עץ אשר מגיע לחיזוי הטוב ביותר שניתן על train set.
2. גיזום (pruning): נשתמש ב validation set על מנת להסיר צמתים.

שלב 1: גידול העץ

• מציאת העץ אשר מגיע לחיזוי האופטימאלי בכמה שפחות רמות דורש לעבור על כל העצים האפשריים וזה לא מעשי.
• ננסה לבנות את העץ בצורה חמדנית (greedy).
• נתחיל מהשורש ונוסיף צמתים שנותנים את שגיאת החיזוי הקטנה ביותר על ה train set.

דוגמא

נתחיל מהצומת הראשון:

דוגמא

נחפש את התנאי האידאלי על ידי מעבר על כל הרכיבים של $\boldsymbol{x}$ עם כל הספים האפשריים.

הספים האפשריים

כדי להבין מהם ערכי הסף שעליהם נרצה לעבור נסתכל לרגע על סידרת המספרים הבאה:

את סדרת המספרים הזו ניתן לפצל (על פי ערך סף) ל 2 פיצולים אפשריים על ידי:

• העברת סף בין ה 3 ל 5
• העברת סף בין ה 5 ל 8

לכן מספיק לבחון את:

• $x\geq 5$
• $x\geq 8$

מציאת הפיצול האופטימאלי

נבדוק את כל הפיצולים האפשריים

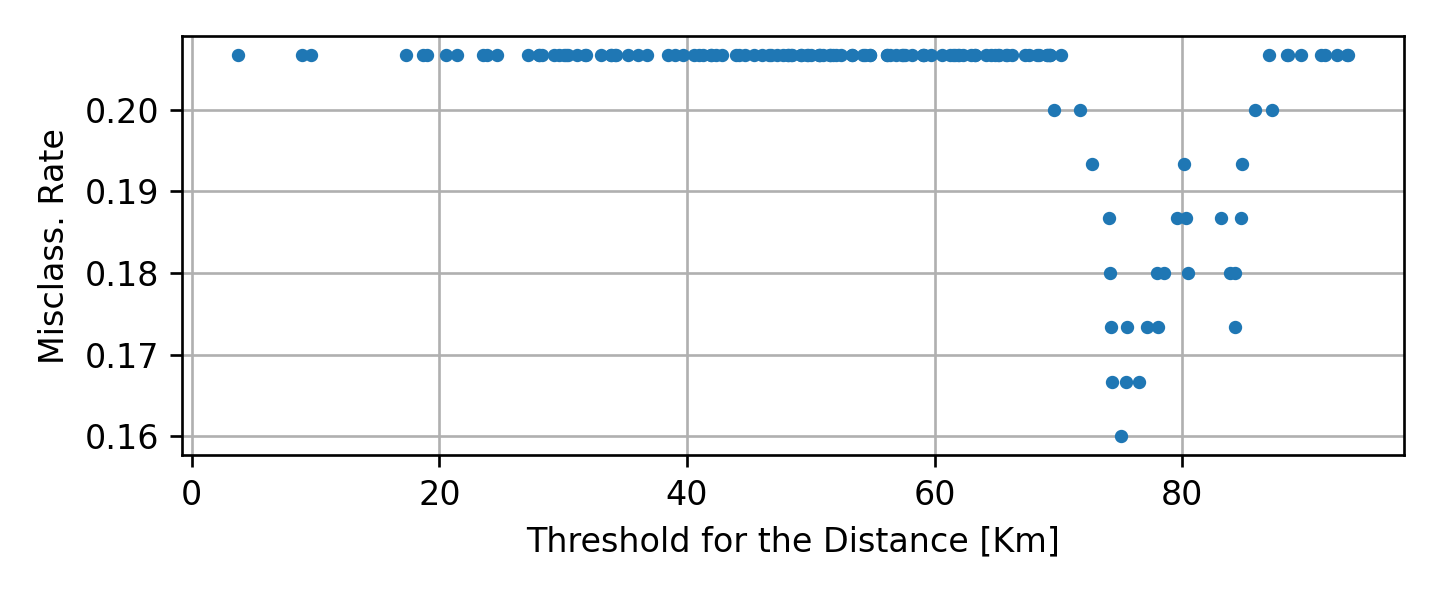
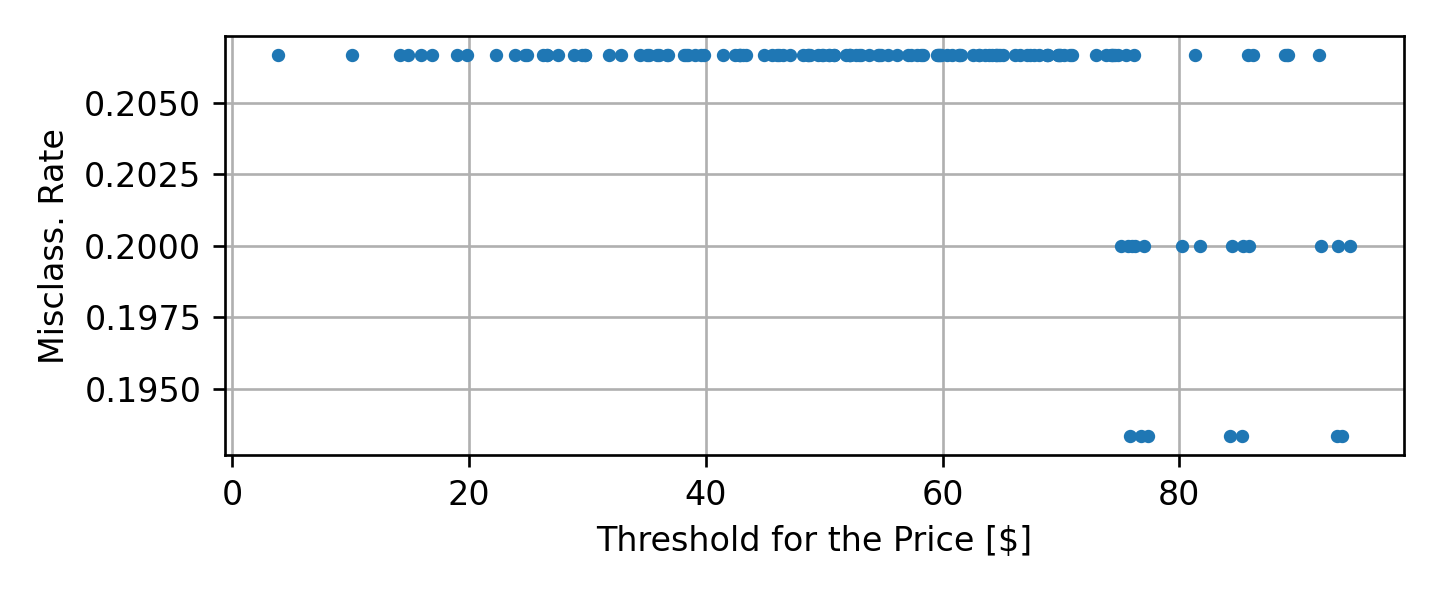
התוצאה הטובה ביותר (0.16) מתקבל בעבור $x_{\text{Distance}}\geq 75$.

הצומת הראשון

ולכן נבחר את הצומת להיות:

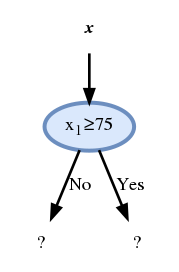
• לעלה השמאלי מגיעות 13 דגימות של הונאה ו 108 חוקיות. לכן נדרוש שהחיזוי יהיה שהעסקה חוקית.
• לעלה הימני מגיעות 18 דגימות של הונאה ו 11 חוקיות. לכן נדרוש שהחיזוי יהיה שהעסקה חשודה כהונאה.

הצומת הראשון

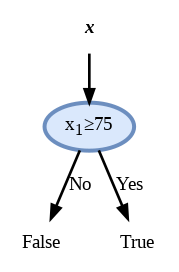
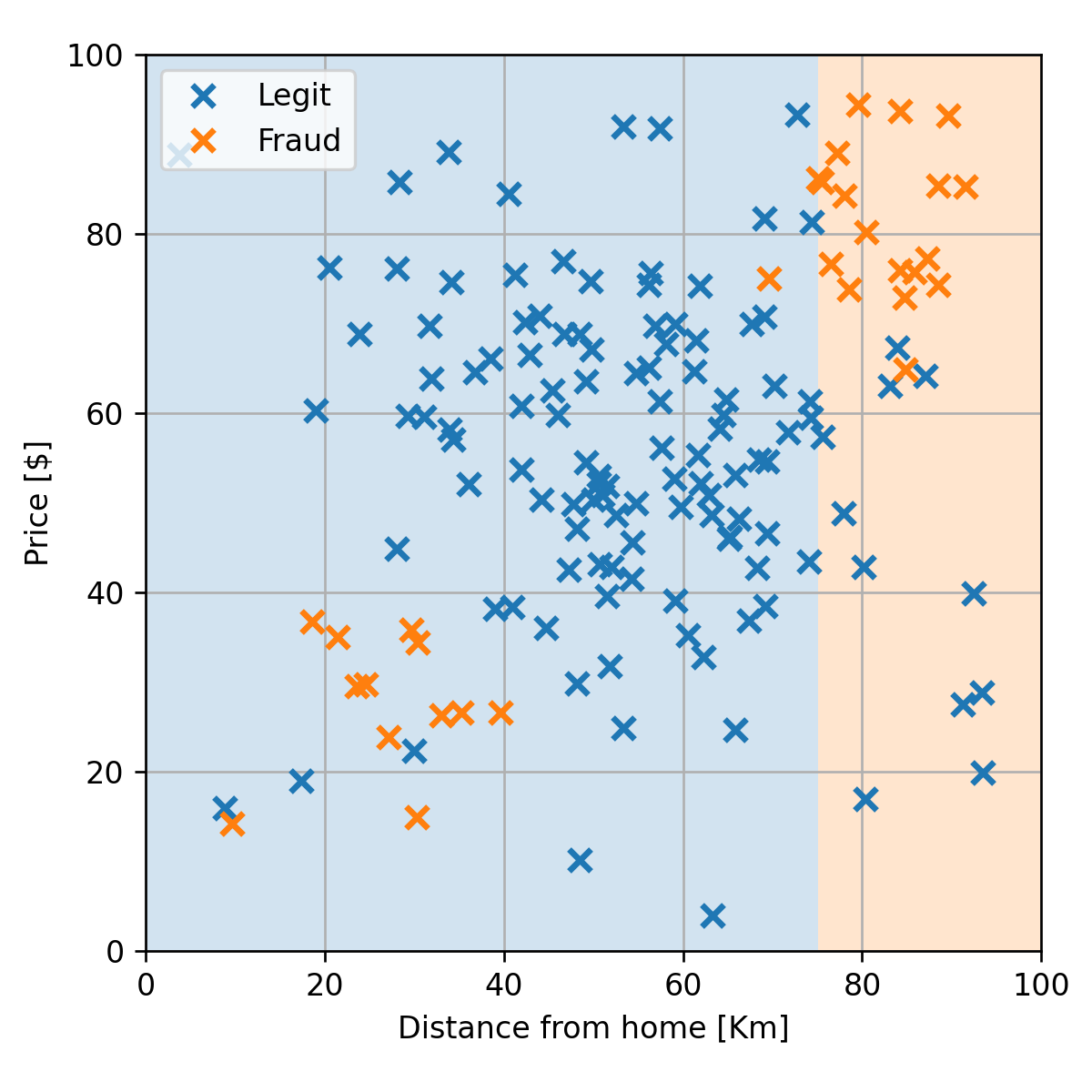
המשך הבניה

נוכל להמשיך כך ולהוסיף צמתים עד אשר נגיע לשגיאה 0 או לעומק מקסימאלי שאותו הגדרנו מראש. אך לפני כן אנו נכניס שינוי קטן באלגוריתם שישפר את ביצועיו.

החלפת המדד

• בדוגמא שהראינו המדד שאותו ניסינו לשפר היה ה misclassification rate.
• מסתבר שניתן לשפר את ביצועי החזאי על ידי החלפה של מדד זה במדד שונה.
• נציג מדדים אלטרנטיבים שמנסים גם להסתכל קדימה ולנסות לשפר את המצב לפיצולים הבאים.

הומגניות והטרוגניות

כדי לקבל בעלה זה מעט שגיאות חיזוי עלינו לדאוג שהפילוג של הדגימות יהיה מרוכז בערך אחד מסויים.

• הומוגניות - המקרה שבו התוויות מרוכזות סביב ערך יחיד (הפילוג טהור - pure).
• הטרוגניות - המקרה שבו התוויות מפולגות בצורה אחידה על פני כל הערכים

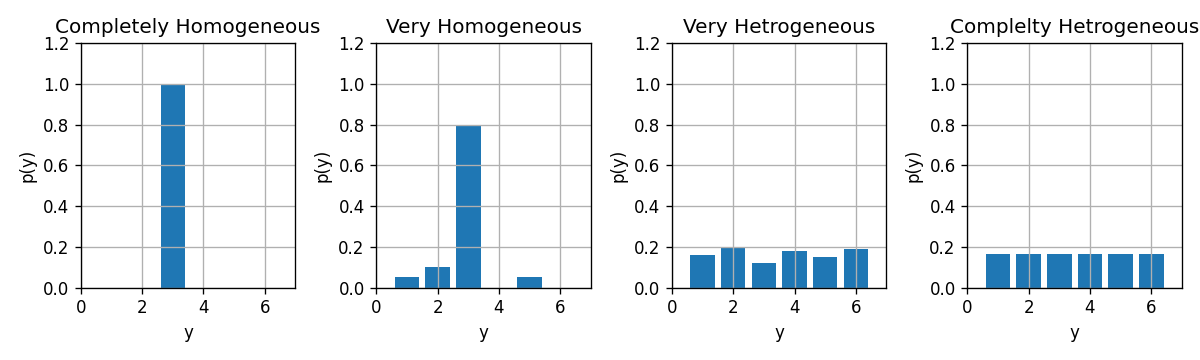
נשאף שהתווית בכל עלה יהיו כמה שיותר הומוגניות.

מדדי חוסר הומוגניות

בהינתן משתנה דיסקרטי מסויים $\text{y}$ בעל פילוג $p(y)$, נגדיר:

• misclassification rate:

  $$Q(p)=1-\max_{y\in\{1,\dots,C\}}p(y)$$

• אינדקס Gini:

  $$Q(p)=\sum_{y\in\{1,\dots,C\}}p(y)(1-p(y))$$

• אנטרופיה:

  $$Q(p)(=H(p))=\sum_{y\in\{1,\dots,C\}}-p(y)\log_2 p(y)$$

המקרה הבינארי

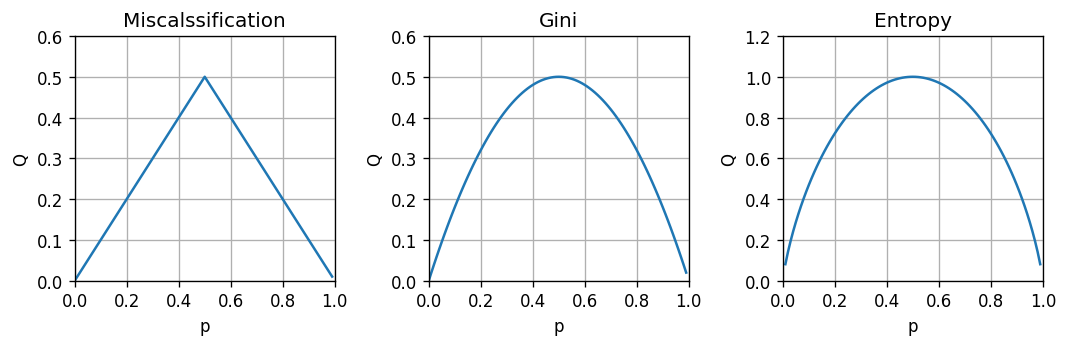
חוסר הומוגניות ממוצעת של עץ

נחשב את חוסר ההומוגניות הממוצעת של עץ באופן הבא:

1. נעביר את המדגם דרך העץ ונפצל אותם לתתי מדגמים.

   • נסמן את האינדקסים של הדגימות בעלה ה $j$ ב $\mathcal{I}_j$.
   • נסמן את כמות הדגימות בעלה ה $j$ ב $N_j$.
2. נחשב את הפילוג של התויות: $\hat{p}_{j,y}=\frac{1}{N_j}\sum_{i\in\mathcal{I}_j} I\{y_i=y\}$
3. נחשב את חוסר ההומוגניות של כל עלה: $Q(\hat{p}_j)$

4. הציון הכולל של העץ יהיה:

   $$Q_{\text{total}}=\sum_j \frac{N_j}{N}Q(\hat{p}_j)$$

כעת נוכל לבנות את העץ תוך נסיון למזער את ממדי השגיאה האלטרנטיבים במקום את ה misclassification rate. לרוב שימוש ב Gini או באנטרופיה יוביל לביצועים טובים יותר.

בחזרה לדוגמא

נחפש שוב את הפיצול האופטימאלי בצומת הראשון בעזרת אינדקס Gini:

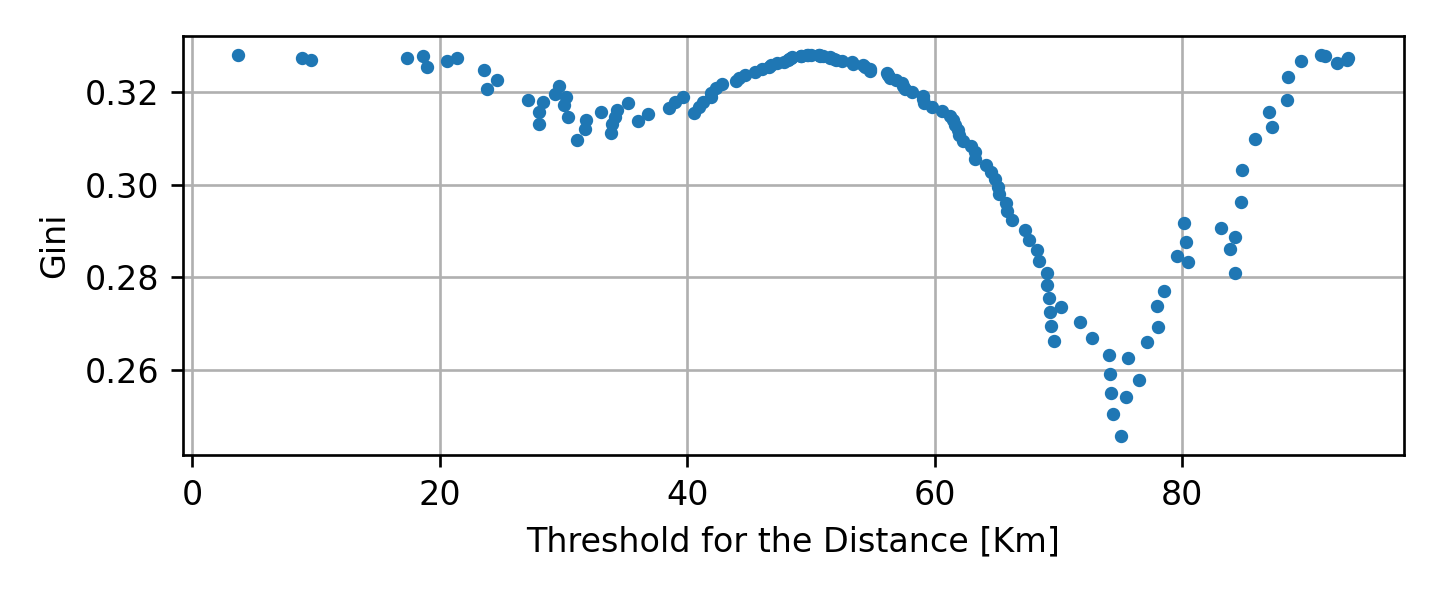
בדומה לקודם, נקבל כי התנאי הטוב ביותר הוא $x_{\text{Distance}}\geq 75$.

הצומת הראשון

לכן הצומת ראשון ישאר:

המשך

נמשיך באותה השיטה ונקבל

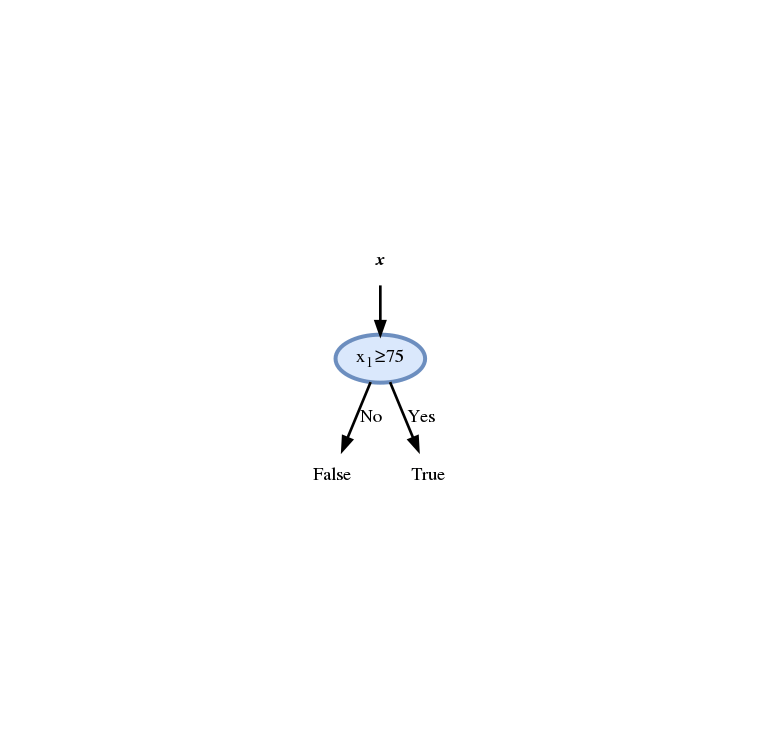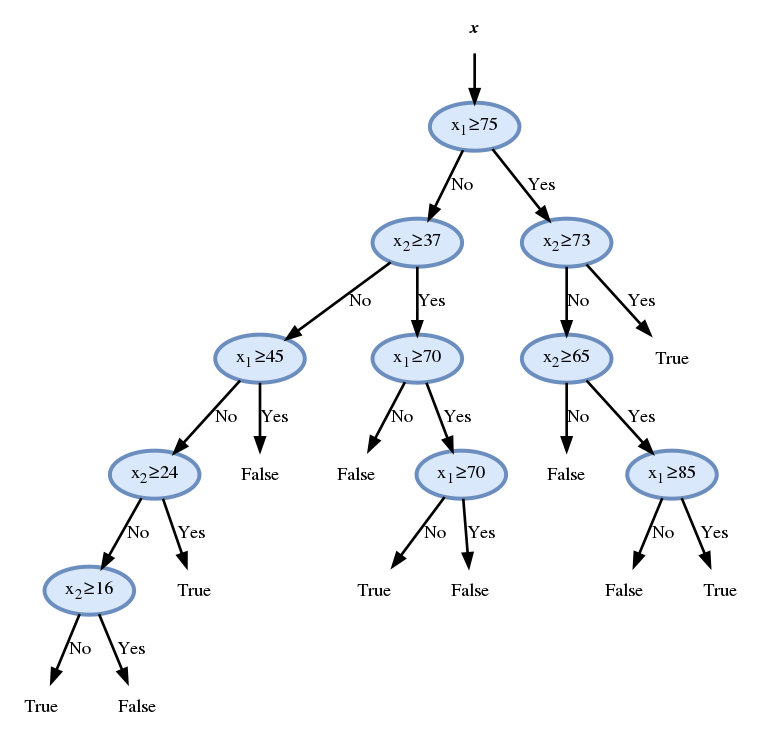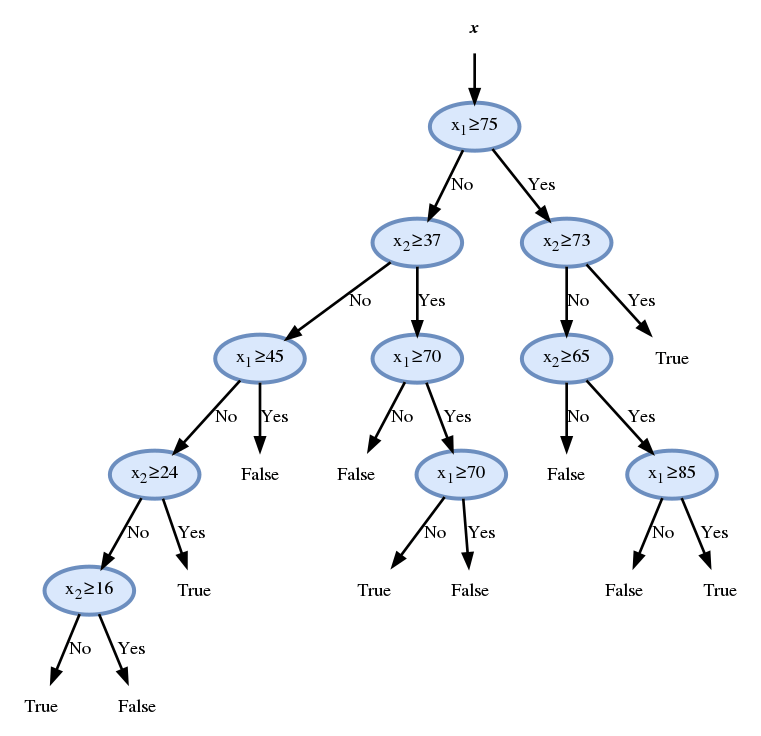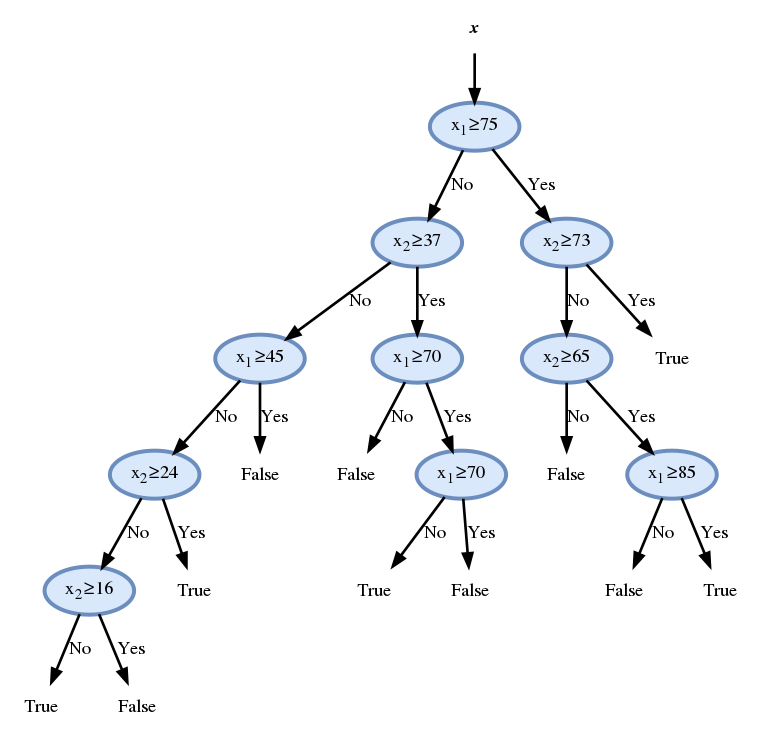
המשך

החזאי לאורך הבניה יראה כך:

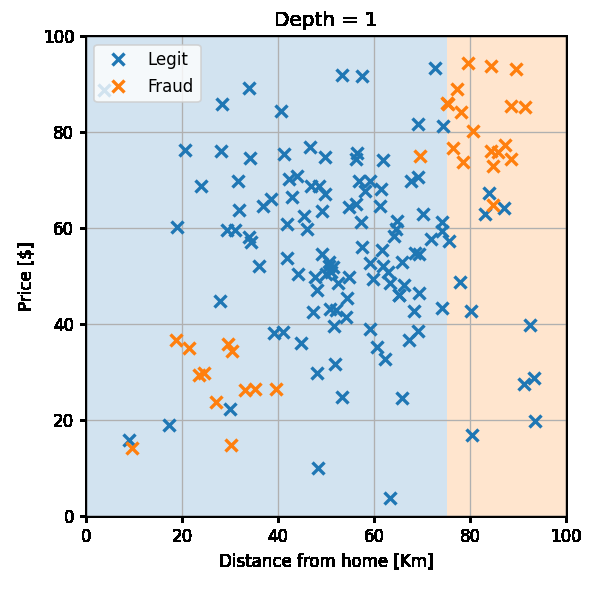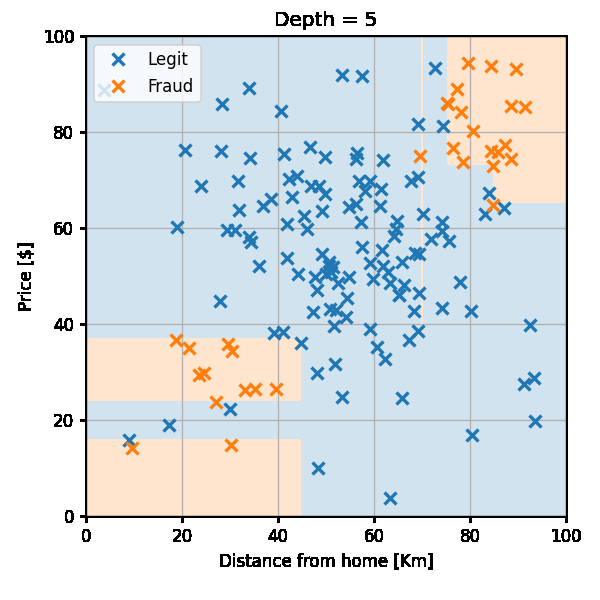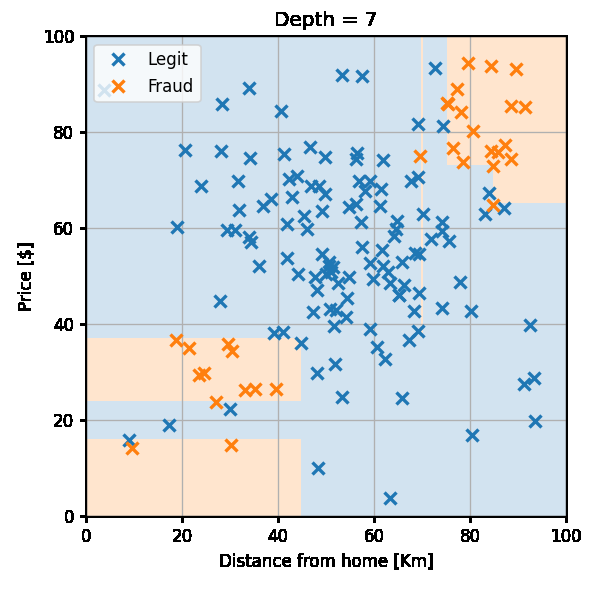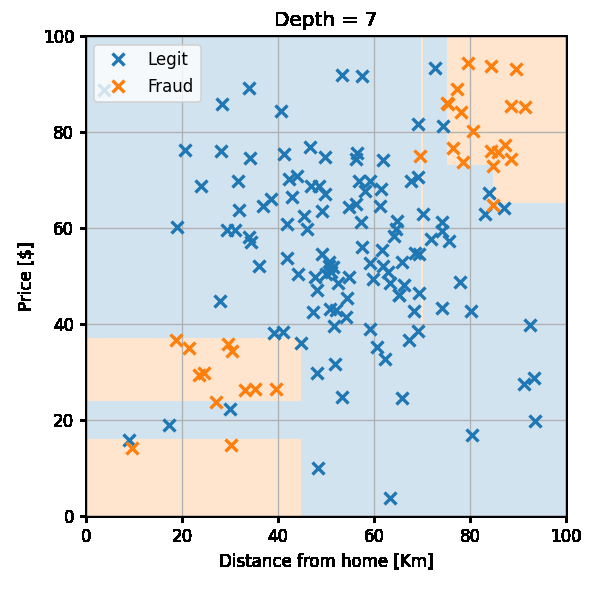
הערכת ביצועים

נבדוק את ביצועי החזאי (עץ בעומק 7) על ה test set:

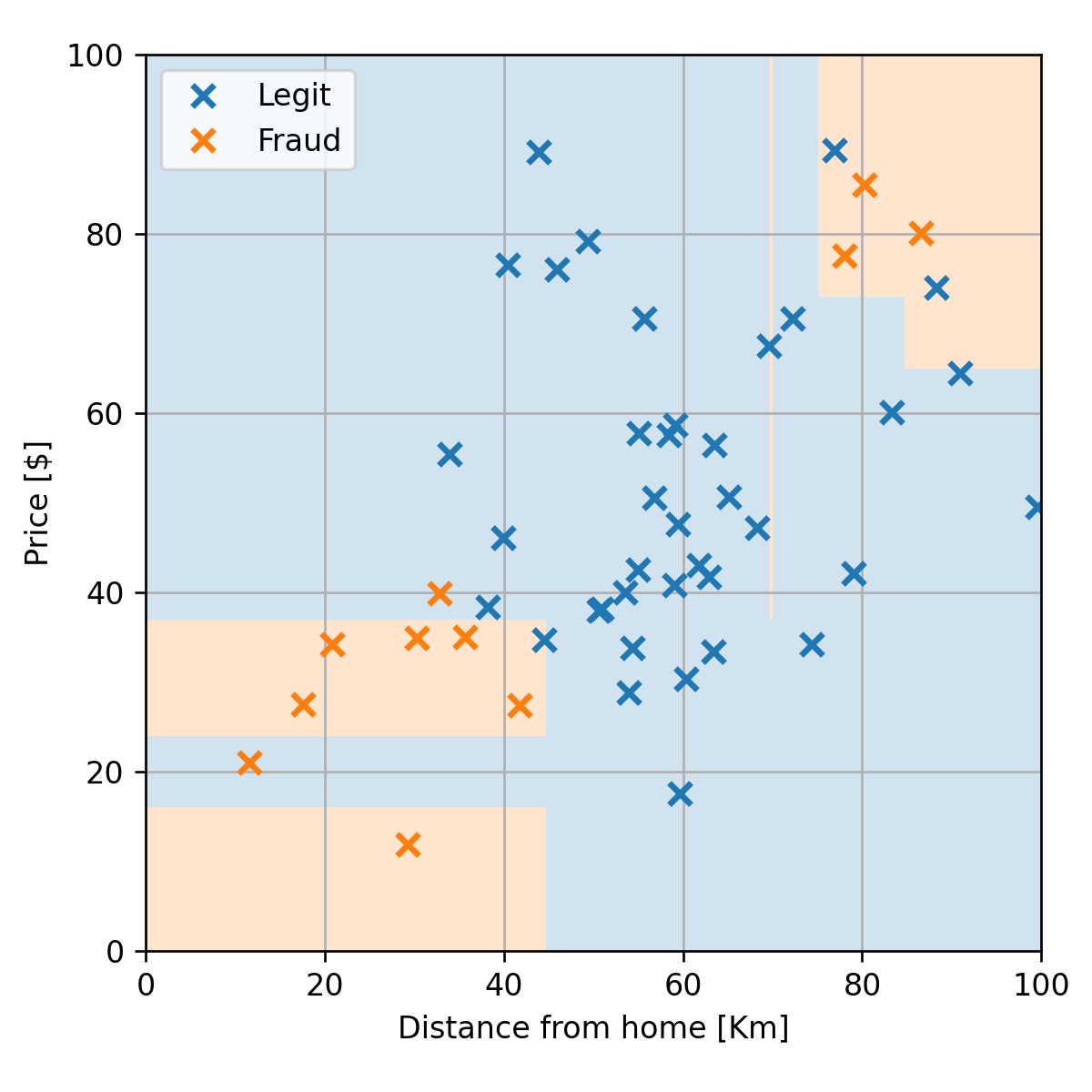
שלב שני - pruning (גיזום)

• אנו נשתמש ב validation set על מנת לאתר ענפים אשר אינם משפרים או פוגעים בביצעי החזאי.
• נעבור על כל הצמתים שבקצוות העץ ננסה להסירם.
• נבדוק את הציון המתקבל על ה validation set איתם ובלעדיהם.
• אם הנוכחות שלהם לא משפרת את ביצועי החזאי נסיר אותם.
• אנו נמשיך ונבדוק את הענפים בקצות העץ עד שלא יישארו צמתים שיש להסיר.

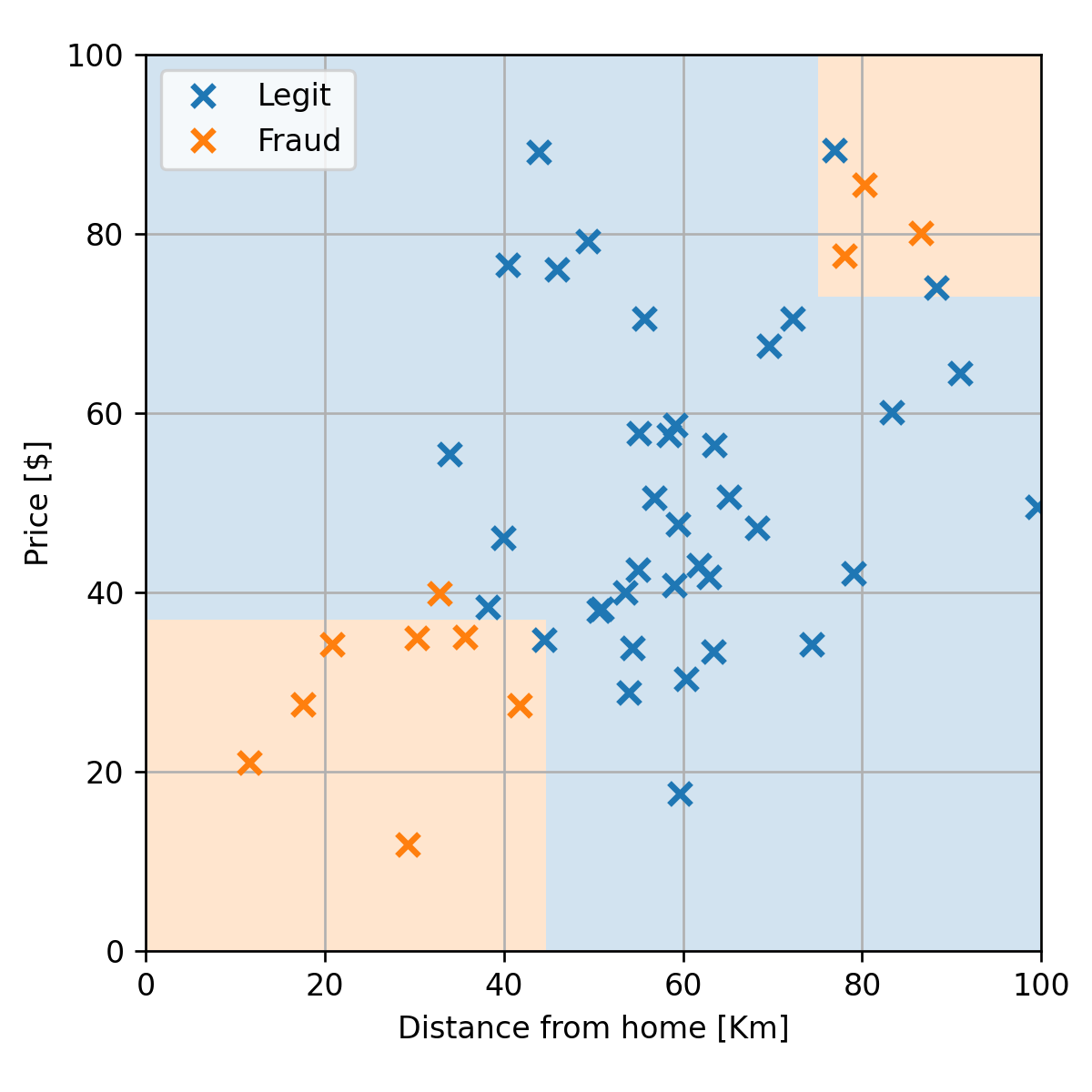
דוגמא

העץ לפני ה pruning הינו:

דוגמא

ואחריו הינו:

הערכת ביצועים

Regression Tree

ניתן להשתמש בעצים גם לפתרון בעיות רגרסיה. במקרה של רגרסיה עם פונקציית מחיר של MSE, הבניה של העץ תהיה זהה מלבד שני הבדלים:

1. תוצאת החיזוי בעלה מסויים תהיה הערך הממוצע של התוויות באותו עלה. (במקום הערך השכיח)

2. את מדד החוסר ההומוגניות נחליף בשגיאה הריבועית של החיזוי של העץ.

Regression Tree

דוגמה לפונקציה קבועה למקוטעין המתקבלת מעצי רגרסיה.

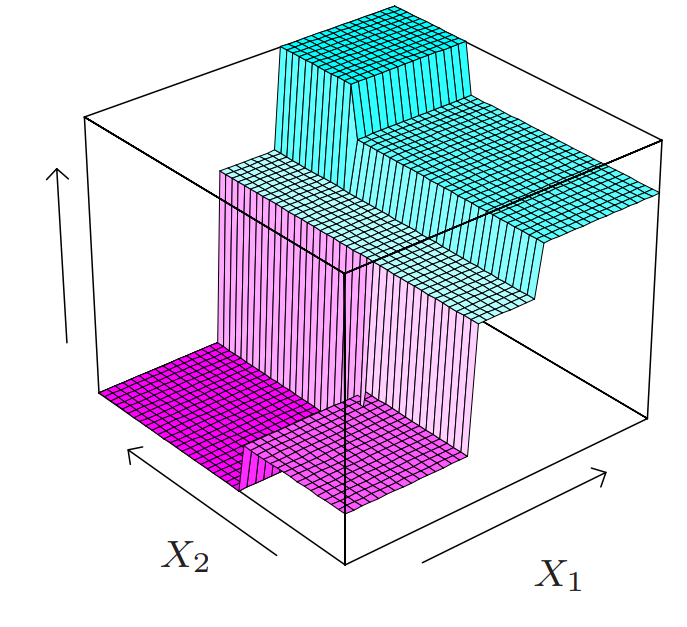
האיור מתוך, James, Witten, Hastie, Tibshirani, Taylor, An Introduction to Statistical Learning, Springer 2023

יתרונות

1. פשטות בהבנת הסיווג (interpretability) - ייצוג גרפי נוח
2. בניית עץ מהירה וסיווג מהיר של נקודות חדשות
3. אין הנחות על טבע הבעיה (למשל סיווג לינארי)
4. גמישות - נתונים מספריים וקטגוריים
5. התאמת יתר נמנעת ע"י תהליך הגיזום

חסרונות

1. חלוקה מקבילה לצירים מוגבלת ומתעלמת מקשרים בין משתנים
2. רגישות גבוהה לשינויים בנתונים (מופחתת עקב גיזום)
3. דרוש מספר רב של נתונים לקבלת תוצאות סבירות

הרחבות

1. העשרת מבנה ההחלטות בצמתים (למשל, מסווג לינארי)
2. שיטות אנסמבל - נדון בהמשך

עצי החלטה מבוססי סיפים חד-ממדיים

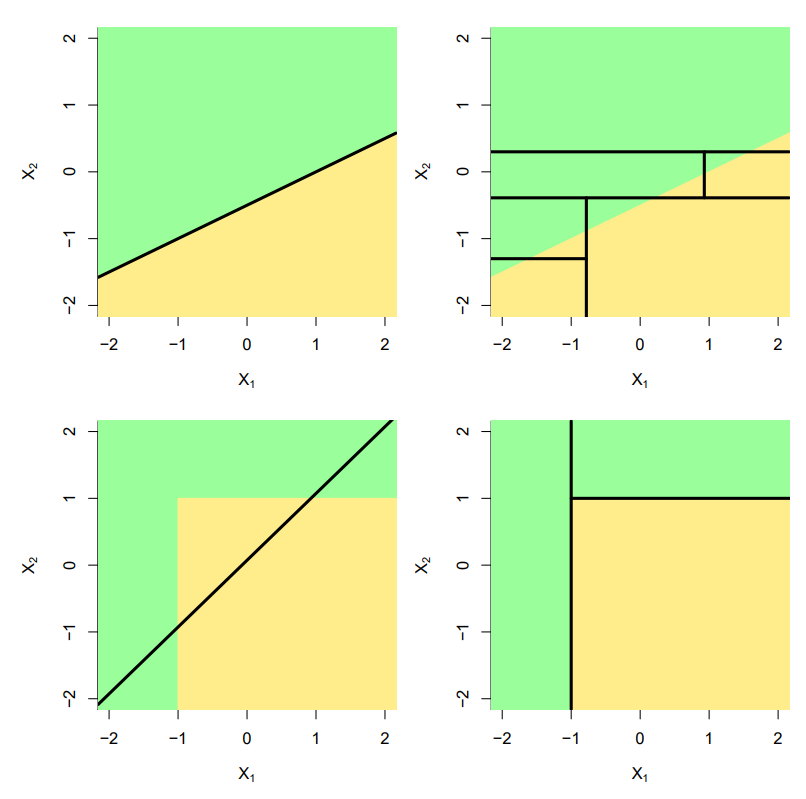
האיור מתוך, James, Witten, Hastie, Tibshirani, Taylor, An Introduction to Statistical Learning, Springer 2023